Определенных интегралов
Определенный интеграл
 (48)
(48)
с пределами интегрирования a и b можно трактовать как площадь фигуры (рисунок 20), ограниченной ординатами a и b, осью абсцисс х и графиком подынтегральной функции f(x).
 |
Рисунок 20 – Графическая интерпретация определенного интеграла
Определенный интеграл, у которого известна его первообразная F(x), вычисляется по формуле Ньютона-Лейбница:
I = F(b) - F(a).
Поэтому достаточно вычислить значения первообразной функции F(x) при x=a и x=b.
Численное интегрирование применяется, если невозможно аналитически записать первообразную F(x) или эта запись имеет очень сложный вид. Оно заключается в замене подынтегральной функции f(x) на отрезке [a; b] аппроксимирующей функцией.
Наиболее распределенными численными методами интегрирования являются: метод прямоугольника, метод трапеций и метод Симпсона [3-5]. Все эти методы являются приближенными.
Метод прямоугольников
Это самый простейший метод.
Идея метода: кривая подынтегральной функции f(x) заменяется ломаной линией, отрезки которой параллельны оси абсцисс.
Отрезок [a; b] разобьем на n равных частей. Расстояние между двумя соседними точками xi и xi+1 обозначим через h - шаг интегрирования. В полученных точках проведем ординаты, которые будут выступать в качестве сторон прямоугольников (рисунок 20). Есть три варианта этого метода.
Рассмотрим случай, когда стороной прямоугольника выступает левая ордината (рисунок 21а). Площадь любого прямоугольника равна
DSi = (xi+1 - xi) f(xi) = h f(xi). (49)
Тогда, значение определенного интеграла будет соответствовать сумме прямоугольников:
 , (50)
, (50)
где h=(b-a)/n - шаг интегрирования;
n - число интервалов разбиения.
Рассмотрим случай, когда стороной прямоугольника выступает правая ордината (рисунок 21б). Тогда, формула для нахождения определенного интеграла примет вид:
 . (51)
. (51)
Выражения (50) и (51) обеспечивают низкую точность значения интеграла. Для того, чтобы интегральная сумма мало отличалась от значения интеграла, число интервалов n должно быть достаточно велико. Для повышения точности также применяют следующее, в качестве стороны прямоугольника принимается ордината, соответствующая середине интервала разбиения (рисунок 21в). Тогда, определенный интеграл равен:
 , (52)
, (52)
где  - середина интервала i.
- середина интервала i.
Погрешность вычисления по методу прямоугольников e» h при h<<1.
 |  |
а б
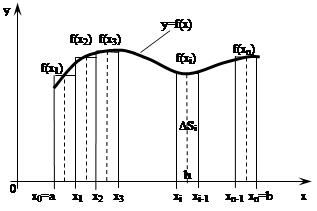 |
в
Рисунок 21 – Графическая интерпретация метода прямоугольников:
а) левых; б) правых; в) средних
Блок-схема алгоритма для вычисления значений определенного интеграла методом средних прямоугольников приведена на рисунке 22.

Рисунок 22 – Блок схема метода средних прямоугольников
Метод трапеций
Идея метода: участок интегрирования [a; b] разбивается на n равных частей. Во всех точках деления проводятся ординаты, и каждая из полученных криволинейных трапеций заменяется прямолинейной трапецией. Тогда приближенной значение интеграла будет равно сумме площадей прямоугольных трапеций (рисунок 23).
При равных значениях шага интегрирования h метод трапеций обеспечивает большую точность, чем метод прямоугольников, поскольку подынтегральная функция f(x) аппроксимируется более точно.
Сторонами трапеции будут две соседние ординаты yi-1 и yi, участок оси ОХ длиной h и хорда кривой, тогда площадь трапеции равна
 . (53)
. (53)
Суммирование выражений (53) на участке интегрирования [a; b] приводит к значению определенного интеграла:
 . (54)
. (54)
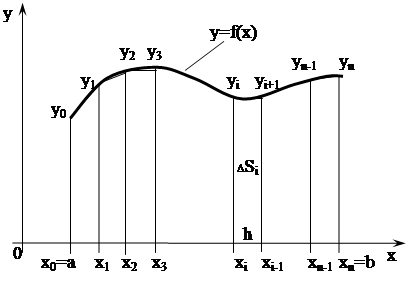 |
Рисунок 23 – Графическая интерпретация метода трапеций
Погрешность интегрирования по методу трапеций при h<<1 составляет e»h2.
Блок-схема алгоритма для нахождения значений определенного интеграла методом трапеций приведена на рисунке 24.
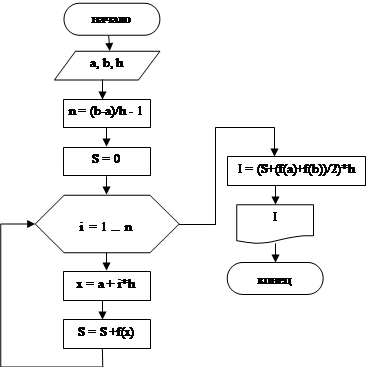
Рисунок 24 – Блок-схема метода трапеций
Метод Симпсона (метод парабол)
Идея метода: подынтегральная кривая f(x) аппроксимируется параболами. Интервал интегрирования [a; b] разбивается на n=2m равных отрезков (их число должно быть четным) (рисунок 25).
На паре соседних отрезков, например, в точке x0=a, кривая y=f(x) заменяется параболой y=ax2+bx+c, коэффициенты которой подбираются так, что она проходит через точки с ординатами y0, y1, y2.

Рисунок 25 – Графическая интерпретация метод Симпсона
Тогда, площадь фигуры, ограниченной параболой можно определить по формуле:
 . (55)
. (55)
Суммируя DSi получим формулу Симпсона для вычисления определенного интеграла:
 . (56)
. (56)
Метод Симпсона дает более точное приближение интегральной суммы к интегралу и при равных значениях шага интегрирования h обеспечивает большую точность, чем методы прямоугольников и трапеций. Погрешность метода при h<<1 составляет e»h3… h4.
Блок-схема алгоритма нахождения значений определенного интеграла методом Симпсона приведена на рисунке 26.
 |
Рисунок 26 – Блок-схема метода Симпсона






