СЫЗЫҚТЫҚ ОПЕРАТОРЛАР» пәнінің дәрістері
КІРІСПЕ
Жиынды түрлендірулердің ішінде шығу және келу облыстары сан жиындары болмайтын түрлендірулердің орны ерекше. Мұндай түрлендірулерді әдетте операторлар деп атайды.
Ұсынылып отырған элективтік курста нақты және комплекс сандар өрістерінде берілген сызықтық кеңістіктер мен евклидтік кеңістіктердің сызықтық операторлары оқылады. Сызықтық операторлар жиынының өзі сы- зықтық кеңістік болатыны, сақина құрайтыны дәлелденеді. Сондай-ақ шекті өлшемді евклидтік кеңістіктегі спектрлар теориясының негізгі мәселелері қарастырылады.
Курстың қысқаша мазмұны:
Сызықтық оператор ұғымы, оның матрица түрінде берілуі. Сызықтық операторлар сақинасының матрицалар сақинасына изоморфтылығы. Сызықтық оператордың характеристикалық көпмүшелігі. Меншікті векторлар мен меншікті мәндер. Жай спектрлі сызықтық операторлар. Сызықтық оператордың матрицасын диагональ түрге келтіру.
Курс мақсаты —студенттерді алгебралық жүйелердің негізгі түрлерімен, соның ішінде, сызықтық кеңістіктермен және оларға қолданылатын сызықтық операторлармен жан-жақты таныстыру; жоғары математиканың әртүрлі салаларының арасындағы байланыстарды нақты мысалдармен түсіндіру; университет курсының төменгі сатысында алған білімдерін күрделі ой қорытулар мен дәлелдемелерге қолдана білуге үйрету; логикалық ойлау мен математикалық сауаттылыққа тәрбиелеу.
Курс міндеті —алгебралар теориясында қалыптасқан ұғымдар мен нәтижелердің ішкі байланыстарын түсінуге, сырттай қарағанда әртүрлі болып көрінетін көптеген алгебралық системалардың арасынан аксиоматикасы ұқсастарын анықтауға, изоморфты болатын-болмайтындарын ажыратуға студенттерді үйрету.
Сызықтық кеңістіктер
n  1. Сызықтық кеңістіктің анықтамасы
1. Сызықтық кеңістіктің анықтамасы
Айталық, V – кезкелген құр емес жиын, ал F – өріс болсын. Өрістің элементтерін грек алфавитінің, ал V жиынының элементтерін латын алфавитінің кіші әріптерімен белгілейміз. F өрісін – скалярлар өрісі дейміз.
V жиынында абстракты түрде «қосу» деп аталатын бір БАО және «скалярға көбейту» деп аталатын бірнеше сыртқы операция берілсін. Нәтижесінде
 V, +,
V, +, 


 F
F 
 алгебрасын аламыз. Оны V деп белгілейміз.
алгебрасын аламыз. Оны V деп белгілейміз.
(Ескерту. Әдетте әріптердің арасына көбейту таңбасын қоймайды!)
Анықтама. Егер V =  V, +,
V, +, 


 F
F 
 алгебрасының операциялары төмендегі аксиомаларға бағынса, онда ол алгебраны F өрісінде берілген сызықтық кеңістік деп атайды:
алгебрасының операциялары төмендегі аксиомаларға бағынса, онда ол алгебраны F өрісінде берілген сызықтық кеңістік деп атайды:
I  а,b
а,b  V a + b = b + a
V a + b = b + a
II  а,b,c
а,b,c  V (a + b) + c = a + (b + c)
V (a + b) + c = a + (b + c)
III 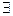 e
e  V
V  а
а  V a + e = a (e –нольдік элемент, оны 0 деп белгілейді)
V a + e = a (e –нольдік элемент, оны 0 деп белгілейді)
IV  а
а  V
V 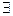 x
x  V a + x = e (x – a- ға қарама-қарсы эл.,оны – a деп белг.)
V a + x = e (x – a- ға қарама-қарсы эл.,оны – a деп белг.)
V  а
а  V
V 
 ,
, 
 F (
F ( ) a =
) a =  (
( a) =
a) =  (
( a)
a)
VI  а
а  V
V 
 ,
, 
 F (
F ( +
+  ) a =
) a =  a +
a +  a
a
VII  а,b
а,b  V
V 

 F
F  (a + b) =
(a + b) =  a +
a +  b
b
VIII  а
а  V 1a = a (1 – F өрісінің бірі) (унитарлық аксиомасы)
V 1a = a (1 – F өрісінің бірі) (унитарлық аксиомасы)
I – IV аксиомалардан V жиыны + -ға қатысты абельдік группа болатыны шығады, яғни  V, +
V, +  – абельдік группа. Ол сызықтық кеңістіктің аддитивті группасы деп аталады.
– абельдік группа. Ол сызықтық кеңістіктің аддитивті группасы деп аталады.
Сызықтық кеңістік ұғымы өте кең ұғым және математиканың барлық салаларында маңызды роль атқарады. Формальды түрде сызықтық кеңістікті векторлық кеңістік деп, ал оның элементтерін векторлар деп атайды.
Егер F өрісі ретінде R – нақты сандар өрісі алынса, онда сызықтық кеңістікті «нақты кеңістік» деп, ал F = C болса, онда – «комплекс кеңістік» деп атайды.
n  2. Векторлық кеңістіктің қарапайым қасиеттері
2. Векторлық кеңістіктің қарапайым қасиеттері
1 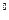 .
.  V, +
V, +  – абельдік группа болғандықтан аддитивті группаның барлық
– абельдік группа болғандықтан аддитивті группаның барлық
қасиеттері векторлық кеңістікте орындалады. Олар: 0 вектор біреу, – a
векторы біреу, қосудың қысқарту заңы ( а,b,c
а,b,c  V (a + b = a + c
V (a + b = a + c 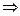 b=c)),
b=c)),
ассоциативтік қасиеттің жалпыламасы, азайту амалы.
Кезкелген а,b  V үшін – b
V үшін – b  Vболғандықтан а + (– b)
Vболғандықтан а + (– b)  V (себ. + - БАО).
V (себ. + - БАО).
Осы а + (– b) элементін а – b деп белгілеп, а мен b элементтерінің айыр-
масы деп атайды. Онда  а,b
а,b  V элементтеріне а – b элементін сәйкес –
V элементтеріне а – b элементін сәйкес –
тікке қоятын амалды азайту амалы деп атайды.
2 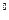 .
.  а,b
а,b  V (a + b = a
V (a + b = a 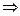 b= 0).
b= 0).
Шынында да, a + b = a болғасын, III аксиомадан a + 0 = a болғандықтан,
a + b = a + 0, онда қосудың қысқарту заңы бойынша, b= 0.
3 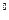 .
.  а
а  V 0a = 0. (мұндағы 0 – F өрісінің нолі)
V 0a = 0. (мұндағы 0 – F өрісінің нолі)
VI VIII
Шынында да, 0a = (1-1) a = 1a - 1a = a – a = 0.
4 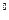 .
. 

 F
F  0 = 0.
0 = 0.
VII III 2 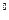
 0 +
0 +  0 =
0 =  (0 + 0) =
(0 + 0) =  0
0 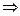
 0 = 0.
0 = 0.
5 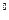 .
.  а,b
а,b  V (a + b = 0
V (a + b = 0 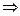 b= – a = (-1) a).
b= – a = (-1) a).
a + b = 0 болса, екінші жағынан IV аксиомадан a +(- a) = 0 екенінен
a + b = a +(-a) болады, онда + -ң қысқ. заң. b= – a немесе b =(-1) a.
6 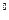 .
.  а,b
а,b  V
V 

 F (
F ( a =
a =  b &
b & 
 0
0 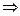 a = b).
a = b).
V VIII
Берілгенінен, 
 (
( a) =
a) = 
 (
( b)
b) 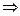 (
(

 ) a = (
) a = (

 ) b
) b 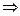 1a =1b
1a =1b 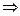
a = b.
7  .
.  а
а  V
V 

 F (
F ( a = 0
a = 0 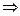
 = 0
= 0  a = 0).
a = 0).
Шынында да,  a = 0 болса,
a = 0 болса,  скаляры үшін екі жағдай болуы мүмкін:
скаляры үшін екі жағдай болуы мүмкін:
 = 0
= 0 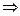 0a = 0 (3
0a = 0 (3 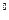 қасиеттен);
қасиеттен);

 0
0 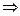 4
4 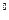 бой.
бой.  0 = 0, онда жоғарыдағымен екеуінен,
0 = 0, онда жоғарыдағымен екеуінен,  a =
a =  0
0 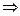 a= 0
a= 0
(6 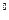 қасиеттен).
қасиеттен).
8 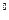 .
.  а
а  V
V 
 ,
, 
 F (
F ( a =
a =  a & a
a & a  0
0 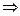
 =
=  ).
).
Берілгенінің екі жағына да (–  a) векторын қосамыз:
a) векторын қосамыз:
 a +(–
a +(–  a) =
a) =  a + (–
a + (–  a)
a) 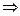 (
( –
–  ) a = 0
) a = 0 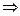 (a
(a  0 болғандықтан, 7
0 болғандықтан, 7 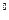 бой.)
бой.)
 –
–  = 0
= 0 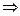
 =
=  .
.
n  3. Векторлық кеңістіктің мысалдары
3. Векторлық кеңістіктің мысалдары
1. F – кезкелген өріс болсын. V жиыны ретінде F  F
F  ...
...  F жиынын
F жиынын
алайық: V = F  F
F  ...
...  F =
F =  <
< 
 ,
, 
 ,…,
,…, 
 >
> 
 i
i 

 F
F  = F
= F 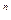 –
–
F өрісінің элементтерінен құралған, ұзындығы n –ға тең кортеждер жиыны.
Бұл жиында кортеждерді қосу, кортежді 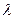 скалярына (
скалярына (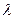
 F) көбейту амал-
F) көбейту амал-
дарының қалай анықталатыны алгебра курсынан белгілі:
< 
 ,
, 
 ,…,
,…, 
 > + <
> + < 
 ,
, 
 ,…,
,…, 
 > = <
> = < 
 +
+ 
 ,
, 
 +
+ 
 ,…,
,…, 
 +
+ 
 >
>
 <
< 
 ,
, 
 ,…,
,…, 
 > = <
> = < 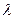

 ,
, 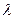

 , …,
, …, 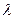

 >
>
Сонда  F
F 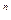 , +,
, +, 


 F
F 
 алгебрасын аламыз. Бұл алгебрада вектор –
алгебрасын аламыз. Бұл алгебрада вектор –
лық кеңістіктің анықтамасындағы I – VIII аксиомалардың орындалатынын
тексеру оңай. Онда бұл алгебра векторлық кеңістік құрайды. Оның нольдік
векторы < 0,0,...,0 > кортежі, ал a = < 
 ,
, 
 ,…,
,…, 
 > векторына қарама –
> векторына қарама –
қарсы вектор – a = < - 
 , -
, - 
 ,…, -
,…, - 
 > кортежі болады. Сонымен,
> кортежі болады. Сонымен,
 F
F 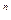 , +,
, +, 


 F
F 
 алгебрасы F өрісінде берілген векторлық кеңістік.
алгебрасы F өрісінде берілген векторлық кеңістік.
Оны n өлшемді арифметикалық векторлық кеңістік деп атайды.
Жеке жағдайлары: F = Q, R, C болғанда Q  , R
, R  , C
, C 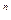 кеңістіктері шығады.
кеңістіктері шығады.
F = R, n = 2 болғанда R  – жазықтық, ал F = R, n = 3 болғанда R
– жазықтық, ал F = R, n = 3 болғанда R  – әдеттегі
– әдеттегі
үш өлшемді кеңістік болады.
2. V жиыны ретінде жазықтықтағы бір О нүктесінен шығатын бағытталған
кесінділер жиынын алайық. Бағытталған кесінділерді параллелограмм
ережесі бойынша қосуға, нақты санға көбейтуге (ол –
кесіндіні ұзарту не қысқарту) болады. Онда бұл екі
амал анықтамадағы I–VIII аксиомаларға бағынатыны
түсінікті. Олай болса, бағытталған кесінділер жиыны
V, нақты сандар өрісінде берілген векторлық кеңістік
құрайды.
Ескерту. Мектепте осы мысал вектор ұғымын енгізудің негізі болады.
3. V = М  (R) – n –ші ретті квадрат матрицалар жиыны болсын. Матрица –
(R) – n –ші ретті квадрат матрицалар жиыны болсын. Матрица –
ларды қосу, матрицаны нақты санға көбейту амалдары I – VIII аксиома –
ларға бағынатынын алгебра курсынан білеміз. Онда бұл алгебра да вектор-
лық кеңістік болады:
 М
М  (R), +,
(R), +, 


 R
R 
 – R– да берілген векторлық кеңістік. Оның
– R– да берілген векторлық кеңістік. Оның
нольдік векторы нольдік матрица, ал a = (
 )
)  векторына (матрицасына)
векторына (матрицасына)
қарама – қарсы вектор – a = (- 
 )
)  қарама – қарсы матрицасы болады.
қарама – қарсы матрицасы болады.
Жеке жағдайы, n = 2 болса 2-ші ретті квадрат матрицалардың нақты кеңіс –
тігі, n = 3 болса 3-ші ретті квадрат матрицалардың нақты кеңістігі болады.
4. V = C – комплекс сандар жиыны болсын. Әдеттегі, комплекс сандарды
қосу, комплекс санды нақты санға көбейту амалдары анықтамадағы I–VIII
аксиомаларға бағынатынын оңай тексере аламыз. Олай болса, комплекс
сандар алгебрасы  C, +,
C, +, 


 R
R 
 – нақты сандар өрісінде берілген
– нақты сандар өрісінде берілген
векторлық кеңістік болады.
5. V – мүшелері нақты сандар болатын тізбектер жиыны болсын:
V = 










 R
R  . Тізбектерді мүшелеп қосатынын, тізбекті
. Тізбектерді мүшелеп қосатынын, тізбекті
нақты санға көбейту үшін оның мүшелерін сол санға көбейтетінін білеміз.
Бұл амалдар жоғарыдағы анықтамадағы I – VIII аксиомаларға бағынады.
Онда бұл жиын да осы амалдар арқылы векторлық кеңістік құрайды.












 R
R  , +,
, +, 


 R
R 
 – R– да берілген векторлық
– R– да берілген векторлық
кеңістік.
6. V –  а,b
а,b  кесіндісінде анықталған үздіксіз функциялар жиыны болсын:
кесіндісінде анықталған үздіксіз функциялар жиыны болсын:
V =  f
f  f – үздіксіз & D(f) =
f – үздіксіз & D(f) =  а,b
а,b 
 = С
= С  . Үздіксіз функцияларды
. Үздіксіз функцияларды
қосу нүктелік қосу, ал үздіксіз функцияны нақты санға көбейту оның әрбір
нүктедегі мәнін сол санға көбейту болады.
Бұлай анықталған амалдар да I–VIII аксиома-
ларға бағынатынын тексеру оңай. Онда бұл
алгебра да нақты сандар өрісінде (яғни, R– да)
берілген векторлық кеңістік болады:
 С
С  , +,
, +, 


 R
R 
 – R– да берілген
– R– да берілген
векторлық кеңістік.
Ішкі кеңістіктер
n  1. Ішкі кеңістіктің анықтамасы, критериі, мысалдары
1. Ішкі кеңістіктің анықтамасы, критериі, мысалдары
Айталық, V =  V, +,
V, +, 


 F
F 
 – векторлық кеңістік, W
– векторлық кеңістік, W  V болсын.
V болсын.
Анықтама. Егер F өрісінде берілген V векторлық кеңістігінің құр емес ішкі
жиыны W векторлық кеңістіктің операцияларынан индуциирленген опера –
циялар арқылы өзі векторлық кеңістік құраса, онда оны ішкі кеңістік деп
атайды. Белгілеуі  ;
;
W =  W, +
W, +  ,
, 



 F
F 

 V.
V.
Теорема (ішкі кеңістіктің критериі). Векторлық кеңістіктің құр емес ішкі жиыны W ішкі кеңістік болуы үшін оның векторлық кеңістіктің операциялары арқылы тұйық болуы қажет және жеткілікті, яғни
W  V
V  а)
а)  а,b
а,b  W a + b
W a + b  W
W
б)  а
а  W
W 

 F
F  a
a  W
W
Дәлелдеу. Қажеттігі. Индуциирленген амалдың анықтамасынан а), б) шарт – тары автоматты түрде шығады.
Жеткіліктігі. W ішкі жиыны а), б) шарттарын қанағаттандырса, яғни тұйық болса, оның өзі векторлық кеңістік болатынын дәлелдеу үшін анықтамадағы
I–VIII аксиомалардың орындалатынын тексеру керек. I,II, V-VIII аксиомалар универсал аксиомалар болғандықтан, олардың орындалатыны түсінікті. III,IV аксиомаларды ғана тексерсе болғаны (студенттердің өздеріне).
Мысалдар.
1). Кезкелген векторлық кеңістіктің екі қарапайым ішкі кеңістігі (тривиальные подпространства) әруақытта белгілі. Олар V -ңөзі және  0
0  .
.
2). F 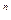 – n өлшемді арифметикалық векторлық кеңістіктің, мысалы,
– n өлшемді арифметикалық векторлық кеңістіктің, мысалы,
W =  < 0,
< 0, 
 ,…,
,…, 
 >
> 
 i
i 

 F
F  түріндегі ішкі жиыны ішкі кеңістік болады (а), б) шарттарын тексеріп көріңіз).
түріндегі ішкі жиыны ішкі кеңістік болады (а), б) шарттарын тексеріп көріңіз).
Жеке жағдайы, R 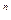 кеңістігін алайық. W ішкі жиыны ретінде n айнымалылы біртекті сызықтық теңдеулер жүйесінің шешулерінің жиынын алайық. Біртекті СТЖ –ң кезкелген екі шешуінің қосындысы да, кезкелген шешудің нақты санға көбейтіндісі де сол жүйенің шешуі болатындығынан бұл жиынның ішкі кеңістік болатыны шығады.
кеңістігін алайық. W ішкі жиыны ретінде n айнымалылы біртекті сызықтық теңдеулер жүйесінің шешулерінің жиынын алайық. Біртекті СТЖ –ң кезкелген екі шешуінің қосындысы да, кезкелген шешудің нақты санға көбейтіндісі де сол жүйенің шешуі болатындығынан бұл жиынның ішкі кеңістік болатыны шығады.
Осы мысалдың тағы бір жеке жағдайын, әдеттегі үш өлшемді R  кеңістігін алайық. W – координаталар бас нүктесі арқылы өтетін жазықтықтың немесе түзудің бойында жататын векторлар (бағытталған кесінділер) жиыны болсын. Онда W ішкі жиыны қосу және нақты санға көбейту арқылы тұйық болатыны түсінікті. Онда ол R
кеңістігін алайық. W – координаталар бас нүктесі арқылы өтетін жазықтықтың немесе түзудің бойында жататын векторлар (бағытталған кесінділер) жиыны болсын. Онда W ішкі жиыны қосу және нақты санға көбейту арқылы тұйық болатыны түсінікті. Онда ол R  кеңістігінің ішкі кеңістігі. Ол сәйкес, R
кеңістігінің ішкі кеңістігі. Ол сәйкес, R  немесе R
немесе R  .
.
3). Мектептен белгілі, жазықтықтағы бір О нүктесінен шығатын бағытталған
кесінділер кеңістігі берілсін (§1, 2 мысал).
W – сол О нүктесі арқылы өтетін l түзуі
болса, онда ол ішкі кеңістік болады. (Неге?)
4).  М
М  (R), +,
(R), +, 


 R
R 
 – n –ші ретті квадрат матрицалар кеңістігінің ішкі жиыны W – үшбұрышты матрицалар жиыны Т
– n –ші ретті квадрат матрицалар кеңістігінің ішкі жиыны W – үшбұрышты матрицалар жиыны Т  (R) болсын. Ол да ішкі кеңістік болады. (Қалайша?)
(R) болсын. Ол да ішкі кеңістік болады. (Қалайша?)
Ескерту. Жалпы, векторлық кеңістіктің ішкі кеңістігін табу мәселесі оңай шаруа емес.
n  2. Векторлар жүйесінің сызықтық қабықшасы
2. Векторлар жүйесінің сызықтық қабықшасы
(линейная оболочка системы векторов)
V =  V, +,
V, +, 


 F
F 
 – F өрісінде берілген векторлық кеңістік, ал
– F өрісінде берілген векторлық кеңістік, ал
а  , а
, а  ,..., а
,..., а 
 V (1) векторлар жүйесі болсын.
V (1) векторлар жүйесі болсын.
Анықтама. b =  а
а  +
+  а
а  +... +
+... +  а
а  векторы (
векторы (
 F) (1) жүйенің сызықтық комбинациясы деп аталады. Кейде, b векторы (1) жүйе арқылы сызықтық өрнектеледі деп те айтады.
F) (1) жүйенің сызықтық комбинациясы деп аталады. Кейде, b векторы (1) жүйе арқылы сызықтық өрнектеледі деп те айтады.
Анықтама. (1) векторлар жүйесінің сызықтық комбинациясы болатын векторлар жиыны сол (1) жүйенің сызықтық қабықшасы деп аталады. Белгілеуі L(а  , а
, а  ,..., а
,..., а  ). Сонда
). Сонда
L(а  , а
, а  ,..., а
,..., а  ) =
) =  х
х  х =
х =  а
а  +
+  а
а  +... +
+... +  а
а  &
& 
 F
F  .
.
Лемма. Векторлар жүйесінің сызықтық қабықшасы векторлық кеңістіктің ішкі кеңістігі болады.
Дәлелдеу. Ішкі кеңістіктің критериі бойынша, а), б) шарттарын тексереді.
(студенттердің өздеріне).
Анықтама. L(а  , а
, а  ,..., а
,..., а  ) ішкі кеңістігін а
) ішкі кеңістігін а  , а
, а  ,..., а
,..., а  векторлар жүйесіне тұрғызылған ішкі кеңістік деп атайды; ал а
векторлар жүйесіне тұрғызылған ішкі кеңістік деп атайды; ал а  , а
, а  ,..., а
,..., а  векторларының өзін осы ішкі кеңістіктің жасаушы элементтері дейді.
векторларының өзін осы ішкі кеңістіктің жасаушы элементтері дейді.
Сұрақ. а  , а
, а  ,..., а
,..., а  векторларының әрқайсысы L(а
векторларының әрқайсысы L(а  , а
, а  ,..., а
,..., а  ) ішкі кеңістігіне тиісті ме? Жауабыңызды дәлелдеңіз.
) ішкі кеңістігіне тиісті ме? Жауабыңызды дәлелдеңіз.
Ескерту. Сонда, векторлық кеңістіктің ішкі кеңістігін табу үшін, оның қандайда бір векторларын алып, солардың сызықтық комбинацияларының жиынын алса болғаны.
n  3. Ішкі кеңістіктерге амалдар қолдану
3. Ішкі кеңістіктерге амалдар қолдану
V – F өрісінде берілген векторлық кеңістік, W  ,W
,W  –ішкі кеңістіктері болсын.
–ішкі кеңістіктері болсын.
Анықтама. W  ,W
,W  ішкі кеңістіктердің қимасы деп
ішкі кеңістіктердің қимасы деп
W 
 W
W  =
=  х
х  V
V  х
х  W
W  & х
& х  W
W 
 жиынын айтады.
жиынын айтады.
Лемма. W 
 W
W  жиыны ішкі кеңістік болады. (Дәлелдеу өзбетімен).
жиыны ішкі кеңістік болады. (Дәлелдеу өзбетімен).
Тұжырымдалған лемма ішкі кеңістіктердің кезкелген жиыны үшін де дұрыс, яғни  i
i  IW
IW  –ішкі кеңістік
–ішкі кеңістік 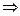
 W
W  –ішкі кеңістік.
–ішкі кеңістік.
i  I
I
Анықтама. W  ,W
,W  ішкі кеңістіктердің қосындысы деп
ішкі кеңістіктердің қосындысы деп
W  + W
+ W  =
=  х
х  V
V  х = а
х = а  + а
+ а  & а
& а 
 W
W  , а
, а 
 W
W 
 жиынын айтады.
жиынын айтады.
Лемма. W






