Определение влагосодержания сероводородсодержащих газов

Для более точного определения влагосодержания сероводородсодержащего природного газа при содержании сероводорода до 50% мольных долей и давлении до Р=70 МПа и температуре 10≤Т≤175 ⁰С необходимо использовать следующий метод: Сначала определить влагосодержание несернистого газа (углеводородные компоненты газа) из рисунка 2.19б; Затем определить мольное содержание в процентах эквивалентной концентрации сероводорода Н₂S в сернистом газе из равенства Н₂S_экв=Н₂S+0,7·СО₂, в %; Далее для заданной величины температуры Т и рассчитанному значению эквивалентной концентрации сероводорода в газе Н₂S_экв, используя кривые, показанные на рисунке 2.19б (см. последовательность нахождения относительного влагосодержания сероводородсодержащего газа к влагосодержанию несернистого газа) находят . Для этого необходимо для известной величины температуры горизонтальной линией пересечь кривую Н₂S_экв, а затем из точки пересечения провести вертикальную линию до пересечения с кривой давления, при котором требуется определить влагосодержание сернистого газа. Из точки пересечения вертикальной линии с кривой давления провести горизонтальную линию до оси ординат с относительным влагосодержанием сернистого газа. Ключ к получению ответа о влагосодержании сернистого газа показан на рисунке 2.19б. Из приведенных результатов видно, что с увеличением сероводорода в газе влагосодержание увеличивается.

 

Рисунок 2.19б - Номограмма для определения относительного влагосодержания сернистого газа.

 

 

Теплоемкость газа (РИС 71-82)

Теплоемкость газа – это отношение количества теплоты, подведенной к газу в заданном термодинамическом процессе, к соответствующему изменению его темпера­туры. В зависимости от вида процесса различают изобарную теплоемкость С_р, когда процесс происходит при постоянном давлении Р=const, и изохорную С_v, когда процесс происходит при постоянном объеме V=const. Единица измерения теплоемкости Дж/кг∙град или Дж/моль·град. Обычно в расчетах используют удельные – массовые или молярные – теплоемкости, т.е. теплоемкости, отнесенные к единице массы или к одному молю газа. Теплоемкость природных газов зависит от давления, температуры и состава газа, а также от процесса передачи тепла. Теплоемкость газа при заданных давлении и температуре определяется как сумма теплоемкостей, состоящих из тепло­емкости при заданной температуре и атмосферном давлении 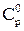и приращения теплоемкости за счет влияния давления ΔС_р, т.е.

(2.54)

Так как 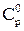– =R, получим:

C_p–C_v=ΔC_р–ΔC_v+R (2.55)

 

 

Теплоемкость газов 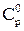при атмосферном давлении определяется графически из рисунка 2.20 или аналитическим путем. При определении теплоемкости газовой смеси известного состава используют формулу:

(2.56)

где – коэффициент теплоем­кости i-го компонента при Р=0,098 МПа, и заданной температуре; g_i – массовая доля i-го компонента в сме­си.

Значения С_р приведены в таблице 2.2 при нормальных условиях и показаны на рисунке 2.20 в интервале изменения температуры 223≤Т≤423 К. Аналитически величина может быть определена по формуле:

=E_i+nF_i+n²G_i+n³Н_i+N_i/n (2.57)

где E_i, F_i, G_i, Н_i, N_i – коэффициенты, определяемые из таблицы 2.10, n=T/100; Т – температура газа, К.

 

 

Изобарная массовая теплоемкость может быть определена по формуле: при 1,6£ Т_пр £ 2,1 и 0,8£ Р_пр £ 3,5, по формулам

,

Рисунок 2.20 – Зависимость изобарной моляр­ной теплоемкости С_р газов при атмосферном давлении от температуры.

 

Теплоемкость газов, не содержащих кислых компонентов и азота при атмосферном давлении, можно определить по известной плотности, используя формулу:

(2.58)

Таблица 2.10 – Коэффициенты уравнения (2.57) для определения С_р⁰, Дж/кг·град

Компоненты	Молекулярная масса, кг/кмоль	, Дж/кг·град	, Дж/кг·град	, Дж/кг·град	, Дж/кг·град	, Дж/кг·град
Метан	16,04		58522,25	15215,04	-2947,67	18575,95
Этан	30,07		62557,49	25663,79	36001,45	3343,11
Пропан	44,09		66328,12	32767,24	62295,40	-782,07
Бутан	58,12		65812,73	33182,44	33182,44	3,8610
Изобутан	–		68152,31	36790,16	75903,33	-1685,56
Пентан	72,15		65762,49	33814,98	66951,12	-112,122
Изопентан	–		66,838,91	34687,09	69556,98	-1530,40
Гексан	86,18		66060,17	34773,68	70914,34	-456,22
Гептан	100,20		66040,07	35091,50	31839,23	-503,65
Октан	114,22		66094,50	35466,84	73861,01	-561,57
Нонан	128,26		65986,06	35489,58	74039,37	-522,39
Декан	142,29		65991,50	-35677,77	74788,39	-549,49
Кислород	32,0		21621,09	16458,14	49445,62	12051,12
Водород	2,02		330368,33	294527,51	14165,32	200717,79
Вода	18,02		40147,27	27801,52	79225,56	26409,75
Гелий	4,0	5191,632
Аргон	39,95	520,712
Криптон	83,80	248,696
Хлор. водород	36,46	741,248	14447,19	187,48	51,33	313,63
Сероводород	64,86		19097,88	154,95	43953,78	5109,53
Двуокись серы	34,08		24379,36	16676,57	45818,66	11682,30
Азот	28,01		21745,15	16129,31	45183,53	15429,99
Двуокись углерода	44,01		25745,76	19428,01	53589,36	6924,42
Окись углерода	28,01		22065,65	16193,91	44592,35	15197,54

 

где B₁÷B₆ – постоянные коэффициенты и соответственно равны: B₁=5,5967; В₂=-2,2335; В₃=0,8073; В₄=-1,0039; В₅=3,1416; В₆=5,7587.

При известном составе газа и наличии H₂S, CO₂ и N₂ теплоемкость при задан­ной температуре и атмосферном давлении может быть определена по форму­ле:

(2.59)

где 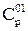– теплоемкость газа без двуокиси углерода, сероводорода и азота, опре­деляемая по формуле (2.58); , , – поправки на присутствие этих компонентов, значения которых определяются по формулам:

(2.60)

(2.61)

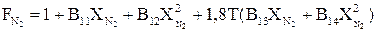(2.62)

где X_i – мольные доли СО₂, H₂S и N₂ в газе; Т – заданная температура, К; В₇÷B₁₄ – постоянные коэффициенты, значения которых соответственно равны: В₇=0,4259 В₈=1,2432·10^-3; В₉=-0,0406; В₁₀=1,0089·10^-3; В₁₁=0,3624; В₁₂=-0,4661; В₁₃=0,0976; В₁₄=0,2708.

Формула (2.59) может быть использована для расчета C_р в диапазоне изменения температуры 273≤T≤423 К и при концентрациях в газе сероводорода до 40%, двуокиси углерода до 20% и азота до 25% (мольных).

Приращение изобарной теплоемкости ΔС_Р может быть определено графическим и аналитическим способами. Наиболее простым способом определения величины ΔС_Р является графический способ по известным приведенным параметрам Р_пр, Т_пр из рисунка 2.21. Для заданного состава газа по известным критическим параметрам каждого компонента Р_кр.i и Т_кр.i по формуле (2.3) определяют псевдокритические параметры газа, а затем приведенные Р_пр=Р/Р_п.кр и Т_пр=Т/Т_п.кр. По известным Р_пр и Т_пр из рисунка 2.21 определяют ΔС_р.

Рисунок 2.21 – Зависимость приращения изобарной теплоемкости ΔС_Р от приведенных давления и темпера­туры.

 

Использование этого способа целесообразно при составе газа, где содержание метана ≥98%. Если мольная концентрация высококипящих углево­дородных и неуглеводородных газов превышает 10%, а также при наличии в газе полярных веществ при определении ΔС_р следует учесть влияние третьего парамет­ра – фактора ацентричности молекул ω. Значение фактора ацентричности вычисля­ется по известному составу газа по формуле (2.22). При известных значениях Р_пр, Т_пр и ω приращение изобарной теплоемкости ΔС_р определяется по формуле:

(2.63)

Значения и определяются графически из рисунков 2.22 и 2.23. Размерность вели­чины ΔС_р зависит от размерности газовой постоянной R. В большинстве случаев используют значение R=1,986 ккал/моль·град. В этом случае для получения тепло­емкости в Дж/моль·град вычисленный результат умножают на 4186,8. Для получения теплоемкости в Дж/кг·град необходимо величину ΔС_Р разделить на молекулярную массу газа М.

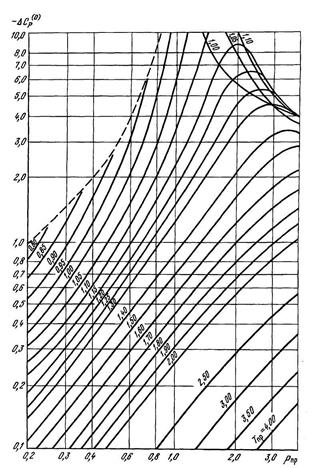
Рисунок 2.22 – Зависимость поправочной функции –ΔС⁽⁰⁾_р от приведенных давления и температуры.

В интервалах изменения приведенных давления 0≤Р_пр≤6 и температуры 1≤Т_пр≤4 величины /R и /R могут быть определены графически из рисунка 2.24. Для более высоких давлений значение ΔС_р может быть определено аналитическим путем. В частности, ΔС_р может быть рассчитана по приведенной форме уравнения Бенедикта-Вебба-Рубина согласно [18].

Для определения изохорной теплоемкости C_v можно использовать фор­мулу:

C_v=C⁰_р+ΔC_v–R (2.64)

где ΔC_v – приращение изохорной теплоемкости, определяемое по формуле:

ΔC_v/R= /R+ /R. (2.65)

Рисунок 2.23 – Зависимость поправочной функции –ΔС⁽¹⁾_р от приведенных давления и температуры.

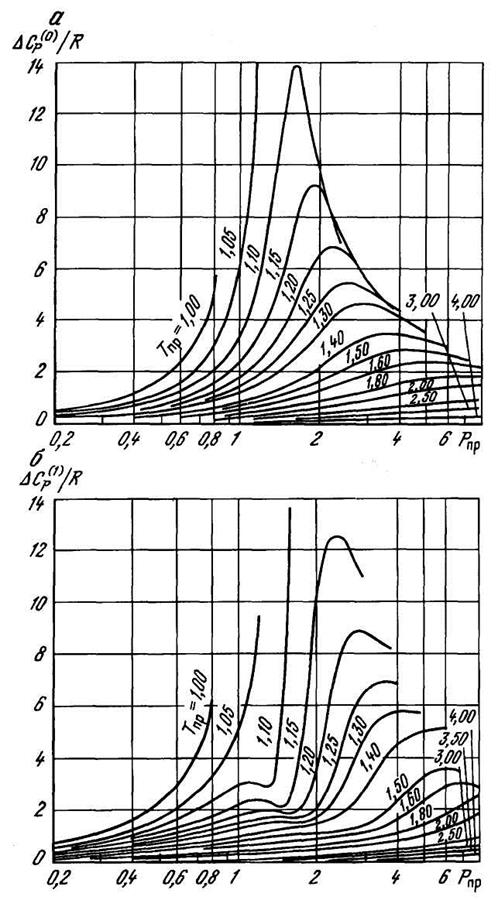
Рисунок 2.24 – Зависимости ΔС⁽⁰⁾_р/R (а) и ΔС⁽¹⁾_р/R (б) от приведенных давления и температуры.

Значения /R и /R находят из рисунка 2.25.

Рисунок 2.25 – Зависимости ΔC_v⁽⁰⁾/R (а) и ΔC_v⁽¹⁾/R (б) от приведенных давления и температуры.

Теплопроводность газа (РИС 82-87)

Теплопроводность газа – это количество тепла, проходящего через его массы без перемещения, конвекции и теплообмена. Количество передаваемого тепла в газовой среде пропорционально градиенту температуры Δt, площади передачи F, продолжитель­ности процесса теплопередачи τ, толщины слоя газа ΔL и выражается формулой:

Q=λ∙F∙τ∙Δt/ΔL (2.66)

где Δt=t₂–t₁ – разность температуры по обе стороны газовой среды толщиной ΔL; λ – коэффициент пропорциональности между количеством тепла и параметрами газовой среды.

Количество тепла, проходящего через единицы площади и толщины за единицы времени при разности температур, равной 1 град, принято называть коэффициентом теплопроводности. Коэффициент теплопроводности измеряется в Дж/м·с·град или Вт/м·град.

Теплопроводность газов зависит от давления, температуры и состава газа и опре­деляется графическим или аналитическим методами. Все аналитические выражения для определения коэффициента теплопроводности получены аппроксимацией экспе­риментальных кривых. Наиболее простым способом определение λ является исполь­зование графических зависимостей λ/λ_ат и λ/λ_кр от приведенных давления и темпе­ратуры, показанных на рисунках 2.26 и 2.27, или зависимости (λ–λ_ат) от приведенной плот­ности ρ_пр, показанной на рисунке 2.28. Для определения λ с использованием рисунка 2.27 необ­ходимо вычислить величину λ_кр, т.е. теплопроводность газа при критических Р_кр и T_кр.

Рисунок 2.26 – Зависимость приведенной теплопроводности λ/λ_ат газов от приведенных давления и температуры – 0,6≤Р_пр≤6 (a) и 0,1≤Р_пр≤1 (б).

 

Для газовых смесей λ_кр должна быть определена как псевдокритическая тепло­проводность по формуле:

λ_пк=12,24·10^-5M_см^0,5Р_п.кр^2/3/Т_п.кр^1/6 (2.67)

где М_см – молекулярная масса смеси, определяемая по формуле:

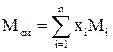(2.68)

где Р_п.кр и Т_п.кр – псевдокритическое давление и температура.

Рисунок 2.27 – Зависимость приведенной теплопроводности λ/λ_кр газов от приведенных давления и температуры.

Рисунок 2.28 – Зависимость Δλ=λ–λ_ат от приведенной плотности газов

 

При использовании рисунков 2.26 и 2.28 для определения λ необходимо вычислить величину λ_ат, т.е. коэффициент теплопроводности при заданной температуре и атмосферном давлении Р_ат=0,098 МПа. Величину λ_ат.см можно определить несколькими расчетными методами.

С погрешностью до 5% значение λ_ат.см может быть определено по формуле:

(2.69)

Величина λ_ат.i в формуле (2.69) определяется в зависимости от заданных темпера­турных условий и состава газа из рисунка 2.29, по табличным данным или расчетным путем. В частности:

– для метана, нафтеновых и ароматических углеводородов при Т_пр<1

; (2.70)

– для остальных углеводородов при любых температурах

(2.71)

– для неуглеводородных компонентов при Т_пр<1

(2.72)

- для неуглеводородных компонентов при 1≤Т_пр≤3

(2.73)

– для неуглеводородных компонентов при 3≤Т_пр≤15

(2.74)

где – теплоемкость i-го компонента при Р_ат; Z_кр.i – значение коэффициента сверхсжимаемости Z при критических параметрах i-го компонента Р_кр.i и Т_кр.i; Т_пр.i – приведенная температура i-го компонента.

Параметр ξ_i и ξ_см определяются по формулам:

; (2.75)

В формулах (2.70)÷(2.74) измеряется в Дж/моль∙град, Р – в МПа, Т – в К и λ – в Вт/м∙град. Более точно значения λ_ат.см и λ могут быть определены согласно [18].

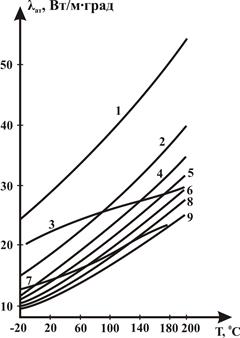
Рисунок 2.29 – Зависимость теплопроводности компонентов природных газов λ_ат при атмосферном давлении от температуры:

1÷9 теплопроводность газов при Р_ат: 1 – метана, 2 – этана, 3 – азота, 4 – пропана, 5 – n-бутана, 6 – n-пентана, 7 – углекислого газа, 8 – n-гексана, 9 – n-гептана.

 

Дросселирование газа. Коэффициент Джоуля-Томсона. (РИС 87-91)

Дросселирование – расширение газа при постоянной энтальпии в процессе его прохождения через сужающие устройства (т.е. через местное сопротивление, каковым являют­ся: дроссель, диафрагмы, сопла, штуцера, вентиль, кран, сужение трубы и т.д.), сопровождаю­щееся изменением температуры, вызванным затратой энергии на преодоление внутренних молекулярных сил взаимного притяжения. Процесс, происходящий при этих условиях, т.е. при постоянстве энтальпии, называется адиабатическим. Изме­нение температуры газа при изоэнтальпийном его расширении называется дроссель-эффектом и установлено Джоулем и Томсоном. Отношение изменения температуры к изменению давления называется коэффициентом Джоуля-Томсона.

Коэффициент Джоуля-Томсона зависит от состава газа, давления и температуры, изменяется в широких пределах и, может иметь положительный и отрицательный знак. Отрицательный знак коэффициента Джоуля-Томсона показывает, что дроссели­рование сопровождается нагреванием газа. Для природных газов при температурах и давлениях, встречаемых на практике, дросселирование практически всегда сопровождается ох­лаждением газа. На Астраханском газоконденсатном месторождении при давлениях, близких к начальному коэффициент Джоуля-Томсона отрицательный. С увеличением давления за его критическим значением коэффициент Джоуля-Томсона уменьшается и проходит через нуль, т.е. через инверсионную точку, и становится отрицательным. В этом случае газ при дросселировании нагревается. Чем выше давление, тем значительнее нагревание газа.

Значение коэффициента Джоуля-Томсона может быть определено эксперимен­тально и расчетным путем. Для проведения термогазогидродинамических расчетов используют аналитический способ определения коэффициента Джоуля-Томсона D_i по формуле:

(2.76)

В формуле (2.76) Т_кр, Р_кр – критические температура и давление газа, метод определения которых в зависимости от состава газа изложен ранее; f(D_i) – функция, определяемая по графику из рисунка 2.30 в зависимости от приведенных давления и температуры газа. Функция f(D_i) имеет размерность теплоемкости газа.

Графические зависимости f(D_i), показанные на рисунке 2.30 в диапазоне изменений 1,6≤T_пp≤2,1 и 0,8≤Р_пр≤3,5, могут быть выражены формулой:

(2.77)

Или (одно и тоже) Обобщенная функция Джоуля-Томсона равна

кДж/кг*К

Для определения изменения температуры в результате дросселирования газа можно пользоваться номограммой, построенной для метана и показанной на рисунке 2.31. Для определения величины температуры газа после дросселирования на графике находят точку с координатами, соответствующими давлению Р₁ и температуре Т₁ до дрос­селирования. От этой точки проводят параллельно ближайшей изоэнтальпийной кри­вой линию до заданного после дросселирования давления Р₂ и определяют Т₂.

Средний коэффициент Джоуля-Томсона при использовании изоэнтальпийных диаф­рагм определяется по формуле:

D_i=ΔТ/ΔР (2.78)

Рисунок 2.30 – Зависимость обобщенной функции f(D_i) от приведенных давления и температуры.

Рисунок 2.31 – Номограмма для определения интегрального дроссель-эффекта метана.

или из выражения для определения конечной температуры газа после дросселирования:

(2.79)

где

=(Р₁+Р₂)/2Р_п.кр; Т_пр1=Т₁/Т_п.кр; = (P_пр, Т_пр1); (2.80)

– средний коэффициент теплоемкости, рассчитанный для условий средних до и после дросселя давлений и температуры.

Интегральный дроссель-эффект может быть рассчитан и по уравнению состояния Битти-Бриджмена согласно [18].

Гидратообразование газов (РИС 97-107)