Поверхности. Классификация. Определитель. Задание на чертеже. Очерк. Каркас.
Линейчатые поверхности. Торсы. Цилиндрические и конические поверхности. Многогранники. Линейчатые поверхности с плоскостью параллелизма.
Поверхности вращения. Конус. Цилиндр. Сфера. Тор. Эллипсоид. Параболоид. Гиперболоид.
Винтовые поверхности. Прямой и наклонный геликоид.
1. Поверхности. Классификация. Определитель. Задание на чертеже. Очерк. Каркас.
Поверхность – это непрерывная совокупность последовательных положений переменной образующей (линии), перемещающейся по определенному закону.
Поверхности могут быть заданы аналитически, то есть уравнениями и называться алгебраическими или трансцендентными, и графически - на чертеже.
Уравнение поверхности Ф (х,у,z) =0 n-ой степени, значит поверхность называется алгебраической n – го порядка. Поверхность первого порядка суть плоскость.

 Классификация поверхностей
Классификация поверхностей



 Линейчатые поверхности Нелинейчатые поверхности
Линейчатые поверхности Нелинейчатые поверхности





 Развертывающиеся Неразвертывающиеся С постоянной образ С перемен. образ.
Развертывающиеся Неразвертывающиеся С постоянной образ С перемен. образ.



 Гранные: С плоскостью параллелизма: Вращения: Циклические:
Гранные: С плоскостью параллелизма: Вращения: Циклические:
Пирамидальные Цилиндроид Сфера Поверхность
Призматические Коноид Тор труб перемен-
Косая плоскость Параболоид ного сечения
 Торсовые: ВинтовыеЦиклическиеКаркасные:
Торсовые: ВинтовыеЦиклическиеКаркасные:
Конические (с направляющим конусом): (трубчатые) Поверхность
Цилиндрические Геликоид: прямой, поверхность земли, обуви,
Торсовые наклонный, развертывающ. изогнутых фюзеляжа
труб самолета
ЛЕКЦИЯ 5-2
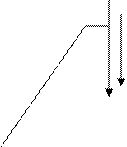
Совокупность независимых факторов (условий), задающих поверхность, называются определителем поверхности. Зададим некоторую поверхность Ф и спроецируем ее на плоскость проекций П.



 Линия видимого контура
Линия видимого контура

 Ф
Ф

 Проецирующие лучи
Проецирующие лучи
 |  | ||||||||
 |  |  | |||||||


 Очертание поверхности
Очертание поверхности
П

Рис. 1
Очерк поверхности (очертание) – проекция видимого контура или граница, которая отделяет проекцию поверхности от остальной плоскости проекций. Дает линию видимости на плоскости проекций, т.е. отделяет видимую часть поверхности от невидимой.
Каркас поверхности – множество точек, линий, принадлежащих поверхности и подчиняющихся определенному закону (закону каркаса). Каркас может быть точечным или линейным.
Критерий задания поверхности: поверхность считается заданной, если относительно любой точки пространства можно решить вопрос принадлежит ли заданная точка поверхности или не принадлежит.
2. Линейчатые поверхности.
Линейчатой поверхностью называется поверхность,образованная произвольно движущейся в пространстве прямой- образующей. Неподвижные линии, пересекающие все образующие поверхности, называются направляющими. В зависимости от вида направляющихся линий и характера движения образующей получаются различные типы
линейчатых поверхностей.
ЛЕКЦИЯ 5-3
Торс или поверхность с ребром возврата – называется поверхность, образованная непрерывным движением прямолинейной образующей l, касающейся во всех своих положениях некоторой пространственной кривой m, называемой ребром возврата.Ребро возврата – направляющая, ее задания достаточно для задания самой поверхности.
1. 




 Если направляющей торса является плоская линия, то поверхность касательных превращается в плоскость (рис.2). Касательные образующие покрывают ее неравномерно и не целиком.
Если направляющей торса является плоская линия, то поверхность касательных превращается в плоскость (рис.2). Касательные образующие покрывают ее неравномерно и не целиком.
 |
 m
m
Рис. 2
-



 Если ребром возврата окажется пространственная кривая m, то точка касания разбивает образующую на положительные и отрицательные полукасательные, которые образуют две полости, граничащие друг с другом по линии m, не перекрывающие одна другую (рис. 3).
Если ребром возврата окажется пространственная кривая m, то точка касания разбивает образующую на положительные и отрицательные полукасательные, которые образуют две полости, граничащие друг с другом по линии m, не перекрывающие одна другую (рис. 3).





 m"
m"



































 |
 m'
m'
Рис.3
- В случае вырождения ребра возврата m в конечную точку S, поверхность торса преобразуется в поверхность коническую (Рис.4). Коническая поверхность образуется прямой линией (образующей), перемещающейся вдоль кривой линии m (направляющей) и имеющей неподвижную точку S (вершину).
Лекция 5 - 4
- В случае вырождения ребра возврата в бесконечно удаленную точку (несобственную), поверхность торса преобразуется в поверхность цилиндрическую (Рис. 5). Рассматривать ее можно как частный случай конической поверхности.



Рис.4 Рис.5
5. Если направляющей поверхности служит ломаная линия, состоящая из отрезков, то цилиндрическая поверхность преобразуется в призматическую, а коническая – в многогранный угол (или в случае замкнутой линии – в пирамиду). Точки на этих поверхностях строятся при помощи проходящих через них образующих.
Конические и цилиндрические поверхности могут быть:
1. Прямыми и наклонными; 2. Если направляющая будет кривой второго порядка, то есть окружность, эллипс, гипербола или парабола, то образуется коническая или цилиндрическая поверхность второго порядка.
Лекция 5 -5
Линейчатые поверхности трех типов: конические, цилиндрические и торсы – относятся к классу развертывающихся линейчатых поверхностей.
Линейчатые поверхности с плоскостью параллелизма.
К этому типу поверхностей относятся такие, все образующие которых параллельны некоторой плоскости, называемой плоскостью параллелизма. В общем случае для определения линейчатой поверхности достаточно задать три направляющие по которым единственным образом будет двигаться образующая. Поэтому задание плоскости параллелизма заменяет одну из необходимых трех направляющих.
Рассмотрим отдельные виды поверхностей:
1. Цилиндроидом называется линейчатая поверхность, имеющая плоскость параллелизма и две криволинейные направляющие. На чертеже (Рис. 7) построены
проекции цилиндроида с плоскостью параллелизма П1 и направляющими АВ и СD. Фронтальные проекции образующих параллельны оси, т. к. являются горизонталями, а горизонтальные проекции строятся по линиям проекционной связи, исходя из того, что образующая пересекает направляющие в любом своем положении.
В" С" В" D"




























 L"
L"



 K"
K" 




 А" D"
А" D"




 А" С"
А" С"



 K' D'
K' D'




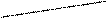

 A' A' C'
A' A' C'
 | |||
 |

 B' C' L'
B' C' L'
 B ' D'
B ' D'
Рис. 7 Рис. 8
2. Коноидом называется линейчатая поверхность, имеющая плоскость параллелизма, одну криволинейную и вторую прямолинейную направляющие. На чертеже (рис. 8) показано построение коноида, имеющего плоскость параллелизма П2 и в качестве направляющих прямую АВ и кривую СD. Точка L принадлежит поверхности.
Коноид называется прямым, если направляющая прямая перпендикулярна к плоскости параллелизма (рис. 9). На рисунке 10 показано построение коноида на эпюре.
Лекция 5 –6
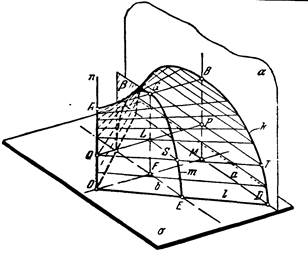

Рис. 9 Рис. 10
3. Гиперболический параболоид или косые плоскости – образуются в результате перемещения прямолинейной образующей по двум направляющим – скрещивающимся прямым линиям, параллельно некоторой плоскости параллелизма.
Если плоскость α перпендикулярна плоскости σ, то параболоид называется прямым (рис. 11). На рисунке 12 показано построение наклонного линейчатого параболоида, где направляющие прямые a и b плоскость параллелизма П1.
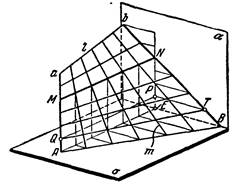

Рис. 11 Рис.12
Лекция 5 –7
ЛЕКЦИЯ 5 (2 часть)
ТЕМА:






