У багатьох випадках необхідно досліджувати не тільки детерміновані, але і випадкові, ймовірнісні (стохастичні) процеси. Зазвичай технологічні процеси виконуються в умовах безперервної зміни обстановки: вимушені простої машин; нерівномірна робота транспорту; безперервна зміна зовнішніх (наприклад, метеорологічних) факторів і т. д. Ті або інші події можуть відбутися а можуть і не відбутися. У зв'язку з цим доводиться аналізувати випадкові, ймовірнісні або стохастичні зв'язки, в яких кожному аргументу відповідає безліч значень функції. Спостереження показали, що, не зважаючи на випадковий характер зв'язку, розсіювання має цілком певні закономірності. Для таких статистичних законів теорія ймовірності дає можливість представити результат не однієї якої-небудь події, а середній результат випадкових подій і тим точніше, чим більше кількість явищ, що аналізуються. Це пов'язано з тим, що, не зважаючи на випадковий характер подій, вони підкоряються певним закономірностям, що розглядаються в теорії ймовірності.
Теорія ймовірності вивчає випадкові події і базується на наступних основних показниках. Сукупність множини однорідних подій випадкової величини х складає первинний статистичний матеріал. Сукупність, що містить всі можливі варіанти масового явища, називають генеральною сукупністю або великою вибіркою N. Зазвичай вивчають лише частину генеральної сукупності, яку називають вибірковою сукупністю або малою вибіркою  . Ймовірністю р(х) події х називають відношення числа випадків N(x), які приводять до настання події х, до загального числа можливих випадків N:
. Ймовірністю р(х) події х називають відношення числа випадків N(x), які приводять до настання події х, до загального числа можливих випадків N:
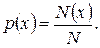
Теорія ймовірності розглядає теоретичні розподіли випадкових величин і їх характеристики. Математична статистика займається способами обробки і аналізу емпіричних подій. Ці дві споріднені науки складають єдину математичну теорію масових випадкових процесів, широко вживану в наукових дослідженнях.
При дослідженні ймовірнісних систем широкого поширення набули дисперсійний, регресійний, кореляційний і спектральний аналізи, а також їх різні комбінації (наприклад, кореляційно-спектральний аналіз).
У дослідженнях часто виникає необхідність виявлення факторів або їх комбінацій, що істотно впливають на процес, що досліджується, оскільки при вимірюванні якої-небудь величини результати зазвичай залежать від багатьох факторів. Практика показує, що основними факторами, як правило, є технічний стан приладу і увага оператора. Для встановлення основних факторів і їх впливу на процес, що досліджується, використовується дисперсійний одно- і багатофакторний аналіз. Суть однофакторного дисперсійного аналізу розглянемо на прикладі. Нехай необхідно перевірити степінь точності групи 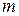 приладів і встановити, чи є їх систематичні похибки однаковими, тобто вивчити вплив одного фактора-приладу на похибку вимірювання. Кожним приладом виконано
приладів і встановити, чи є їх систематичні похибки однаковими, тобто вивчити вплив одного фактора-приладу на похибку вимірювання. Кожним приладом виконано  вимірювань одного і того ж об'єкту, а всього
вимірювань одного і того ж об'єкту, а всього  вимірювань. Окреме вимірювання
вимірювань. Окреме вимірювання  , де
, де  - номер приладу, що має значення від 1 до
- номер приладу, що має значення від 1 до 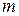 ;
;  - номер виконаного на цьому приладі вимірювання, що змінюється від 1 до
- номер виконаного на цьому приладі вимірювання, що змінюється від 1 до  . Дисперсійний аналіз допускає, що відхилення підпорядковані нормальному закону розподілу, відповідно до якого обчислюють для кожної серії вимірювань середньоарифметичне значення і середню з показань першого приладу і так далі для кожного з
. Дисперсійний аналіз допускає, що відхилення підпорядковані нормальному закону розподілу, відповідно до якого обчислюють для кожної серії вимірювань середньоарифметичне значення і середню з показань першого приладу і так далі для кожного з  вимірювань і
вимірювань і  приладів. В результаті розрахунків встановлюють величину
приладів. В результаті розрахунків встановлюють величину 
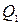

Яку називають сумою квадратів відхилень між вимірюваннями серій. Вона показує степінь розбіжності в систематичних похибках усіх 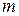 приладів, тобто характеризує розсіювання досліджуваного чинника між приладами.
приладів, тобто характеризує розсіювання досліджуваного чинника між приладами.
Тут  ─ середньоарифметичне для
─ середньоарифметичне для  вимірювань;
вимірювань;  ─ середньоарифметичне для всіх серій вимірювань, тобто загальне середнє значення.
─ середньоарифметичне для всіх серій вимірювань, тобто загальне середнє значення.
Визначається також величина  за формулою
за формулою

де  ─ окреме
─ окреме  -e вимірювання на
-e вимірювання на  -му приладі.
-му приладі.
Величину  називають сумою квадратів відхилень всередині серії. Вона характеризує залишкове розсіювання випадкових похибок одного приладу.
називають сумою квадратів відхилень всередині серії. Вона характеризує залишкове розсіювання випадкових похибок одного приладу.
При такому аналізі допускається, що центри нормальних розподілів випадкових величин рівні (або рівні з певним степенем точності), у зв'язку з чим всі  вимірювання можна розглядати як вибірку з однієї і тієї ж нормальної сукупності. Щоб переконатися в можливості такого припущення, обчислюють критерій
вимірювання можна розглядати як вибірку з однієї і тієї ж нормальної сукупності. Щоб переконатися в можливості такого припущення, обчислюють критерій

чисельник і знаменник якого є дисперсіями  для
для 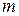 і
і  спостережень відповідно. Залежно від значень
спостережень відповідно. Залежно від значень  і
і  числа степенів вільності і ймовірності р (наприклад, 0,95; 0,99 і ін.) складені табличні значення
числа степенів вільності і ймовірності р (наприклад, 0,95; 0,99 і ін.) складені табличні значення 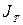 . Якщо
. Якщо  , то вважається, що в даному прикладі всі прилади мають однакові (допустимі) систематичні помилки.
, то вважається, що в даному прикладі всі прилади мають однакові (допустимі) систематичні помилки.
Дисперсійний аналіз є багатофакторним, якщо він має два чинники і більше. Суть його принципово не відрізняється від однофакторного, але істотно збільшується кількість розрахунків.
Методи теорії ймовірності і математичної статистики часто застосовуються в теорії надійності, яка широко застосовується в різних галузях науки і техніки. Під надійністю розуміють властивість виробу (об'єкту) виконувати задані функції (зберігати встановлені експлуатаційні показники) протягом необхідного періоду часу. Забезпечення надійності (виключення відмов, порушень працездатності) продукції стало одним з основних народногосподарських завдань. У теорії надійності відмови розглядають як випадкові події. Для кількісного опису відмов застосовуються математичні моделі - функції розподілу ймовірності інтервалів часу. Найчастіше застосовуються закони нормального і експоненційного розподілу, закон Вейбулла і деякі інші.
Основним завданням теорії надійності є прогнозування (прогноз з тією або іншою ймовірністю) різних показників безвідмовної роботи (довговічності, терміну служби і так далі), що пов'язане із знаходженням ймовірності.
Для дослідження складних процесів імовірнісного характеру застосовують метод Монте-Карло, за допомогою якого знаходять якнайкраще рішення з множини даних варіантів. Цей метод статистичного моделювання або статистичних випробувань заснований на використанні випадкових чисел, що моделюють імовірнісні процеси. Результати рішень за цим методом дозволяють встановити емпіричні залежності процесів, що досліджуються. Математичною основою методу є закон великих чисел, розроблений П. Л. Чебишовим, який формулюється так: при великій кількості статистичних випробувань ймовірність того, що середньоарифметичне значення випадкової величини прямує до її математичного сподівання, дорівнює 1, тобто

де  - будь-яке мале додатне число.
- будь-яке мале додатне число.
З цієї формули видно, що при збільшенні кількості випробувань  середньоарифметичне необмежено (асимптотично) наближається до математичного сподівання.
середньоарифметичне необмежено (асимптотично) наближається до математичного сподівання.
Послідовність розв’язання задач методом Монте-Карло зводиться до збору, обробки і аналізу статистичних спостережень процесу, що досліджується: відбору головних, відкиданню другорядних факторів і складанню адекватної математичної моделі (рівнянь, графіків, циклограм і т. д.); складанню алгоритмів і розв’язання задачі на ЕОМ.
Для розв’язування задач методом Монте-Карло необхідно мати статистичний ряд, знати закон його розподілу, середнє значення  і математичне сподівання
і математичне сподівання  , середньоквадратичне відхилення. За допомогою методу можна отримати розв’язок з будь-якою заданою точністю, тобто
, середньоквадратичне відхилення. За допомогою методу можна отримати розв’язок з будь-якою заданою точністю, тобто  . При нормальному законі розподілу точність результатів, отриманих методом Монте-Карло, оцінюється за формулою
. При нормальному законі розподілу точність результатів, отриманих методом Монте-Карло, оцінюється за формулою 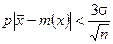 .
.
Нехай, наприклад, за умовою задачі задана допустима помилка  . Якщо при наявній кількості ряду
. Якщо при наявній кількості ряду  і
і  помилка
помилка  виявиться більшою, ніж
виявиться більшою, ніж  , то необхідно збільшити кількість випробувань до
, то необхідно збільшити кількість випробувань до  і обчислити нове значення помилки
і обчислити нове значення помилки 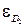 , і т. д., поки не буде виконуватись умова
, і т. д., поки не буде виконуватись умова  (
( - кількість випробувань). Слід при цьому підкреслити, що вирішення завдань методом Монте-Карло ефективне лише з використанням швидкодіючих ЕОМ.
- кількість випробувань). Слід при цьому підкреслити, що вирішення завдань методом Монте-Карло ефективне лише з використанням швидкодіючих ЕОМ.
При дослідженнях процесів і об'єктів часто застосовують методи, засновані на теорії масового обслуговування (ТМО), з метою знаходження умов найбільшої ефективності роботи системи «вимога - обслуговування». Під обслуговуванням розуміють задоволення якої-небудь заявки. Таким чином, в ТМО система складається з кількості (потоку) вимог, обслуговуючого приладу (апарату) і вихідного потоку. Залежно від умов функціонування системи кількість вимог створює черга на обслуговування.
Основними характеристиками ТМО є: інтенсивність надходження вимог або заявок на обслуговування  ; інтенсивність обслуговування (пропускна спроможність приладу обслуговування)
; інтенсивність обслуговування (пропускна спроможність приладу обслуговування)  ; коефіцієнт використання системи
; коефіцієнт використання системи  ; час очікування в черзі до обслуговування
; час очікування в черзі до обслуговування 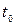 ; тривалість обслуговування
; тривалість обслуговування  ; час обслуговування в системі
; час обслуговування в системі  ; кількість вимог в черзі
; кількість вимог в черзі  ; математичне сподівання кількості вимог в системі
; математичне сподівання кількості вимог в системі  . Ці характеристики мають наступні співвідношення:
. Ці характеристики мають наступні співвідношення: 
Знак «−» означає, що при розрахунку приймаються середні випадкові значень  . Розподіл часу обслуговування за тривалістю найчастіше виражається показниковим законом.
. Розподіл часу обслуговування за тривалістю найчастіше виражається показниковим законом.
У ТМО інтенсивність обслуговування завжди вища за інтенсивність вимоги, тобто  . Проте, не дивлячись на те, що
. Проте, не дивлячись на те, що 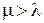 , виникають черги на обслуговування, оскільки
, виникають черги на обслуговування, оскільки  з ряду причин величина змінна, а інтервал між обслуговуванням неритмічний. В результаті завданням ТМО є встановлення найбільш достовірних залежностей між інтенсивністю потоку вимог і продуктивністю (пропускною спроможністю, кількістю і ефективністю обслуговування) системи. Показниками ефективності функціонування системи можуть бути
з ряду причин величина змінна, а інтервал між обслуговуванням неритмічний. В результаті завданням ТМО є встановлення найбільш достовірних залежностей між інтенсивністю потоку вимог і продуктивністю (пропускною спроможністю, кількістю і ефективністю обслуговування) системи. Показниками ефективності функціонування системи можуть бути  , зведена вартість і ін.
, зведена вартість і ін.
Теорія масового обслуговування базується на аналізі випадкових процесів. При вирішенні тих або інших практичних завдань в кожному випадку повинні прийматися індивідуальні рішення.
Для оптимізації різних процесів використовуються методи теорії ігор, яка розглядає розвиток процесів залежно від випадкових ситуацій. Теорію ігор можна назвати математичною теорією конфліктів, пов'язаних з тим, що інтереси двох сторін не співпадають. Прикладом конфліктної ситуації є, наприклад, спортивні ігри. Як правило, теорія ігор розглядає конфліктні ситуації при частковій або повній відсутності даних про обстановку. Тому можуть бути і випадкові ходи, ефект від яких можна оцінити в середньому математичним сподіванням. Методи теорії ігор застосовуються також не тільки при дослідженні дійсно конфліктних ситуацій, але і при вирішенні таких задач, в яких як «супротивник» виступає, наприклад, природа. Такі задачі зазвичай виникають при будівництві різних споруд, в сільському господарстві, метеорології і ін. За допомогою теорії ігор можна оцінювати найбільш сприятливі і несприятливі ситуації і на їх основі приймати оптимальне для даних умов рішення.






