Метод диференціальних рівнянь

Лекція №6. Аналітичні методи

 

Універсального методу складання диференційних рівнянь не існує, можна лише використовувати деякі загальні підходи до складання рівнянь першого порядку.

Геометричні або фізичні задачі зазвичай призводять до одного з наступних трьох видів рівнянь:

1) диференціальні рівняння в диференціалах;

2) диференціальні рівняння в похідних;

3) прості інтегральні рівняння з подальшим перетворенням їх в диференціальні рівняння.

Розглянемо, як складаються рівняння кожного з наведених видів окремо.

1. Рівняння в диференціалах. При складанні диференціальних рівнянь першого порядку зручно застосовувати «метод диференціалів». Суть його полягає в тому, що згідно з умовою завдчі складаються наближені співвідношення між диференціалами. Для цього малі прирости величин замінюються їх диференціалами, нерівномірно протікаючі фізичні процеси протягом малого проміжку часу розглядаються як рівномірні.

Ці припущення і заміни не відбиваються на остаточних результатах унаслідок того, що заміна приростів диференціалами зводиться до відкидання нескінченно малих вищих порядків мализни. Оскільки відношення диференціалів функції і аргументу є границею відношення їх приростів, то в міру того, як прирости прямують до нуля, прийняті припущення виконуються все з більшою точністю. Отримані при цьому диференціальні рівняння, виявляються точними, якщо вони однорідні і лінійні щодо диференціалів.

Розглянемо геометричний приклад застосування методу диференціалів.

Нехай перед дослідником стоїть завдання визначення поверхні обертання, по якій потрібно відшліфувати дзеркало рефлектора, щоб світлові промені, що виходять з однієї точки, після відбиття в дзеркалі перетиналися в іншій точці.

По суті, ця завдача зводиться до знаходження рівняння перетину шуканої поверхні меридіанною площиною, що проходить через точку , в якій розміщується джерело світла, і точку , в якій перетинаються відбиті промені (рис. 6.1).

Нехай MQ - мала дуга цього перетину. Її вважатимемо прямолінійним відрізком. Опишемо з точок і , як з центрів, дуги MN і МР кіл радіусами і 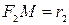. Ці дуги також вважатимемо прямолінійними відрізками.

Трикутники MQN і MQP ─ прямокутні ( MNQ і MPQ - прямі) із загальною гіпотенузою MQ.

Користуючись відомим законом оптики про рівність кутів падіння і від-

 

Рис. 6.1. Розрахункова схема

биття, а також властивістю рівності вертикальних кутів, знаходимо, що MQN = MQP і MQN = MQP. Звідси витікає, що QN=QP. Оскільки ,а 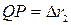, то, замінюючи прирости радіусів-векторів і їх диференціалами, маємо

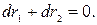
Диференціальне рівняння складене. Воно легко інтегрується. Для цього перепишемо його таким чином:

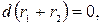
звідки знаходимо загальний інтеграл

Отже, перетин шуканої поверхні меридіанною площиною є еліпсом. Отже, дзеркало рефлектора треба відшліфувати у вигляді поверхні еліпсоїда обертання.

2. Рівняння в похідних. Для складання диференціальних рівнянь використовується видозмінений метод диференціалів, який іменують методом похідних.

Суть методу похідних полягає в тому, що згідно з умовою завдання складаються наближені співвідношення між швидкостями зміни функції і аргументу. При цьому часто використовується геометрична інтерпретація швидкості ─ кутовий коефіцієнт дотичної. Відсутність нескінченна малих в методі похідних позірна, оскільки швидкість зміни досліджуваної величини сама з'явилася на основі розгляду нескінченно малих елементів.

Наприклад, при дослідженні зростання числа публікацій в науці виходять з припущення, що швидкість росту пропорційна досягнутому рівню у числа публікацій. Це тотожно твердженню, що відносна швидкість зростання .

Вказане припущення дозволяє скласти диференціальне рівняння у формі

або

де = const, що характеризує в середньому відгуки на публікації в тій або іншій області знання.

Розв’язок цього диференціального рівняння має вигляд

де а ─ постійна, що характеризує деяке початкове число публікацій.

3. Прості інтегральні рівняння. При розгляді роботи сил, об'ємів тіл, площ криволінійних поверхонь їх можна описати за допомогою певного інтеграла або інтегральних формул. У випадку якщо при такому описі невідомі функції потрапляють під знак інтеграла, то отримуємо формальний запис, який і називається інтегральним рівнянням.

Подальше диференціювання інтегрального рівняння перетворить його в диференціальне.

Для ілюстрації методу побудови інтегральних рівнянь з подальшим перетворенням їх у диференціальні розглянемо наступне завдання.

Нехай потрібно знайти закон прямолінійного руху матеріальної точки маси 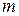, якщо відомо, що робота сили, що діє на точку, пропорційна часу t, що пройшов від початку руху. Початковий шлях і початкова швидкість рівні відповідно і .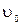

З курсу механіки відомо, що у разі прямолінійного переміщення точки, коли напрями сили і швидкості співпадають, робота , де ─ сила, яка діє на точку. З умови задачі

.

Порівнюючи обидва вирази для А, знаходимо

.

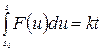Шляхом диференціювання по s отримуємо

,

але оскільки ─ швидкість руху і

,

то

.

З іншого боку, згідно з другим законом Ньютона маємо, що

Порівнюючи обидва вирази для F (s), складаємо диференціальне рівняння

Загальний розв’язок цього рівняння має вигляд

Згідно з початковою умовою при 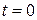знаходимо, що

.

Отже,

Замінюючи на і інтегруючи, знаходимо

При , отже

Таким чином, закон руху матеріальної точки приймає вигляд

При складанні диференціальних рівнянь об'єктів, що регулюються, необхідно перш за все визначити умови отримання рівноважного режиму роботи об'єкту, тобто рівняння статичної рівноваги.

У багатьох випадках рівняння статичної рівноваги виявляється загальним для різних об'єктів дослідження. Наприклад, у разі поступального руху досліджуваний об'єкт знаходитиметься в стані статичної рівноваги (рух буде рівномірним) тільки у тому випадку, коли рушійні сили дорівнюють силам опору . Рівняння статичної рівноваги приймає вигляд

У тому випадку, коли об’єкти дослідження (колінчастий вал двигуна внутрішнього згорання, ротори електродвигунів та генераторів, турбіни тощо) здійснюють обертальний рух, то умовою статичної рівноваги є рівність між обертальним моментом і моментом спротиву обертанню , тобто

.

Для регульованого резервуару, в якому необхідно підтримувати постійний рівень, умовою статичної рівноваги є рівняння

де ─ прихід рідини в резервуар; 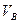─ витрата рідини.

Аналогічно виглядає рівняння статичної рівноваги регулятора ресівера з газом або парою

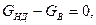
де , 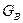─ маси газу, що надходить і виходить з ресівера відповідно.

Якщо регульованим об'єктом є об'єм, в якому повинна підтримуватися постійна температура, то умова статичної рівноваги отримує вигляд

де ─ кількість теплоти, що надходить до об'єму в одиницю часу; ─ кількість теплоти, що виходить з об'єму в одиницю часу.

Перехідний процес в досліджуваному об'єкті може з'явитися тільки в тому випадку, якщо буде порушено статичну рівновагу. Поява приросту одного з членів рівняння cтатичної рівноваги неминуче спричинить прирости і другого члена рівняння, причому такі прирости, як правило, не рівні між собою. В результаті умова статичної рівноваги порушується і тоді при поступальному русі

при обертальному русі

при заповненні резервуару рідиною

при заповненні ресівера газом

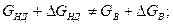
при порушенні теплового режиму

Отримані нерівності можуть бути спрощені, якщо врахувати в них умову статичної рівноваги:

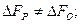
Таким чином, при порушенні умов статичної рівноваги в досліджуваному об'єкті виникає надлишок або недостача рушійних сил (або моментів), надходження рідини, газу, надлишок або недостача теплоти. Цей надлишок або недостача викликає зміну характеру роботи об'єкту.

Подальше перетворення отриманих нерівностей здійснюється шляхом залучення загальновідомих залежностей, принципів, законів або аналізу вихідних характеристик об'єкту, отриманих в пошуковому експерименті. При цьому можуть використовуватися феноменологічні закони (такі, як закони Гука, Фур’є), напівемпіричні співвідношення (наприклад, додаткове співвідношення Ньютона в теорії удару) і чисто емпіричні співвідношення.

Будь-які диференціальні рівняння ─ це модель цілого класу явищ, тобто сукупність явищ, що характеризуються однаковими процесами. При інтегруванні рівнянь отримують велику кількість розв’язків, що задовольняють початковому диференціальному рівнянню. Для того, щоб отримати з множини можливих рішень одне, що задовольняє тільки даному процесу, необхідно задати додаткові умови диференціальному рівнянню. Вони повинні чітко виділити явище, що вивчається, зі всього класу явищ.

Умови, які розкривають всі особливості даного рівняння, називаються умовами однозначності і характеризуються наступними ознаками: геометрією системи (форма і розміри тіла); фізичними властивостями тіла (теплопровідність, вологопровідність, пружність тощо); початковими умовами, тобто станом системи в початковий момент; граничними умовами, тобто умовами взаємодії системи на межах з навколишнім середовищем. Початкові і граничні умови називають краєвими.

Розглянуті приклади вибору виду моделі об'єкту мають відношення лише до таких об'єктів, які можуть розглядатися як детерміновані.

Розглянемо способи вибору виду математичних моделей для ймовірнісних об'єктів.

Як і раніше, для статичних об'єктів під стаціонарністю входу розумітимемо постійне його значення. Якщо вхідний сигнал приймає декілька значень, то його вважатимемо нестаціонарним.

Нехай є одновимірно-одновимірна схема взаємодії об'єкту із зовнішнім середовищем. Якщо дія на вході об'єкту постійна у часі, то як математична модель статичного ймовірнісного об'єкту може виступати деякий закон розподілу вихідної величини. Якщо вхідна дія може приймати різні значення і кожному значенню відповідає ряд значень вихідної величини об'єкту, то як модель ймовірнісного об'єкту приймається набір законів розподілу вихідної величини для всіх значень вхідної дії.

При моделюванні ймовірнісних об'єктів крім законів розподілу вхідних і вихідних величин істотним є також зв'язок між ними. Тому до складу моделі включають коефіцієнти взаємної кореляції і функції

де х - вхідна дія; ─ максимальна ентропія вихідних характеристик; R ─ відносна організація вихідних характеристик; ─ середнє значення вихідної величини; 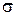─ середньоквадратичне відхилення вихідних величин.

Максимальна ентропія вихідних характеристик оцінюється за формулою

де ─ кількість станів об'єкту.

Для оцінки кількості станів об'єкту використовується формула

де ─максимальне і мінімальне значення вихідної величини; 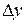─ точність вимірювання вихідних величин.

Відносна організація вихідних характеристик оцінюється за формулою Ферстера

де

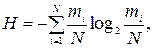
тут ─ кількість появ значення 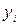вихідної характеристики; N ─ повна кількість спостережень вихідних характеристик.

При багатовимірно-одновимірній схемі взаємодії статичного ймовірнісного об'єкту із зовнішнім середовищем завдання математичного моделювання зводиться до одновимірно-одновимірної схеми для кожного поєднання постійних вхідних дій.

Нестаціонарний випадок відрізняється тим, що кожна вхідна дія може приймати декілька значень. При цьому для кожного конкретного сполучення задача аналізу зв'язку між входами і виходом може вирішуватися аналогічно задачі для багатовимірно-одновимірної стаціонарної схеми.

Оцінка степені зв'язку виходу з входами проводиться шляхом зіставлення статичних параметрів і обчислення коефіцієнтів взаємної кореляції.

Моделювання об'єкту при одновимірно-багатовимірній і багатовимірно-багатовимірній схемах взаємодії проводиться аналогічно вищевикладеному.

Процес вибору математичної моделі об'єкту закінчується її попереднім контролем. При цьому здійснюються наступні види контролю: розмірностей; порядків; характеру залежностей; екстремальних ситуацій; граничних умов; математичної замкнутості; фізичного змісту; стійкості моделі.

Контроль розмірностей зводиться до перевірки виконання правила, згідно якому прирівнюватися і складатися можуть тільки величини однакової розмірності.

Контроль порядків направлений на спрощення моделі. При цьому визначаються порядки величин, що додаються, і явно малозначні доданки відкидаються.

Контроль характеру залежностей зводиться до перевірки напряму і швидкості зміни одних величин при зміні інших. Напрями і швидкість, згідно з математичною моделлю, повинні відповідати фізичному змісту задачі.

Контроль екстремальних ситуацій зводиться до перевірки наочного змісту розв’язку при наближенні параметрів моделі до нуля або нескінченності.

Контроль граничних умов полягає в тому, що перевіряється відповідність математичної моделі граничним умовам, що витікають зі змісту задачі. При цьому перевіряється, чи дійсно граничні умови поставлені і враховані при побудові шуканої функції і чи дійсно функція задовольняє таким умовам.

Контроль математичної замкнутості зводиться до перевірки того, що математична модель дає однозначний розв’язок.

Контроль фізичного змісту зводиться до перевірки фізичного змісту проміжних співвідношень, що використовуються при побудові математичної моделі.

Контроль стійкості моделі полягає в перевірці того, чи варіювання вихідних даних в рамках наявних даних про реальний об'єкт не приведе до істотної зміни розв’язку.

 

Аналітичні методи

 

Другим етапом вирішення практичних завдань математичними методами є вибір методу дослідження моделі. Вибір методу дослідження математичної моделі безпосередньо пов'язаний з такими поняттями, як зовнішня і внутрішня правдоподібність дослідження.

Під зовнішньою правдоподібністю дослідження розуміється очікуваний ступінь адекватності математичної моделі реальному об'єкту за властивостями, що цікавлять дослідника.

Під внутрішньою правдподібністю дослідження розуміється очікуваний степінь точності розв’язку отриманих рівнянь, які прийняті за математичну модель об'єкту.

Якщо вид моделі вже вибраний, то зовнішня правдоподібність моделі вважається фіксованою і вибір методу дослідження буде цілком визначатися необхідним степенем внутрішньої правдоподібності.

У переважній більшості випадків при виборі методу дослідження керуються принципом відповідності зовнішньої і внутрішньої правдоподібності, аналогічним відомому правилу наближених обчислень: степінь точності обчислень повиненна відповідати степені точності вихідних даних. Проте, залежно від умов і завдань дослідження можливі відхилення від такого принципу. Перерахуємо деякі з них:

1) якщо мова йде про розробку нового єдиного методу досліджень, який передбачається застосовувати для широкого, заздалегідь не фіксованого, класу моделей, то потрібно прагнути до максимальної внутрішньої правдподібності дослідження незалежно від рівня зовнішньої правдоподібності;

2) якщо здійснюється перевірка зовнішньої правдоподібності моделі, то внутрішня правдоподібність вибраного методу перевірки повинна бути максимальною;

3) якщо модель настільки проста, що для неї легко отримати точне розв’язок, то штучно знижувати строгість розв’язку безглуздо.

У інших випадках перевага віддається «принципу рівної правдоподібності».

Вибір методу дослідження тим ефективніший, чим більше є відомостей про кінцеве рішення задачі. Такі відомості можуть бути отримані шляхом попередніх прикидочних досліджень моделі або її елементів.

В процесі прикидочних досліджень здійснюється порівняння величин окремих членів рівнянь в діапазоні, що вивчається, зміни змінних і параметрів задачі. Відносно малі доданки відкидаються, нелінійні залежності замінюються на лінійні. Деякі з компонентів моделі апроксимуються грубими рівняннями. Все це дозволяє швидко отримати приблизний розв’язок задачі.

Будь-які знання, хоча б і приблизні, якісних і кількісних характеристик шуканого розв’язку допомагають при виборі точності методу дослідження. Іноді навіть приблизний розв’язок виявляється достатнім. Як приклад можна навести задачу про пошук експериментального значення функції. Якщо точка екстремуму є стаціонарною, то навіть груба похибка в її знаходженні мало позначиться на підрахунку цього значення. Тому застосування високоточних методів пошуку такого екстремуму нераціонально. Громіздкі точні обчислення в цьому випадку створюють лише ілюзію точності. У разі застосування грубої математичної моделі не слід застосовувати громіздкі обчислювальні методи.

Вибір методу дослідження математичної моделі багато в чому зумовлений її виглядом.

Статичні системи, представлені за допомогою рівнянь алгебри, досліджуються за допомогою визначників, методу ітерацій, методів Крамера і Гауса. У разі ускладнень з аналітичними розв’язками використовуються наближені методи: графічний метод; метод хорд; метод дотичних; метод ітерацій. В останньому випадку, який вимагає контролю точності (числа значущих цифр) залежно від грубості обчислювального методу, доцільне застосування ЕОМ.

Дослідження динамічних режимів функціонування об'єкту, представлених в класі диференціальних рівнянь, також зумовлюється класом, до якого відноситься рівняння, що розв’язується.

Якщо в результаті розв’язування рівнянь алгебри отримуємо числа, то при розв’язуванні диференціальних рівнянь отримуємо функції.

Для розв’язування диференціальних рівнянь широко використовуються метод розділення змінних, метод підстановки, метод інтегруючого множника, метод якісного аналізу і тому подібне Для отримання наближених розв’язків використовують метод послідовних наближень, метод функціональних рядів, метод Рунге-Кутта, чисельні методи інтеграції і тому подібне.

Для докладного вивчення моделей динамічних систем, побудованих в класі диференціальних рівнянь, використовується якісна теорія диференціальних рівнянь.

Якісна теорія диференціальних рівнянь дозволяє вивчити всі можливі розв’язки ─ регулярні і особливі.

У основі якісної теорії лежить поняття фазового портрета системи. Побудова фазового портрета проілюструємо наступним прикладом. Нехай розглядається система, що описується наступним диференціальним рівнянням:

з початковими умовами

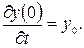
Частинний розв’язок цього рівняння має вигляд

Приймаючи за нову шукану функцію і вводячи позначення

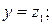
перетворюємо початкове диференціальне рівняння в систему рівнянь першого порядку:

з початковими умовами

Частинний розв’язок запишеться так:

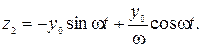
Із отриманої системи рівнянь для і , виключаючи 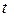, маємо

де

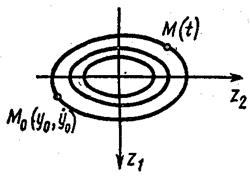
Рис. 6.2. Фазовий портрет системи

 

Останнє рівняння описує еліпс на площині . Отже, частинний розв’язок для і виражається залежністю від часу поточних координат точки M (t), яка починає свій рух у момент 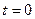від точки і рухається по еліпсу (рис. 6.2). Точка M(t) називається зображувальною точкою. Траекторія такої точки називається фазовою траекторією.

Змінюючи початкові умови, можна отримати сімейство фазових траєкторій, яке називається фазовим портретом, а площина , на якій розташоване це сімейство, ─ фазовою площиною.

При теоретичних дослідженнях широко використовується теорія функцій комплексної змінної. У основі цієї теорії лежить положення про комфорне перетворення, згідно з яким дві криві і 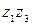з області z, що перетинаються, завжди можна перенести в область відповідно кривим і 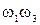, зберігаючи рівність кутів між кривими і в кожній парі. Це дозволяє змінити координати так, щоб спростити громіздкі математичні перетворення.

Розглянуті аналітичні методи, як правило, дозволяють успішно вирішувати лише відносно прості завдання. В той же час все частіше виникає необхідність використання складних диференціальних рівнянь або їх систем з складними початковими і граничними умовами (часто нелінійними). Їх розв’язок досить складний або невідомий, у цих випадках удаються до тих або інших наближених обчислень за допомогою чисельних методів.

Ідея чисельних методів (методи скінченних різниць або сіток) полягає в наступному:

1. У плоскій області G, в якій потрібно знайти розв’язок, будується сіткова область , що складається з однакових клітинок (рис. 6.3) і наближається до області.

2. Задане диференціальне рівняння замінюється у вузлах побудованої сітки відповідним скінченнорізницевим рівнянням.

3. На підставі граничних умов встановлюються значення шуканого рішення в граничних вузлах області .

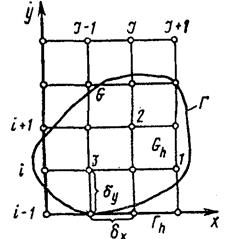
Рис. 6.3. Сіточна область з контуром Г для плоскої області , в якій проводиться розв’язування двовимірного диференціального рівняння

 

Розв’язавши отриману систему скінченнорізницевих рівнянь (для чого необхідно розв’язати алгебричну систему з великою кількістю невідомих), знайдемо значення шуканої функції у вузлах сітки, тобто матимемо чисельний розв’язок поставленої задачі. Вибір сіткової області проводиться залежно від конкретного завдання, але у всіх випадках контур сіткової області , слід вибирати так, щоб він якнайкраще апроксимував контур заданої області G. Сіткова область може складатися з квадратних, прямокутних, трикутних і інших клітинок.

Використання аналітичних методів для розв’язування математичних задач є основним методом сучасного наукового дослідження. Проте громіздкість моделей і прямих методів розв’язування рівнянь ускладнює отримання кінцевих розв’язків. Тому у розв’язанні практичних завдань (особливо управлінських) знайшли широке застосування методи перетворення початкових рівнянь (логарифмування, перетворень Лапласа, Фур’є та інш.).

Логарифмування рівнянь є найпростішим способом перетворення.

Нехай нам необхідно отримати розв’язок простого рівняння

яке називається оригіналом функції.

Піднесення числа а до степені 0,2 прямими методами складно. Тому здійснюється перетворення даного рівняння за допомогою логарифмування

─ це рівняння називається зображенням функції.

При логарифмуванні функція переводиться із простору оригіналів в простір зображень і операція піднесення до степеня зводиться до множення чисел 0,2 і 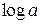, що не викликає ніяких ускладнень.

За допомогою антилогарифмування отриманий результат переводиться з простору зображень в простір оригіналів.

Наведений приклад добре ілюструє і є аналогом перетворень Лапласа і перетворень Фур’є.

Сенс вказаних перетворень аналогічний логарифмуванню. Наприклад, в перетвореннях Лапласа початкова функція часу переводиться з простору оригіналів в простір зображень за допомогою інтеграла

де р ─ оператор Лапласа ().

Перехід функції з простору зображень в простір оригіналів здійснюється за допомогою інтеграла

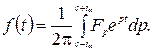
Величина с вибирається так, щоб забезпечити збіжність інтеграла.

Перетворення Лапласа широко використовується при розв’язуванні диференціальних і інтегральних рівнянь. В процесі розв’язування цих рівнянь широко використовуются таблиці перетворень функції, так само як це робиться у разі логарифмування.

На основі методу перетворення функцій розв’язуються задачі аналізу перехідних процесів в системах управління. В процесі аналізу оперують функціями передачі.

Під функцією передачі розуміється відношення перетворення Лапласа вихідного сигнала (реакції) лінійної системи до перетворення вхідного сигнала (впливу) за нульових початкових умов:

де W(p) ─ функція передачі; х(р) ─ перетворення Лапласа вхідного сигналу; у(р) ─ перетворення Лапласа вихідного сигналу.

Вид функції передачі може бути отриманий з диференціального рівняння системи управління шляхом заміни операції диференціювання у часі оператором Лапласа р, а операції інтегрування у часом ─ заміною .

Наприклад, якщо система управління описується диференціальним рівнянням

то, провівши заміну на р і переходячи до зображень, отримуємо

.

Таке представлення диференціального рівняння називається операційним.

Для знаходження функції передачі цієї системи досить провести нескладні алгебричні перетворення. В результаті отримаємо

Окрім методу функцій передачі для аналізу систем управління широко використовується метод частотних характеристик, який складає теоретичну базу узагальненого гармонійного аналізу.

Під частотною характеристикою системи розуміють відношення комплексних зображень за Фур’є вихідного і вхідного сигналів в усталеному режимі гармонійних коливань

де ─ перетворення Фур’є вхідного сигналу; ─ кругова частота; ─ перетворення Фур’є вихідного сигнала.

Аналітично можна отримати з функції передачі заміною параметра перетворення Лапласа р на .

Частотні характеристики систем управління використовують при аналізі стійкості, якості перехідних процесів і динамічної точності, синтезу корегуючи пристроїв.

Окрім перерахованих при вирішенні управлінських завдань широко використовуються: метод простору станів; метод компараментального аналізу; інформаційні методи.