В лабораторной работе № 1 вы решали системы линейных уравнений методом Гаусса. Однако этот метод имеет ряд недостатков: нельзя узнать, совместна система или нет, пока не будут проведены все преобразования, необходимые в методе Гаусса; метод Гаусса непригоден для систем с буквенными коэффициентами.
Рассмотрим другие методы решения систем линейных уравнений. Эти методы используют понятие ранга матрицы и сводят решение любой совместной системы к решению системы, к которой применимо правило Крамера.
Обоснование рассматриваемых методов можно найти, например, в книге А.Г. Куроша «Курс высшей алгебры». Мы опишем их в ходе решения примера.
Пример 1. Найти общее решение следующей системы линейных уравнений с помощью фундаментальной системы решений приведенной однородной системы и частного решения неоднородной системы.
(1)
1. Составляем матрицу A и расширенную матрицу 
системы (1)
; 
.
2. Исследуем систему (1) на совместность. Для этого надо найти ранги матриц A и 
(обозначим их через 
и 
). Если окажется, что 
, то система (1) несовместна. Если же получим, что 
, то эта система совместна и мы ее будем решать. (Исследование на совместность основано на теореме Кронекера-Капелли).
a) Находим .
Чтобы найти , будем рассматривать последовательно отличные от нуля миноры первого, второго и т. д. порядков матрицы A и окаймляющие их миноры.
М1=1≠0 (1 берем из левого верхнего угла матрицы А). Окаймляем М1 второй строкой и вторым столбцом этой матрицы. 
. Продолжаем окаймлять М1 – второй строкой и третьим столбцом. Получим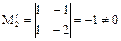 
. Значит, 
. Теперь окаймляем отличный от нуля минор 
второго порядка.
Имеем: 
(так как два первых столбца одинаковы) 
Мы видим, что 
, а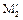 
- базисный минор матрицы A.
b) Находим .
Достаточно базисный минор 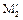матрицы A окаймить столбцом свободных членов и всеми строками (у нас только последней строкой).
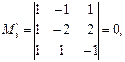этот минор равен 0, так как второй и третий столбцы определителя пропорциональны.
Отсюда следует, что 
и 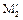остается базисным минором матрицы .
c) Так как , то система (1) совместна. Поскольку =2<4, то система (1) имеет бесконечное множество решений.
Переходим к нахождению общего решения этой системы.
3. Составим приведенную однородную систему (2) для системы (1), заменив в (1) все свободные члены нулями. Затем найдем фундаментальную систему решений (ФСР) системы (2), а через нее и общее решение этой системы.
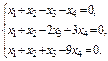(2)
Так как 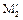- базисный минор матрицы A системы (2), то эта система эквивалентна системе (3), состоящей из первых двух уравнений системы (2) (ибо 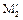находится в первых двух строках матрицы A).
(3)
Так как базисный минор 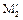находится в первом и третьем столбцах матрицы A, то основными неизвестными в (3) будут x1 и x3. Свободные неизвестные x2 и x4 перенесем в правые части уравнений (3).
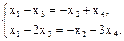(4)
В этой системе два свободных неизвестных (x2 и x4). Поэтому ФСР системы (4) состоит из двух решений. Чтобы их найти, придадим свободным неизвестным в (4) сначала значения x2=1, x4=0, а затем – x2=0, x4=1.
При x2=1, x4=0 получим:
Эта система уже имеет единственное решение (его можно найти по правилу Крамера или любым другим способом). Вычитая из второго уравнения первое, получим:
Ее решением будет x1= -1, x3=0. Учитывая значения x2 и x4, которые мы придали, получаем первое решение системы (2): 
.
Теперь полагаем в (4) x2=0, x4=1. Получим:
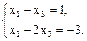
Решаем эту систему по теореме Крамера:
.
Получаем второе решение системы (2): 
.
Решения β1, β2 и составляют ФСР системы (2). Тогда ее общим решением будет 
Здесь с1, с2 – произвольные постоянные.
4. Найдем одно частное решение неоднородной системы (1). Как и в пункте 3, вместо системы (1) рассмотрим эквивалентную ей систему (5), состоящую из первых двух уравнений системы (1):
(5)
Перенесем в правые части свободные неизвестные x2 и x4:
(6)
Придадим свободным неизвестным x2 и x4 произвольные значения, например, x2=2, x4=1, и подставим их в (6). Получим систему
Эта система имеет единственное решение (так как ее определитель 
). Решая ее (по теореме Крамера или методом Гаусса), получим x1=3, x3=3. Учитывая значения свободных неизвестных x2 и x4, получим частное решение неоднородной системы (1) 
.
5. Теперь осталось записать общее решение 
неоднородной системы (1): оно равно сумме частного решения этой системы и общего решения ее приведенной однородной системы (2): 
.
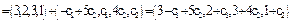Это значит: 
(7)
Мы получили общее решение системы (1) с помощью нескольких частных решений этой системы и ее приведенной однородной системы.
6. Проверка. Чтобы проверить, правильно ли вы решили систему (1), надо общее решение (7) подставить в (1). Если каждое уравнение обратится в тождество (с1 и с2 должны уничтожиться), то решение найдено верно.
Мы подставим (7) для примера только в последнее уравнение системы (1) (x1+x2+x3–9x4=–1).
Получим: 
.
.
Откуда –1=–1. Получили тождество.
Так поступаем со всеми остальными уравнениями системы (1).
Замечание. Проверка обычно довольно громоздкая. Можно рекомендовать следующую «частичную проверку»: в общем решении системы (1) произвольным постоянным придать некоторые значения и подставить полученное частное решение только в отброшенные уравнения (т.е. те уравнения из (1), которые не вошли в (5)). Если получите тождества, то, скорее всего, решение системы (1) найдено правильно (но полной гарантии правильности такая проверка не дает!). Например, если в (7) положить с2=-1, с1=1, то получим: x1=-3, x2=3, x3=-1, x4=0. Подставляя в последнее уравнение системы (1), имеем: 
, т.е. –1=–1. Получили тождество.
Пример 2. Найти общее решение системы линейных уравнений (1), выразив основные неизвестные через свободные.
Решение. Как и в примере 1, составляем матрицы A и системы (1) и исследуем систему (1) на совместность (см. пункты 1 и 2 примера 1). Так мы нашли общий базисный минор 
этих матриц. Оставляем теперь только те уравнения системы (1), коэффициенты из которых входят в этот базисный минор (т.е. у нас – первые два уравнения) и рассматриваем состоящую из них систему, эквивалентную системе (1):
. (5)
Перенесем в правые части этих уравнений свободные неизвестные:
. (8)
Систему (8) решаем по правилу Крамера, считая правые части свободными членами:
.
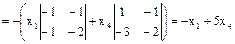Неизвестное x3 можно найти аналогично, а можно – из первого уравнения (подставив туда x2, найденное выше): x3=x2-1+x1-x4=-1+4x4.
Получим общее решение системы (1): x2=-x1+5x4, x3=-1+4x4. Здесь x1 и x4 могут принимать произвольные значения. Это решение можно записать и в виде вектора: (x1, -x1+5x4, -1+4x4, x4).
Замечание. Разумеется, систему (8) можно решать и другими способами – методом Гаусса, подстановкой. Но всегда правые ее части считаются свободными членами.
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ
Задание 1. Найти фундаментальную систему решений однородной системы и выразить через нее общее решение этой системы (способ выполнения этого задания описан в пункте 3 примера 1).
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 
Вариант 5. 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9. 
Вариант 10. 
Вариант 11. 
Вариант 12. 
Вариант 13.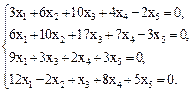 
Вариант 14. 
Вариант 15. 
Вариант 16. 
Вариант 17.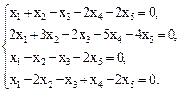 
Вариант 18. 
Вариант 19.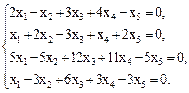 
Вариант 20. 
Вариант 21.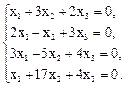 
Вариант 22. 
Вариант 23. 
Вариант 24. 
Вариант 25. 
Задание 2. Исследовать на совместность, найти общее решение системы линейных уравнений с помощью фундаментальной системы решений приведенной однородной системы и частного решения неоднородной системы. Сделать проверку (способ выполнения этого задания описан в примере 1).
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 
Вариант 5.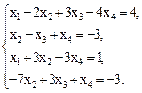 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9.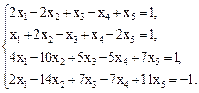 
Вариант 10. 
Вариант 11. 
Вариант 12. 
Вариант 13. 
Вариант 14. 
Вариант 15. 
Вариант 16. 
Вариант 17. 
Вариант 18. 
Вариант 19. 
Вариант 20. 
Вариант 21. 
Вариант 22. 
Вариант 23. 
Вариант 24. 
Вариант 25. 
Задание 3. Найти общее решение системы линейных уравнений из своего варианта задания 2, выразив основные неизвестные через свободные (способ выполнения этого задания описан в примере 2).
СОДЕРЖАНИЕ
ЛАБОРАТОРНАЯ РАБОТА № 1 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОД ГАУССА ИСКЛЮЧЕНИЯ НЕИЗВЕСТНЫХ-- 3
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ-- 7
ЛАБОРАТОРНАЯ РАБОТА № 2 КОМПЛЕКСНЫЕ ЧИСЛА-- 9
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ-- 15
ЛАБОРАТОРНАЯ РАБОТА №3 НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ МНОГОЧЛЕНОВ 19
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ-- 24
ЛАБОРАТОРНАЯ РАБОТА №4 КОРНИ МНОГОЧЛЕНОВ, КРАТНЫЕ МНОЖИТЕЛИ 26
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ-- 31
ЛАБОРАТОРНАЯ РАБОТА №5 ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ N-ГО ПОРЯДКА 34
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ-- 37
ЛАБОРАТОРНАЯ РАБОТА №6 МАТРИЦЫ--- 41
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ-- 45
ЛАБОРАТОРНАЯ РАБОТА №7 РЕШЕНИЕ ОДНОРОДНЫХ И НЕОДНОРОДНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ РАНГОВ ИХ МАТРИЦ-- 52
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ-- 58
Методическое издание
Алгебра
Лабораторные работы № 1-7
Составители: Маланьина Галина Александровна,
Хлебутина Валентина Ивановна,
Коневских Татьяна Михайловна.
Редактор Г.В. Тулякова
Корректор И.А. Михина
Подписано в печать. Формат 60´84 1/16.
Усл. печ. л. 3,95.
Уч.‑изд. л. 4,4. Тираж 500 экз. Заказ.
Редакционно-издательский отдел Пермского университета
614990. Пермь, ул. Букирева, 15
Типография Пермского университета.
614990. Пермь, ул. Букирева, 15
