Пусть дана матрица
,
где aij – некоторые числа. Будем её обозначать A=(aij).
Две матрицы A=(aij) и B=(bij) называются равными, если их размеры (число строк и число столбцов) совпадают и соответствующие элементы равны, т.е. при всех i, j: aij=bij.
Суммой двух матриц A=(aij) и B=(bij) одинаковых размеров называется матрица C=(cij) (что обозначается C=A+B) тех же размеров, элементы которой определяются равенствами для всех i, j: cij=aij+bij.
Произведением матрицы A=(aij) на число α называется матрица B=(bij) (что обозначается B=α∙A=A∙α), элементы которой определяются равенствами для всех i, j: bij=αaij.
Для этих операций справедливы следующие свойства:
1) A+B=B+A;
2) A+(B+C)=(A+B)+C;
3) 
0=(0), что A+0=A;
4) Для 
A (-A), что A+(-A)=0;
5) α (A+B)=αA+αB;
6) (α+β)A=αA+βA;
7) α(βA)=(α∙β)A.
Умножение матрицы A=(aij) на матрицу B=(bij) определяется только при условии, что число столбцов матрицы A равно числу строк матрицы B. Произведением матрицы A=(aij) на матрицу B=(bij) называется матрица C=(cij), элементы которой определяются равенствами: 
, i=1,2,…,m, j=1,2,…,n.
Таким образом, элемент матрицы C=AB, расположенный в i-ой строке и j-ом столбце, равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B.
Отметим основные свойства произведения матриц (считая, конечно, что все написанные произведения имеют смысл):
1) в общем случае AB≠BA;
2) A0=0A=0, где 0 – нулевая матрица;
3) AE=EA=A, где E – единичная матрица;
4) (A+B)C=AC+BC;
5) A(B+C)=AB+AC;
6) (AB)C=A(BC);
7) если A и B квадратные матрицы одного порядка, то det(AB)= detA∙detB.
Если A – квадратная матрица, то матрица B такая, что AB=BA=E, называется обратной относительно A и обозначается A-1, т.е. AA-1= A-1A=E.
Справедлива следующая теорема: Для того чтобы матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной (т.е. detA≠0).
Обратная матрица невырожденной матрицы A=(aij) единственная и имеет вид:
,
где Aij – алгебраическое дополнение элемента aij в detA, причём элементами i-ой строки матрицы A-1 являются алгебраические дополнения элементов i-го столбца матрицы A=(aij).
Пример 1. Найти матрицу, обратную матрице А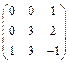 
.
Решение. Находим определитель матрицы А, ∆=detA= –3. Так как ∆≠0, то обратная матрица существует.
Находим алгебраические дополнения всех элементов матрицы A в определителе ∆. Напоминаем, что алгебраическое дополнение элемента aij находится по формуле Aij=(–1)i+jMij.
Для элементов матрицы A получаем
; 
;
; 
;
; 
;
A31= –3, A32=0, A33=0.
Составим обратную матрицу
.
Выражение AXB=C, AX=B, XA=B, где A,B,C – матрицы и X – неизвестная матрица, называется матричным уравнением.
Если матрица A невырожденная, то уравнения AX=B, XA=B имеют единственное решение, соответственно X=A-1B и X=BA-1. Если матрица A – вырожденная, то принимаем элементы матрица X за неизвестные, вычисляем произведение и приравниваем соответствующие элементы матриц левой и правой части уравнения.
Пример 2. Решить матричное уравнение 
.
Решение. Так как 
, то матричное уравнение имеет единственное решение 
. Находим обратную матрицу для матрицы 
. Так как A11=2, A12=-3, A21=-1, A22=2, поэтому 
, 
.
Проверка: 
, 
.
Получаем ответ: 
.
Пример 3. Найти все решения уравнения 
.
Решение. Для матрицы 
обратная матрица не существует. Запишем искомую матрицу в виде 
. Тогда данное уравнение примет вид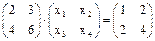 
или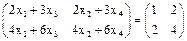 
.
Откуда получаем систему уравнений
Для нахождения ее решения достаточно найти решение системы
Эта система имеет бесчисленное множество решений
, где x3, x4 – любые числа.
Ответ: Данному уравнению удовлетворяет бесчисленное множество матриц вида 
, где x3, x4 – любые числа.
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ
Вариант 1
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все матрицы, перестановочные с матрицей 
.
4. Решить систему по правилу Крамера 
Вариант 2
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы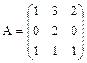 
.
3. Найти все решения матричного уравнения 
.
4. Решить систему по правилу Крамера 
Вариант 3
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все матрицы, перестановочные с матрицей 
.
4. Решить систему по правилу Крамера 
Вариант 4
1. Решить матричное уравнение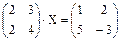 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все решения матричного уравнения 
.
4. Решить систему по правилу Крамера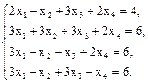 
Вариант 5
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все решения матричного уравнения 
.
4. Решить систему по правилу Крамера 
Вариант 6
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все решения матричного уравнения 
.
4. Решить систему по правилу Крамера 
Вариант 7
1. Решить матричное уравнение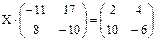 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все матрицы, перестановочные с матрицей 
.
4. Решить систему по правилу Крамера 
Вариант 8
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все решения матричного уравнения 
.
4. Решить систему по правилу Крамера 
Вариант 9
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все матрицы, перестановочные с матрицей 
.
4. Решить систему по правилу Крамера 
Вариант 10
1. Решить матричное уравнение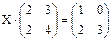 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все матрицы, перестановочные с матрицей 
.
4. Решить систему по правилу Крамера 
Вариант 11
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все матрицы, перестановочные с матрицей 
.
4. Решить систему по правилу Крамера 
Вариант 12
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы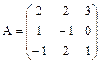 
.
3. Найти все матрицы, перестановочные с матрицей 
.
4. Решить систему по правилу Крамера 
Вариант 13
1. Решить матричное уравнение .
2. Найти обратную матрицу для матрицы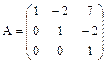 
.
3. Найти все матрицы, перестановочные с матрицей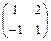 
.
4. Решить систему по правилу Крамера 
Вариант 14
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы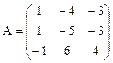 
.
3. Найти все решения матричного уравнения 
.
4. Решить систему по правилу Крамера 
Вариант 15
1. Решить матричное уравнение 
.
2. Найти обратную матрицу для матрицы 
.
3. Найти все решения матричного уравнения 
.
4. Решить систему по правилу Крамера 
