Определение 1. Если многочлен f(x) обращается в нуль при подстановке в него числа с вместо неизвестного, то с называется корнем многочлена f(x) (или уравнения f(x)=0).
Пример 1. f (x)=x5+2x3-3x.
Число 1 является корнем f(x), а число 2 не является корнем f(x), так как f(1)=15+2∙13-3∙1=0, а f(2)=25+2∙23-3∙2=42≠0.
Оказывается, корни многочлена связаны с его делителями.
Число с тогда и только тогда является корнем многочлена f(x), когда f(х) делится на х-с.
Определение 2. Если с - корень многочлена f(х), то f(х) делится на х-с. Тогда найдется натуральное число k, что f(х) делится на (х-с)k, но не делится на (х-с)k+1. Такое число k называется кратностью корня с многочлена f(х), а сам корень с - k-кратным корнем этого многочлена. Если k=1, то корень с называют простым.
Для нахождения кратности k корня с многочлена f(х) применяют теорему:
Если число с является k-кратным корнем многочлена f(х), то при k>1 оно будет (k-1)-кратным корнем первой производной этого многочлена; если же k=1, то с не будет служить корнем для f '(х).
Следствие. k-кратный корень многочлена f(х) впервые не будет служить корнем для k-й производной.
Пример 2. Убедиться, что число 2 является корнем многочлена f(х)=х4-4х3+16х-16. Определить его кратность.
Решение. Число 2 является корнем f(х), так как 24-4∙23+16∙2-16=0.
f '(x)=4x3-12x2+16, f '(2)=4∙23-12∙22+16=0;
f ''(x)=12x2-24x, f ''(2)=12∙22-24∙2=0;
f '''(x)=24x-24, f '''(2)=24∙2-24≠0.
Число 2 впервые не является корнем f'''(х), поэтому число 2 является трехкратным корнем многочлена f(х).
Пусть дан многочлен f(х) степени n≥1 со старшим коэффициентом 1: f(х)=хn+a1xn-1+…+an-1x+an и α1,...,αn – его корни. Корни многочлена и его коэффициенты связаны формулами, которые называют формулами Виета:
a1= -(α1+...+αn),
a2=α1α2+...+αn-1αn,
a3= -(α1α2α3+...+αn-2αn-1αn),
...........................
an=(-1)nα1α2...αn.
Формулы Виета облегчают написание многочлена по заданным его корням.
Пример 3. Найти многочлен, имеющий простые корни 2; 3 и двукратный корень –1.
Решение. Найдем коэффициенты многочлена:
а1=– (2+3–1–1)=-3,
а2=2·3+2·(–1)+2·(–1)+3·(–1)+3·(–1)+(–1)·(–1)= –3,
а3=– (2·(–1)·(–1)+3·(–1)·(–1)+3·2·(–1)+3·2·(–1))= –7,
а4=3·2·(–1)·(–1)=6.
Искомый многочлен есть х4–3х3–3х2–7х+6.
Определение 3. Многочлен f(х)ÌР[x] степени n приводим над полем Р, если он может быть разложен в произведение двух множителей φ(х) и ψ(х) из Р[x], степени которых меньше n:
f(x)=φ(x)ψ(x). (1)
f(x)ÎP[x] называют неприводимым над полем Р, если в любом его разложении на множители из Р[x] один из множителей имеет степень 0, другой – степень n.
Имеют место следующие теоремы:
Всякий многочлен ненулевой степени f(х) из кольца Р[x] разлагается в произведение неприводимых множителей из Р[x] однозначно с точностью до множителей нулевой степени.
Отсюда легко следует, что для всякого многочлена f(х)ÎР[x] степени n, n≥1, существует следующее разложение на неприводимые множители:
, (2)
где 
- неприводимые многочлены из P[x] со старшими коэффициентами, равными единице. Такое разложение для многочлена однозначно.
Неприводимые множители, входящие в такое разложение, не обязаны быть все различными. Если неприводимый многочлен встречается ровно k раз в разложении (2), то он называется k-кратным множителем многочлена f(х).Если множитель Р(х) входит в это разложение только один раз, то он называется простым множителем для f(х).
Если в разложении (2) одинаковые множители собрать вместе, то это разложение можно записать в следующем виде:
, (3)
где множители Р1(х),…,Рr(x) уже все различные. Показатели k1,…,kr здесь равны кратностям соответствующих множителей. Разложение (3) можно записать в виде:
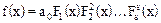, (4)
где F1(x) – произведение всех простых неприводимых множителей, 
- произведение всех двукратных неприводимых множителей и т.д. в разложении (3). Если в разложении (3) нет m-кратных множителей, то множитель 
считается равным единице.
Многочлены F1(x),…,Fs(x) для многочлена f(x) над числовыми полями можно найти, пользуясь понятием производной, алгоритмом Евклида из формулированной ранее теоремы (о связи с производной) следующим образом:
Отсюда
Поэтому получаем 
Таким образом, для многочлена f(x) мы можем найти множители 
.
Если для многочлена f(x) надо найти множители F1(x),…,Fs(x) его разложения (4), то говорят, что надо отделить его кратные множители.
Пример 4. Отделить кратные множители f(x)=х5-х4-5х3+х2+8х+4.
Решение. Находим НОД f(x) и f '(x)=5x4-4x3-15x2+2x+8.
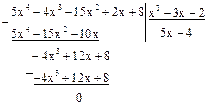
d1(x)=[ f(x), f '(x)]=x3-3x-2.
Теперь находим d2(x)=(d1(x), d1'(x)).
d2(x)=x+1.
Далее находим d3(x)=(d2(x), d2'(x)), d2'(x)=1,
d3(x)=1.
Выражаем v1(x), v2(x), v3(x).
(производим деление).
v1(x)=x2-x-2.
(производим деление).
Поэтому получаем F3(x)=v3(x)=x+1, 
Таким образом, многочлен f(x) имеет разложение f(x)=(х-2)2(х+1)3. В разложении (3) многочлена f(x) простых множителей нет, двукратный множитель х-2 и трехкратный множитель х+1.
Замечание 1. Этот способ ничего не дает в том случае, если все неприводимые множители многочлена f(x) простые (получим тождество f(x)=F1(x)).
Замечание 2. Этот способ позволяет определить кратности всех корней произвольного многочлена.
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ
Вариант 1
1. Убедиться, что многочлен 3х4-5х3+3х2+4х-2 имеет корень 1+i. Найти остальные корни многочлена.
2. Отделить кратные множители х5+5х4-5х3-45х2+108.
3. Найти многочлен наименьшей степени, корнями которого являются: 5, i, i+3.
Вариант 2
1. Чему равен показатель кратности корня х0=2 для многочлена f(x)=x5-7х4+12х3+16х2-64х+48? Найти остальные его корни.
2. Отделить кратные множители х5-6х4+16х3-24х2+20х-8.
3. Определить соотношение между коэффициентами уравнения x3+px+q=0, если его корни х1, х2, х3, удовлетворяют соотношению 
.
Вариант 3
1. Чему равен показатель кратности корня х0=4 для многочлена х4-7х3+9х2+8х+16? Найти остальные корни.
2. Отделить кратные множители х6-2х5-х4-2х3+5х2+4х+4.
3. Определить λ так, чтобы один из корней уравнения равнялся удвоенному другому: x3-7x+λ=0.
Вариант 4
1. Показать, что х=3 является корнем многочлена f(x)=х4-6х3+10х2-6х+9. Определить его кратность и найти остальные корни.
2. Отделить кратные множители многочлена х5+6х4+13х3+14х2+12х+8.
3. Сумма двух корней уравнения 2х3-х2-7х+λ=0 равна 1. Найти λ.
Вариант 5
1. Показать, что х0=-2 является корнем многочлена х4+х3-18х2-52х-40. Определить его кратность и найти остальные корни.
2. Отделить кратные множители многочлена f(x)=х5-5х4-5х3+45х2-108.
3. Найти многочлен наименьшей степени по данным корням 1, 2, 3, 1+i.
Вариант 6
1. Найти условие, при котором многочлен х5+ах4+b имеет двойной корень, отличный от нуля.
2. Отделить кратные множители многочлена х6+15х4-8х3+51х2-72х+27.
3. Многочлен а0хn+a1xn-1+…+an имеет корни х1, х2,…, хn. Какие корни имеют многочлены: 1) a0xn -a1xn-1+a2xn-2+…+(-1)nan;
2) anxn+an-1xn-1+…+a0?
Вариант 7
1. Показать, что х=-2 является корнем многочлена 4х5+24х4+47х3+26х2-12х-8. Найти кратность корня и найти остальные корни многочлена.
2. Отделить кратные множители многочлена х4+х3-3х2-5х-2.
3. Найти сумму квадратов корней уравнения 2х3-2х2-4х-1.
Вариант 8
1. Доказать, что х=1 является корнем многочлена х6-х5-4х4+6х3+х2-5х+2. Определить его кратность. Найти остальные корни многочлена.
2. Отделить кратные множители многочлена х5-3х4+4х3-4х2+3х-1.
3. Один из корней многочлена в два раза больше другого. Найти корни многочлена f(х)=х3-7х2+14х+λ.
Вариант 9
1. Найти условие, при котором многочлен х5+10ах3+5bх+с имеет тройной корень, отличный от нуля.
2. Отделить кратные множители многочлена х7-3х6+5х5-7х4+7х3-5х2+3х-1.
3. Решить уравнение х3-6х2+qх+2=0, если известно, что его корни образуют арифметическую прогрессию.
Вариант 10
1. Показать, что х=3 является корнем многочлена f(x)=х4-12х3+53х2-102х+72. Определить кратность корня, найти другие корни многочлена.
2. Отделить кратные множители многочлена х6-4х4-16х2+16.
3. Найти многочлен с действительными коэффициентами наименьшей степени по данным корням 1, 2+i, 3.
Вариант 11
1. Показать, что х=2 является корнем многочлена х5-6х4+13х3-14х2+12х-8. Найти его кратность и остальные корни.
2. Отделить кратные множители многочлена х4+х3-3х2-5х-2.
3. Составить многочлен наименьшей степени, если известны его корни х1=2, x2=1-i, x3=3.
Вариант 12
1. Показать, что х=-1 является корнем многочлена х4+х3-3х2-5х-2. Найти его кратность и остальные корни многочлена.
2. Отделить кратные множители многочлена х5-3х4+4х3-4х2+3х-1.
3. Составить многочлен наименьшей степени, если известны его корни х1=i, x2=2+i, x3=x4=2.
Вариант 13
1. Чему равен показатель кратности корня х0=4 для многочлена х4-7х3+9х2+8х+16? Найти остальные корни многочлена.
2. Отделить кратные множители многочлена х6-2х5-х4-2х3+5х2+4х+4.
3. Определить λ так, чтобы один из корней уравнения х3-7х+λ=0 равнялся удвоенному другому.
