Последовательность { xi }, i =0,1,… над полем действительных чисел называется линейной рекуррентной последовательностью (ЛРП) порядка п >0, если для некоторых действительных чисел a 1,…, an, a при любом i ³0
xi + п + a 1 xi + п -1+…+ an xi = a. (2.21)
ЛРП называется однородной (ОЛРП), если a =0, и неоднородной (НЛРП), если a ¹0. Равенство называют законом линейной рекурсии или линейным рекуррентным соотношением порядка п >0, а вектор (x 0,…, xп -1) – начальным вектором ЛРП. Последовательность { xi } есть решение линейного рекуррентного соотношения порядка п >0, если любые ее п +1 членов удовлетворяют закону рекурсии. Характеристическим многочленом ОЛРП называют связанный с законом линейной рекурсии многочлен F (x)= xn - a 1 xn -1-...- an -1 x - an.
Утверждение 2.1. Множество всех ОЛРП над полем действительных чисел, удовлетворяющих (2.21) при a =0, образует векторное пространство.
t Достаточно проверить, что множество указанных ОЛРП замкнуто относительно сложения и умножения на константу поля. u
Обозначим это пространство L. Далее потребуется понятие определителя матрицы M (обозначается det M), известное из курса линейной алгебры.
Теорема 2.8. Последовательности { ai (1)},…,{ ai ( n )} образуют базис в L Û det M ¹0, где
M=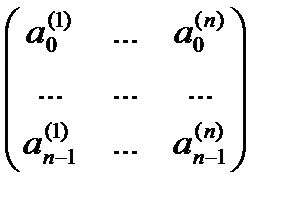 
. w
Решение линейного рекуррентного соотношения при a =0 может быть общим, т.е. записано как линейная комбинация базисных последовательностей с некоторыми коэффициентами b1,…,b n, и частным, т.е. последовательностью с заданными начальными условиями b =(a 0,…, aп -1). Во втором случае набор коэффициентов b=(b1,…,b n) определяется из решения системы линейных уравнений
M b= b.
Таким образом, основная задача – нахождение базиса пространства L.
Построение базисных последовательностей выполняется с помощью корней характеристического многочлена.
Лемма 2.3. Пусть l - ненулевой корень характеристического многочлена F (x). Тогда последовательность {l i }={1,l,l2,…} – решение однородного линейного рекуррентного соотношения (2.21).
t Подставим члены последовательности {l i } в однородное линейное рекуррентное соотношение (2.21). Так как l¹0, то получаем:
l i - a 1l i -1-...-l i - n +1 an -1-l i - n an =l i - n (l n - a 1l n -1-...-l an -1- an)= F (l)=0. u
Теорема 2.9. Пусть характеристический многочлен F (x) имеет n различных корней l1,…,l n, тогда последовательности {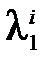 
},…,{ 
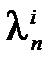} образуют базис в L.
t По лемме 2.3 все последовательности {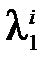 
},…,{ 
} принадлежат пространству L. Определитель, образованный первыми n элементами этих последовательностей, называемый определителем Вандермонда, равен:
= 
.
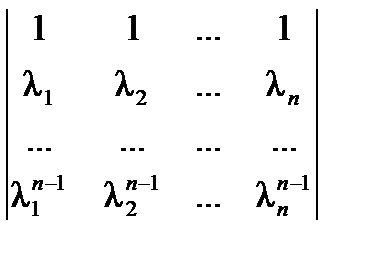Определитель не равен 0, так как все корни различны, значит, то теореме 2.8 последовательности { 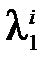},…,{ } образуют базис в L. u
Итак, если характеристический многочлен имеет n различных корней l1,…,l n, то общее решение однородного рекуррентного соотношения имеет вид:
{ xi }=b1{ 
}+…+b n {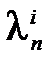 
}.
Если корни l1,…,l n – действительные, то все базисные последовательности также действительные. Если не все корни действительные, то комплексным корням соответствуют комплексные базисные последовательности. Вместе с тем, применяя определенное невырожденное преобразование к системе базисных векторов, можно получить новый базис действительных последовательностей (переход от базиса к базису рассмотрен в разделе 6.5).
Из теории полей известно, что комплексные корни действительного многочлена образуют пары сопряженных корней. Пусть пара сопряженных корней характеристического многочлена F (x) имеет вид: l1=r(cosj+ i sinj), l2=r(cosj- i sinj). Применим к базисным последовательностям невырожденное линейное преобразование
.
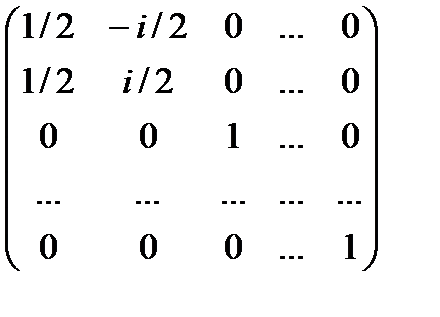Тогда паре базисных комплексных последовательностей {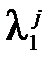 
}={r j (cos j j+ i sin j j)} и { 
}={r j (cos j j- i sin j j)} после преобразования соответствует пара базисных действительных последовательностей {r j cos j j} и {r j sin j j}. Следовательно, базис можно выбрать состоящим только из действительных последовательностей.
Теорема 2.10 [22]. Общее решение неоднородного рекуррентного соотношения есть сумма некоторого его частного решения и общего решения соответствующего однородного рекуррентного соотношения. w
Конечные автоматы
