Пусть X есть n -множество, P(X) - моноид всех преобразований множества X и S (X) - группа всех обратимых элементов моноида P(X), то есть группа всех подстановок множества X. Если X ¢ - также n -множество, то P(X)@P(X ¢) и S (X)@ S (X ¢). Это позволяет для любого n -множества рассматривать моноид - симметрическую полугруппу преобразований степени n, обозначаемую P n, и симметрическую группу Sn всех подстановокстепени n. Подгруппы группы Sn называют группами подстановок.
Теорема 4.6. Всякая полугруппа G порядка n изоморфна некоторой полугруппе преобразований (n +1)-множества.
t Пусть G ={ g 1,…, gn }. Положим X = G È{ g 0} и элементу gi полугруппы G поставим в соответствие преобразование j i множества X, i =1,…, n, называемое левым gi -сдвигом:
j i (g 0)= gi, j i (gj)= gi * gj, j =1,…, n.
Рассмотрим функцию f: G ®{j1,…,j n }, реализующую указанное соответствие. Функция f есть биекция, так как преобразования j1,…,j n попарно различны, это следует из того, что j i (g 0)¹j j (g 0) при i ¹ j. Пусть gjgi = gr для i, j Î{1,…, n }, тогда
f (gjgi)(g 0)= f (gr)(g 0)=j r (g 0)= gr = gjgi =j j (gi)=j j (j i (g 0))=(j j j i)(g 0)= f (gj) f (gi)(g 0),
f (gjgi)(gk)= f (gr)(gk)=j r (gk)= grgk = gjgigk =j j (gigk)=j j (j i (gk))=(j j j i)(gk)= f (gj) f (gi)(gk).
Значит, {j1,…,j n } - полугруппа преобразований и f (gjgi)= f (gj) f (gi). Следовательно, f – изоморфизм. u
Заметим, моноид G порядка n изоморфен некоторой полугруппе преобразований n -множества.
Теорема 4.7 (Кэли). Всякая конечная группа G порядка п изоморфна некоторой подгруппе группы Sn.
t Пусть е, g 1, g 2, …, gn -1 – все элементы группы G. Для фиксированного элемента а группы G рассмотрим отображение j а (g) =а * g. Имеем подстановку
j а = 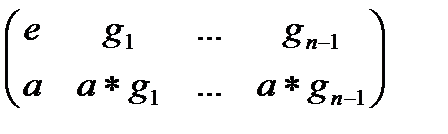 .
.
Вместе с тем, получаем отображение G ® Sn, при котором а ®j а. Убедимся, что это и есть искомый изоморфизм.
Во-первых, это отображение инъективно, так как различным элементам а и b группы G отвечают различные подстановки j а и j b (в первом случае е ® а, а во втором - е ® b).
Во-вторых, это отображение согласовано с операциями, то есть, j а * b (х) = j а ×j b (х)при любых а, b, х Î G. Действительно,
j а * b (х)= а * b * х,(j а ×j b)(х)=j а (j b (х))= а * b * х. u
Циклическая глубина и период преобразования g связаны с характеристиками графа Г(g).
Утверждение 4.2. Для g ÎP(X):
а) dep g есть наибольшая из длин всех подходов к циклам графа Г(g);
б) per g = НОК (l 1,..., lm), где l 1,..., lm - все различные длины циклов графа Г(g);
в) в частности, если g – подстановка,разлагающаяся в произведение циклов длины l 1,…, lk, то ord g = НОК (l 1,…, lk). w
Пусть G -полугруппа (группа) преобразований множества X и S ={ g 1,…, gp } - система образующих элементов полугруппы (группы) G, то есть G =á S ñ.
Пусть H – группа подстановок множества X. Преобразования g и h из P(X) называются сопряженными или подобными в группе H (при H = S (X) просто сопряженными или подобными), если в H найдётся подстановка d, при которой g =d-1× h ×d. По утверждению 4.3а отношение подобия относительно группы H, заданное на моноиде P(X), есть отношение эквивалентности.
Теорема 4.12. Преобразования g и h множества X подобны Û изоморфны графы Г(g) и Г(h) этих преобразований.
t а) Если преобразования g и h множества X подобны, то у = g (х) Û d(у)= h (d(х)) при некоторой подстановке dÎ S (X). Следовательно, графы Г(g) и Г(h)изоморфны, так как отличаются лишь переобозначением вершин с помощью подстановки d. Обратное утверждение доказывается рассуждениями в обратном порядке. u
Следствие. Подстановки g, h Î Sn сопряжены Û g и h имеют одинаковую цикловую структуру. w
Сопряженные подстановки имеют одинаковые порядки.
Пусть G £P(X). Элементы x, y Î X называются G – эквивалентными (обозначается x @ Gy), если g (x)= y и g ¢(y)= x для некоторых преобразований g, g ¢Î G.
Отношение @ G является отношением эквивалентности на X ¢.
Подмножества множества X ¢, образующие классы G –эквивалентности, называются областями транзитивности полугруппы G. Если G =á S ñ, где S ={ g 1,…, gp }, то области транзитивности полугруппы G суть компоненты сильной связности графа Г S (X).
Полугруппа преобразований G называется транзитивной, если X - ее единственная область транзитивности, и интранзитивной в противном случае. Орбитой элемента x Î X ¢ относительно полугруппы G (обозначается G (x)) называется область транзитивности полугруппы G, содержащая элемент x.
Циклическая полугруппа преобразований á g ñ типа (d, n) не транзитивна при d >1. Действительно, разбиение множества Х на непустые подмножества циклических и ациклических вершин графа Г(g ¢) одинаково для всех преобразований g ¢ полугруппы á g ñ, отсюда в á g ñ не найдется преобразования, отображающего любую циклическую вершину графа Г(g) в любую ациклическую вершину.
Стабилизатором элемента x в полугруппе (группе) преобразований G называется подмножество всех преобразований полугруппы (группы) G, для которых элемент x является неподвижным (обозначается St x (G)).
Отметим некоторые свойства стабилизатора элемента x в полугруппе преобразований G множества X.
1) Если St x (G)¹Æ при x Î X, то St x (G)£ G.
2) Если x @ Gy для x, y Î X, то g ¢ g ÎSt x (G) и gg ¢ÎSt y (G), т.е. St x (G)¹Æ Û x Î X ¢.
Пусть G – группа подстановок множества X. Элементы x, y Î X называются G – эквивалентными, если g (x)= y для некоторой подстановки g Î G. Данное отношение является отношением эквивалентности на X, так как каждый элемент X является циклическим в графе Г S (X). Классы G –эквивалентности называются областями транзитивности группы G. Если G =á S ñ, где S ={ g 1,…, gp }, то области транзитивности группы G суть компоненты связности в Г S (X). Группа подстановок G называется транзитивной (интранзитивной), если X – ее область транзитивности (X разбивается на две или более областей транзитивности). Орбитой элемента x Î X относительно группы G (обозначается G (x)) называется область транзитивности группы G, содержащая элемент x.
Обозначим через X [ k ] множество всех неупорядоченных бесповторных выборок размера k из алфавита X. Свойство транзитивности групп подстановок, определяющее переходы символов x, обобщается на свойство k -транзитивности (k - натуральное), определяющее возможность перехода любой выборки x ¢ в любую выборку y ¢, где x ¢, y ¢Î X [ k ].
Неупорядоченные бесповторные выборки (x 1,…, xk) и (y 1,…, yk) из X [ k ] называют G – эквивалентными (обозначается (x 1,…, xk)@ G (y 1,…, yk)), если g (xi)= yi для некоторой подстановки g Î G, i =1,…, k. Определенное отношение @ G является отношением эквивалентности на X [ k ].
Подмножества множества X [ k ], образующие классы G –эквивалентности, называются областями k - транзитивности группы G. Группа G называется k - транзитивной, еслиее единственная область k -транзитивности есть X [ k ], и k - интранзитивной в противном случае. Орбитой выборки (x 1,…, xk) относительно группы G (обозначается G (x 1,…, xk)) называют область k -транзитивности полугруппы G, содержащую эту выборку.
Свойство k -транзитивностигрупп допускает также вероятностную интерпретацию. Вероятностная мера задается на элементах группы, и возможность преобразования выборок характеризуется соответствующими вероятностями.
Теорема 4.13 (лемма Бернсайда). Для любого x Î X и любой подгруппы G группы S (X)
ô G ô=ôSt x (G)ô×ô G (x)ô.
Следствие. Для транзитивной группы G и любого x Î X:
ô G ô=ôSt x (G)ô×ô X ô. w
Теорема 4.14 [17, т.2, стр.282].Группа подстановок G является k -транзитивной Û G транзитивна и для некоторого x Î X является (k -1)-транзитивной подгруппа St x (G), рассматриваемая как группа подстановок множества X \{ x }. w






