Обозначим Rn - множество всех разбиений n -множества на непустые блоки, n >1. Для разбиений p,p¢Î Rn определим частичный порядок: p£p¢ Û p - продолжение разбиения p¢, то есть каждый блок разбиения p¢ есть либо блок разбиения p, либо объединение нескольких блоков разбиения p. Отношение p¢>¾p верно Û p¢ получено с помощью объединения любых двух блоков p. Ч.у.м. Rn есть решетка, называемая решеткой разбиений n -множества или решеткой эквиваленций на n -множестве.
Порядок решетки Rn есть число Белла Bn. Нуль решетки Rn - разбиение на n тривиальных блоков, единица решетки - само n -множество, отсюда длина решетки l (Rn)= n -1. Атомы Rn содержат лишь один нетривиальный двухэлементный блок. Коатомы содержат ровно 2 блока.
Заметим, что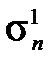 
= 
=1 при n >1 и 
= 
при n >2, где 
- числа Стирлинга 2-го рода. Тогда ï R 2ï= B 2=2, h (R 2)=1; ï R 3ï= B 3=5, h (R 3)=3. Если n >3, то > 
= 
при 1< k < n -1.
Различные разбиения n -множества на k блоков несравнимы, значит, ширина решетки Rn не меньше 
, отсюда при n >3 получаем оценки с использованием чисел Белла:
h (Rn)³ 
.
Отношение конгруэнтности
Систему представителей всех классов эквивалентности называют трансверсалом множества X по отношению А. Трансверсал множества по отношению эквивалентности в общем случае определен неоднозначно.
Рассмотрим алгебру A =(X, F), где X – основное множество, F ={ f 1,…, fm } – система определенных на X операций арности n 1,…, nm соответственно.
Отношение эквивалентности @ на X называется конгруэнцией на алгебре A, если оно согласовано со всеми операциями системы F, то есть если для xi, xi ¢Î X из отношений xi @ xi ¢, i =1,…, nj, при любом j =1,…, m следует
fj (x 1,…, 
)@ fj (x 1¢,…, ¢).
Гомоморфные образы абстрактной алгебры с точностью до изоморфизма определяются некоторыми конгруэнциями.
Теорема 3.1 [7, стр.181]. Пусть j - гомоморфизм алгебры A в алгебру B. Тогда отношение q такое, что x q x ¢ Û j(x)=j(x ¢), есть конгруэнция на алгебре A. w
Графы функций
Функции f: X ® Y, где X и Y - конечные множества мощности n и m соответственно, поставим в соответствие ориентированный двудольный граф Г(f)=(X È Y, U), где X È Y - множествовершин, U - множество дуг, и пара (x, y)Î U Û x Î X, y = f (x)Î Y. Граф Г(f) называют графом функции f.
Графом преобразования g п -множества X называют п -вершинный ориентированный графГ(g) с множеством вершин X и множеством дуг (x, g (x)).
Пусть S ={ g 1,…, gm } - система преобразований п -множества X. Графом системы преобразований S называют п -вершинный помеченный орграф Г(S)=Г(g 1)È…ÈГ(gm), в котором дуга (x, y) помечена максимальным подмножеством { i 1,…, is } множества {1,…, m } со свойством: gj (x)= y для любого j Î{ i 1,…, is }. Графу Г(S) биективно соответствует п -вершинный мультиграф, в котором имеется ровно s параллельных дуг (x, y) с метками i 1,…, is соответственно.
При l ³1 последовательность { x 1,…, xl } элементов множества X такая, что g (xl)= x 1и g (xi)= xi +1, i =1,…, l -1, образует цикл длины l в графеГ(g). Циклы имеются в графе любого преобразования конечного множества X, так как в последовательности { x, g (x), g 2(x),…} совпадения элементов неизбежны при любом x Î X. Неподвижному элементу преобразования g соответствует петля в Г(g).
В общем случае граф небиективного преобразования представляет собой совокупность нескольких независимых циклов, к которым могут иметься подходы, и по крайней мере к одному из циклов подход имеется. В силу однозначности преобразования g графГ(g) содержит лишьнезависимые простые циклы, число которых r удовлетворяет неравенствам: 1£ r £ n; если g не подстановка, то r < n. Каждый из независимых циклов вкупе со всеми имеющимися подходами к нему образует подграф графаГ(g), являющийся его компонентой связности. Таким образом, граф Г(g) есть объединение своих компонент связности.
Из каждой ациклической вершины графа Г(g) имеется ровно один подход к одному из циклов.
ГрафГ(g) подстановки g в силу инъективности подстановки не содержит подходов и состоит из k независимых циклов, 1£ k £ n, иначе говоря, каждая подстановка разлагается в произведение независимых циклов единственным образом с точностью до перестановки циклов [18, т.1, гл.XI, §8]. Для вычисления gt в степень t возводятся все циклы подстановки g.
Подстановка n -множества называется полноцикловой (п.ц.), если ее граф есть единственный цикл длины n.
Теорема 3.11. Число различных п.ц. подстановок n -множества равно (n -1)!.
t Полный цикл элементов n -множества X можно рассматривать как перестановку элементов множества, размещенную на n точках окружности. Значит, число различных полных циклов равно п!. В то же время циклы эквивалентны (реализуют одинаковые п.ц. подстановки) Û отличаются лишь параллельным сдвигом элементов по окружности. Каждый класс эквивалентности состоит из п циклов, тогда число различных п.ц. подстановок п -множества равно (п -1)!. u
