Дәрістің мақсаттары:
- энергия, жұмыс, қуат ұғымдарын меңгеру;
- энергияның әр түрін есептеу әдісін меңгеру.
Энергия - қозғалыс пен өзара әсерлесудің барлық түрлерінің универсал өлшеуіші
Материяның қозғалыс формалары өте көп. Оның ішіндегі ең қарапайымы – механикалық қозғалыс. Оны сандық түрде сипаттау үшін біз импульс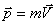 
ұғымын енгіздік. Жылулық қозғалыстың сандық сипаттамасы – температура болса, электр өрісінің сипаттамасы - 
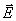кернеулік және т.б. Бұл шамалардың барлығы материяның әртүрлі қозғалыс формаларының сапалық ерекшеліктерін көрсетеді. Сондықтан материяның барлық қозғалыс формаларына қатысты және олардың өзара түрленуін көрсететін физикалық шаманы енгізу қажет. Физикадағы ортақ ұғымдардың бірі - энергия - осындай физикалық шама болып табылады.
Энергия - материяның әртүрлі қозғалыс формаларының ортақ өлшеуіші.
Қозғалыс материяның ажырамас бөлігі болғандықтан, кез келген жүйе энергияға ие болады. Жүйенің энергиясы жүйеде мүмкін болатын өзгерістерді (сандық және сапалық) сандық түрде сипаттайды. Энергия –күй функциясы.
Табиғатта механикалық қозғалыс арқылы энергиясы бір денеден басқа денеге берілетін процестер үздіксіз жүріп тұрады. Дененің механикалық қозғалысының өзгерісін оған басқа денелер тарапынан әсер етуші күштер тудырады. Өзара әсерлесуші денелер арасындағы энергия алмасу процесін сандық түрде сипаттау үшін берілген денеге түсірілген күштің жұмысын қарастырады. Жұмыс–энергияның күштік өзара әсерлесу процестерінде өзгеру шамасы.
Күштің жұмысы. Қуат
Массасы m қандай да бір бөлшекті қарастырайық. Оған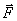 
күшпен әсер етейік. Осы бөлшек үшін Ньютонның екінші заңының теңдеуі
. (4.1)
(4.1) теңдеуін бөлшектің шексіз аз 
орын ауыстыру векторына көбейтсек ( = 
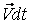екенін ескереміз)
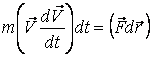. (4.2)
4.1 суреттен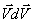 
скаляр көбейтіндісі
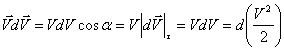
тең болады.
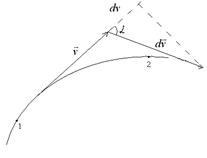
4.1 Сурет
Онда,
. (4.3)
(4.3) –тің оң жағындағы шама 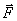күштің dA жұмысы деп аталады.
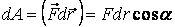, (4.4)
мұндағы α – 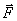күш пен 
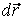орын ауыстырудың арасындағы бұрыш.
(4.4) формуласы 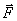күштің элементар жұмысын сипаттайды. Дене шекті қашықтыққа орын ауыстырғанда атқарылатын толық жұмыс қозғалыс траекториясы бойымен алынған қисық сызықты интеграл бойынша анықталады.
. (4.5)
Күш жұмысы – алгебралық шама, ол оң да, теріс те, нөлге де тең болуы мүмкін. Жұмыстың графиктік түрде анықталуы 4.2 суретте көрсетілген.
4.2 Сурет
Бірлік уақыт ішінде істелінген жұмысқа тең физикалық шама қуат деп аталады
. (4.6)
Бөлшектің және бөлшектер жүйесінің кинетикалық энергиясы
(4.3) теңдеуінің сол жағын қарастырайық. Ол қандай да бір функцияның толық дифференциалын береді.
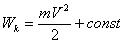. (4.7)
Wk шамасы бөлшектің кинетикалық энергиясы деп аталады. Кинетикалық энергия – толық энергияның бөлшектің қозғалысымен байланысты бөлігі. Тыныштықта тұрған дененің (V =0) кинетикалық энергиясы болмайтынын ескерсек, (4.7)-дан
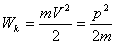(4.8)
тең екені шығады.
