Дәрістің мақсаты:
- статистикалық және термодинамикалық зерттеу әдістерінің маңыздылығын анықтау;
- классикалық статистикалық физиканың негізгі заңдарын оқып үйрену.
8.1 Зерттеудің статистикалық және термодинамикалық тәсілдері. Ықтималдылық
Молекулалық физика және термодинамика - молекулалар мен атомдардың орасан зор жиынынан тұратын денелердегі макроскопиялық процестерді зерттейтін физиканың бөлімі.
Молекулалық физикада зерттелетін жүйелер орасан көп бөлшектерден тұратыны ескерілетін болғандықтан, оларға механикада қолданылатын зерттеу әдістері жарамайды. Механикада әрбір дененің қозғалысын сипаттау үшін әрқайсысына қозғалыс теңдеуін жазып, кез келген уақыт кезеңіне сай бөлшектің координатын табамыз. Координаттың уақыт бойынша өзгеруін біле отырып, дененің жылдамдығын, үдеуін, импульсін және т.б. физикалық шамаларын анықтауға болады. Мысалы, газдың бір моліндегі молекулалардың қозғалысын сипаттау үшін 
теңдеу жазылып, шығарылуы қажет. Ол мүмкін емес. Тіпті біз осындай сан теңдеулерді шығардық делік, бірақ одан тұтас жүйені (затты) сипаттайтын қасиеттер жайында мағлұматтар ала алмаймыз. Молекулалық физика зерттейтін құбылыстар орасан көп молекулалардан құралған жүйелерде (денелерде, заттарда) болып өтетіндіктен, мұндай жүйелердің ерекшелігі мұнда дара молекулаға тән емес, тек жүйені ғана тұтас сипаттайтын қасиеттер пайда болады. Мұндай қасиеттерге, мысалы, қысым және температура жатады. Қысым мен температура тек бір ғана молекулаға қатысты деп айтуға болмайды. Осындай орасан көп бөлшектерден тұратын жүйелерді зерттеу әдістері де ерекше. Олар: молекула-кинетикалық немесе статистикалық және термодинамикалық әдістер деп аталады.
Денелердің әртүрлі қасиеттерін және зат күйінің өзгерістерін зерттеумен термодинамика шұғылданады. Алайда термодинамиканың молекула-кинетикалық теориядан айырмашылығы, ол - денелер мен табиғат құбылыстарының макраскопиялық суреттемесін ескермей, тек олардың макроскопиялық қасиеттерін ғана зерттейді. Термодинамиканың негізінде көптеген тәжірибелік деректердің жинағын жалпылау арқылы тағайындалған бірнеше негізгі заңдар жатыр (оларды термодинамиканың бастамалары деп атайды). Осы себептен термодинамиканың қорытындылары өте жалпы сипатта болады.
Статистикалық физика макроденелердің құрылымы жөніндегі атом-молекулалық көрініс моделі (мысалы, идеал газ моделі) және математикалық статистикаға негізделген. Макрожүйелердің қасиеті жүйені құрайтын бөлшектердің қасиеті бойынша, олардың қозғалысының ерекшеліктері және осы бөлшектердің динамикалық сипаттамаларының (энергия, жылдамдық және т.б.) орташа мәндері бойынша анықталады. Статистикалық физика орташа шамаларды есептеу әдістерін және олардың көмегімен жүйенің макропараметрлерін анықтауға үлкен мүмкіндік береді. Молекула-кинетикалық теорияның негізгі теңдеуі осындай жолмен алынған
, (8.1)
мұндағы p – газдың қысымы;
n – бірлік көлемдегі газ молекулаларының саны (молекула концентрациясы);
– молекулалардың ілгерілемелі қозғалысының орташа кинетикалық энергиясы.
Бұл теңдеу бойынша қысым бірлік көлемдегі молекулалардың ілгерлемелі қозғалысының кинетикалық энергиясының үштен екісіне тең болады.
Зат күйінің өзгерістерін әр түрлі көзқарас тұрғысында қарастыра отырып, термодинамика мен молекула-кинетикалық теория бір-бірін толықтырып, негізінен біртұтас ілім құрайды.
Максвелл бөлінуі
Газ молекулалары ретсіз, хаосты қозғалады. Қозғалыс бағытының ықтималдылығы бірдей, олардың қайсысының да басқаларынан ешбір артықшылығы жоқ. Сондықтан, молекулалардың бағыттары бойынша таралуы бір қалыпты болады.
Молекулалардың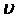 
жылдамдықтарының шамалары әртүрлі бола алады. Нөлден шексіздікке дейінгі аралықтағы жылдамдықтың мүмкін мәндерін бірдей ықтималды дей алмаймыз. Молекулалардың жылдамдығының соқтығысу кезінде өзгеруі кездейсоқ өтеді. Қайсыбір жеке молекула бірқатар жүйелі соқтығысқан сайын өз сыңарларынан энергия алып отыруы мүмкін, соның нәтижесінде оның энергиясы ε орташа мәнінен артып кетеді. Алайда газдың барлық молекулалары өз энергияларын жалғыз молекулаға беріп, өздері тоқталып қалады деп ойлағанның өзінде бұл молекуланың энергиясы, демек, оның жылдамдығы, шектеулі шамада болады. Сөйтіп, газ молекулаларының жылдамдығы қандай да бір 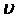-нан басталып ∞-пен бітетін мәндер қабылдай алмайды. Барлық молекулалардың қорытқы энергиясының едәуір үлесін бір молекулаға беретін процестер ықтималдылығы өте аз болады деп есептей отырып, мәні жылдамдықтың орташа мәнінен әлдеқайда артық жылдамдықтар да өте сирек кездеседі деген тұжырымға келеміз. Дәл осы тәрізді, соқтығысулар кезінде молекуланың жылдамдығы нөлге айналады деп те айтуға болмайды. Демек, жылдамдықтың орташа мәнімен салыстырғанда өте аз және өте үлкен жылдамдықтардың пайда болуының да ықтималдылығы өте аз болады, сонымен қатар 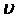-нің осы мәнінің ықтималдылығы 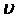→0 кезінде де, 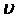→∞ кезінде де нөлге ұмтылады. Осы айтылғандардан, молекулалардың жылдамдықтары жылдамдықтың аса ықтимал мәнінің төңірегінде топтасатындығы шығады.
Жылдамдықтары белгілі, мысалы, 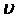1 және 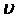2 жылдамдықтардың аралығында жататын молекулалардың саны туралы айтуға болады. Жылдамдықтар бойынша таралып бөлінуі туралы заңды бірінші рет Дж. Максвелл қорытып шығарды. Максвелл ықтималдық теориясын пайдаланып, 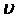мен +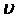 
жылдамдықтарының арасына жататын молекулалардың dN санынесептеп шығарған
, (8.2)
. (8.3)
Осылайша анықталған 
функциясы газ молекулаларының жылдамдықтар бойынша бөлінуін сипаттайды да бөліну функциясы деп аталады. Оның мәні мынада: функциясы жылдамдықтары жылдамдықтың 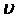берілген мәнінен бірлік интервалда жататын молекулалардың үлесін анықтайды. функциясы нормалау шартын 
қанағаттандырады.
Максвелдің бөліну функциясы 8.1 Суретінде көрсетілген және келесі формуламен өрнектеледі
. (8.4)
8.4 формуласынан көретініміз, бұл функцияның түрі газдың тегіне (молекула массасына) және күй параметріне (Т температурадан) тәуелді екенін көреміз.
Кез келген таңдап алынған молекуланың жылдамдығының 
интервалында жату ықтималдылығы 
тең.
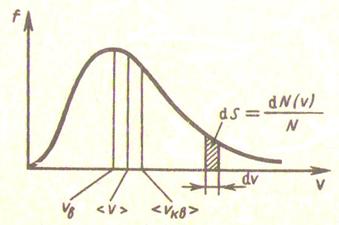
8.1 Сурет
Максвелл таралуының негізгі қасиеттері:
- молекулалардың өте аз үлесі ғана өте кіші және өте үлкен жылдамдықтарға ие болады;
- 
функциясының максимумына сәйкес келетін ықтималдық жылдамдық болады, сондықтан молекулалардың едәуір бөлігі 
жылдамдыққа жақын жылдамдықпен қозғалады
; (8.5)
- таралу қисығының симметриялы болмауына байланысты жылдамдығы 
-тан жоғары молекулалардың үлесі 
жылдамдықтағы молекулалар үлесіне қарағанда әрдайым жоғары болады. Бұл диспропорция температура артқан сайын күшейеді ( функциясы графигінде 
және 
-ге арналған қисықтар).
- таралу функциясын біле отырып, жылдамдыққа тәуелді кез келген физикалық шаманың орташа мәнін анықтауға болады.
Орташа арифметикалық жылдамдық
. (8.6)
Орташа квадраттық жылдамдық
; 
; 
. (8.7)
таралуы бөлшектердің бір-бірімен өзара қалай әсерлескеніне тәуелсіз. Ол тепе-теңдік күйдің орнығу процесінде бөлшектердің энергиямен алмасу қабілетімен анықталады.
Максвелл заңында қисықтың түрі температураға байланысты болады.Жүйенің температурасы жайлы жылдамдықтары Максвелл заңы бойынша таралатын жүйедегі бөлшектердің жылулық (хаосты) қозғалысы орныққан жағдайда айтуға болады.
