Егер зерттелетін жүйенің бастапқы мезетте күйі белгілі болған жағдайда, оның (материялық нүкте, материялық нүктелердің жиынтығы, қатты дене) кез келген уақыт мезетінде күйін анықтау – механиканың негізгі есебі болып табылады.
Классикалық механикада бөлшектің күйі берілген уақыт мезетінде оның үш координатасы (x,y,z) және импульстерінің проекциялары (рx, рy, рz)арқылы сипатталады.
Қатты дене әртүрлі күрделі қозғалыстарды жасай алады. Олардың барлығы екі қарапайым: ілгерілемелі және айналмалы қозғалыстардан тұрады. Қатты дененің ілгерілемелі қозғалысы массасы дененің массасына тең және инерция центріне орналасқан бөлшектің қозғалысына эквивалентті. Қатты дене бекітілген осьті айналып қозғалғанда дененің барлық нүктелері центрі осы осьте жататын шеңбер бойымен қозғалады. Бұл жағдайда дененің күйі осьті айналу бұрышы және бұрыштық жылдамдық арқылы беріледі.
1.1 Сурет 1.2 Сурет
Кез-келген М материялық нүктенің орны, О координат басы мен осы М нүктесін қосатын r радиус-вектормен сипатталады, яғни
. (1.1)
Егер материялық нүктенің декарт координаттарының уақытқа байланысы
х=х(t) y=y(t) z=z(t) (1.2)
берілген болса, онда материялық нүктенің қозғалысы толық анықталған. Бұл теңдеулер материялық нүкте қозғалысының кинематикалық теңдеулерідеп аталады. Олар нүкте қозғалысының бір ғана r( t) теңдеуінің баламасы болады.
Материялық нүкте (немесе дене) қозғалуы барысында сызатын сызығын траектория дейді. Траекторияның теңдеуін кинематикалық теңдеуден t параметрін аластау арқылы алуға болады. Траекторияның пішініне қарай қозғалыс: түзу сызықты және қисық сызықты болады.
Жүрілген жол берілген t уақыт ішіндегі барлық траектория бөліктерінің ұзындықтарының қосындысына тең болады.
Жылдамдық – берілген уақыт мезетіндегі қозғалыстың тездігін және оның бағытын сипаттайтын векторлық шама. Жылдамдықтың өлшеу бірлігі - м/с. Қарастырылып отырған нүктенің r радиус-векторынан уақыт бойынша алынған бірінші туынды лездік жылдамдық:
. (1.3)
Лездік жылдамдық векторы траекторияға қозғалыс бағытында жүргізілген жанама бойымен бағытталады.
Нүктенің t1 және t2 интервал аралығында жүрген жолы мына интегралмен
. (1.4)
есептеледі.
Үдеу – жылдамдықтың модулі және бағыты бойынша өзгеру тездігін көрсететін векторлық шама. Материялық нүктенің лездік үдеуі - қарастырылып отырған нүкте жылдамдығының уақыт бойынша алынған бірінші туындысына (осы нүктенің радиус-векторынан уақыт бойынша алынған екінші туындыға) тең векторлық шама:
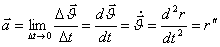. (1.5)
Үдеудің өлшеу бірлігі - м/с2. Жазық қисық сызықты қозғалыстың жалпы жағдайы үшін үдеу векторын екі құраушы үдеулердің векторлық қосын-дысы арқылы беру қолайлы:
. (1.6)
Мұндағы - тангенциал (немесе жанамалық) үдеу, ол жылдамдықтың модулі бойынша өзгеріс тездігін сипаттайды (1.1 суретті қара), яғни:
. (1.7)
Нормаль үдеу траекторияға оның қисықтық центріне қарай жүргізілген нормаль бойымен бағытталып, жылдамдық векторының бағыты өзгерісінің тездігін сипаттайды. Нормаль а n үдеудің шамасы шеңбер бойы- мен болатын қозғалыс жылдамдығы мен радиус шамасымен өрнектеледі
. (1.8)
Абсолют қатты дененің кинематикасы. Дененің айналмалы қозғалысы. Қозғалмайтын осьті айналу. Бұрыштық жылдамдық. Бұрыштық үдеу
Айналмалы қозғалысты сипаттау үшін R және φ полярлық координаттарын қолдану қолайлы, мұндағы R - радиус–полюстан (айналу центрінен) материялық нүктеге дейінгі қашықтық, ал φ – полярлық бұрыш (немесе бұрылу бұрышы).
Элементар бұрылуларды (Δφ немесе 
деп белгіленеді) псевдо-векторлар ретінде қарастыруға болады (1.2 суретті қара)
Бұрыштық орын ауыстыру - модулі бұрылу бұрышына тең, ал бағыты оң бұранданың ілгерілемелі қозғалысының бағытымен дәл келетін векторлық шама.
Бұрыштық жылдамдық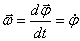 
. (1.9)
Бұрыштық үдеу 
. (1.10)
Бұрыштық жылдамдық ω векторы dφ векторы сияқты айналу осі бойымен, демек оң бұранда ережесі бойынша бағытталады. Бұрыштық үдеу ε векторы айналу осі бойымен бұрыштық жылдамдық векторының өсім-шесі жағына қарай (үдемелі айналғанда векторының бағыты векторымен бағыттас, ал баяу айналғанда - оған қарама-қарсы) бағытталады.
Бұрыштық жылдамдық пен бұрыштық үдеудің өлшеу бірліктері -рад/с және рад/ с2.
Нүктенің сызықтық жылдамдығының бұрыштық жылдамдық пен траектория радиусымен байланысы:
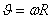. (1.11)
Бірқалыпты айналуда: 
, демек 
.
