Разработан проект подпорной бетонной стенки сложной формы, толщина которой равна 20 см. Чтобы заказать бетон, нужно определить объем, исходя из размеров. Стена имеет вид, приведенный на графике, рисунок 2.2.
Разбить эту задачу на следующие этапы:
1. Ввод в электронную таблицу размеров стенки;
2. Вычисление площади боковой поверхности верхней части стенки;
3. Вычисление площади нижней части стенки.
4. Вычисление суммарной площади боковой поверхности.
5. Умножить полученный результат на толщину стенки, чтобы вычислить объем.
Рисунок 2.2
Выполнить самостоятельно следующие практические примеры.
1. Работа, которую нужно затратить, чтобы растянуть пружину. С помощью устройства, изображенного на рисунке 2.3, можно определить, какая работа необходима для растяжения пружины. Устройство состоит из пружины, динамометра и линейки. Длина нерастянутой пружины равна 1,3 см. затем пружина постепенно растягивается. При каждом удлинении пружины на 0,4 см записывалось показание динамометра, в результате чего получился набор данных, приведенных в таблице. 2.1. Работа, необходимая для растяжения пружины, вычисляется по формуле:
А=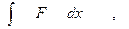 
(2.2)
где х – удлинение пружины.
Вычислить работу, которую нужно затратить, чтобы растянуть пружину от 0 до 3.6 см..
Рисунок 2.3
Таблица 2.1 Результаты опытов с пружиной
| Длина (см) | Исходная длина (см) | Удлинение (см) | Сила (Н) |
| 1.3 | 1.3 | 0.0 | 0.0 |
| 1.7 | 1.3 | 0.4 | 0.88 |
| 2.1 | 1.3 | 0.8 | 1.76 |
| 2.5 | 1.3 | 1.2 | 2.64 |
| 2.9 | 1.3 | 1.6 | 3.52 |
| 3.3 | 1.3 | 2.0 | 4.4 |
| 3.7 | 1.3 | 2.4 | 5.28 |
| 4.1 | 1.3 | 2.8 | 6.16 |
| 4.5 | 1.3 | 3.2 | 7.04 |
| 4.9 | 1.3 | 3.6 | 7.92 |
2. Энтальпия, необходимая для нагревания газа. Чтобы нагреть n молей газа от температуры Т1 до температуры Т2, необходимо затратить энтальпию, которая вычисляется с помощью теплоемкости газа по формуле:
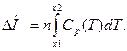(2.3)
Однако теплоемкость зависит от температуры. Для описания этой зависимости часто применяется уравнение, в правой части которого фигурирует полином третьего порядка относительно Т:
(2.4)
Зная значения коэффициентов a,b,c,d для определенного газа, можно вычислить теплоемкость этого газа при любом значении Т (в тех пределах, в которых работает уравнение (2.4). В таблице 2.2. приведены коэффициенты для нескольких распространенных газов (температура выражена в градусах Цельсия).
Таблица 2.2 - Коэффициенты для вычисления теплоемкости
| Название газа | a | b | c | d | Интервал применимости |
| Воздух | 28.94х10-3 | 0.4147х10-5 | 0.3191х10-8 | -1.965х10-12 | 0 – 1500 0 С |
| СО2 | 36.11х10-3 | 4.233х10-5 | -2.877х10-8 | 7.464х10-12 | 0 – 1500 0 С |
| СН4 | 34.31х10-3 | 5.469х10-5 | 0.3661х10-8 | -11.00х10-12 | 0 – 1500 0 С |
| Н2О | 33.46х10-3 | 0.6880х10-5 | 0.7604х10-8 | -3.593х10-12 | 0 – 1500 0 С |
(варианты: воздух, СО2, СН4, Н2О)
А) Вычислить теплоемкость газа в диапазоне температур от 200 до 800 0 С с шагом 20 0 С.
Б) Вычислить с помощью метода численного интегрирования энергию (изменение энтальпии), необходимую для нагревания 100 моль газа от 200 до 800 0 С.
С) Сравнить результат, полученный в пункте Б), с вычисленным аналитически. Для этого в интеграл из уравнения (2.3) подставить выражения для теплоемкости в виде полинома (2.4).
Контрольные вопросы
2.4.1 Перечислить формулы численного интегрирования.
2.4.2 Используя формулу прямоугольников для вычисления интеграла, сколько можно получить значений? С чем это связано?
2.4.3 В чем суть метода трапеций?
2.4.4 Какой из методов численного интегрирования дает более высокую точность?
2.4.5 Какой порядок имеет ошибка при применении метода трапеций?
2.4.6 В чем особенность метода Симпсона? Какие условия должны выполняться при использовании метода Симпсона?
2.4.7 Каков порядок ошибки при применении метода Симпсона?
2.4.8 Что означают «интервал между соседними точками» и «шаг интегрирования»?
2.4.9 Чему равен шаг интегрирования при применении метода Симпсона?
Варианты заданий
Задания выполнить, используя предложенные методы, на MS Excel, написать программу на одном из языков программирования (C++ или Pascal). Результаты сравнить.
| 
| ||
| 
| ||
|
| ||
| 
| ||
| 
| ||
|
| ||
|
|
| ||
|
| ||
|
| 
| ||
|
| 
| ||
|
| ||
|
| ||
|
|
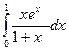
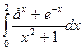
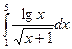
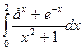
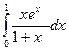
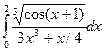
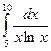
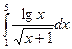
Задание 3. Метод наименьших квадратов
Цель работы: изучение методов математико-статистической и компьютерной обработки результатов экспериментов, испытаний и статистических наблюдений.
Для установления закономерностей при изучении многих природных явлений проводятся эксперименты или осуществляют сбор статистических данных об объекте исследования. После этого требуется определить функциональную зависимость между выбранными параметрами, описывающими изучаемое явление. Такую операцию называют аппроксимацией, полученную при этом функцию называют аппроксимирующей функцией, а ее график аппроксимирующей линией.
Пусть изучается связь между двумя переменными x и y; для этого рассматривается таблица значений этих переменных, полученных из эксперимента или в результате сбора данных:
A=(
(3.1)
B=(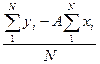
) (3.2)
3.1 Задание: изучается зависимость температуры от времени. Необходимо найти коэффициенты прямой линии, которая лучше всего описывает набор данных, введенных в столбцы х и у (рисунок 3.1).
Коэффициенты прямой А и В вычисляются по формулам (3.1), (3.2).
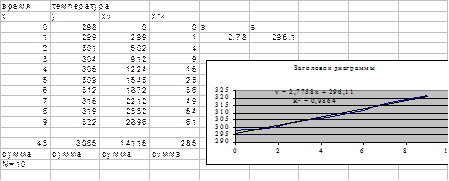
Рисунок 3.1
1.В ячейки А3:A12 (рисунок 3.1) вводятся значения времени, в В3:В12- температуры. В ячейке Е4 вычисляется коэффициент А по формуле (3.1), в F4 - коэффициент В по формуле (3.2).
2.Для определения углового коэффициента А, используя приемы регрессионного анализа в Excel, линии предназначена функция НАКЛОН(). Значение В можно найти с помощью функции ОТРЕЗОК.
Для этого установить курсор в ячейку Е5(F5) и выполнить действия:
Вставка – функции- статистические – НАКЛОН (ОТРЕЗОК) – выделяется столбец у(В3:В12), затем столбец х(А3:A12).
