Окне Поиск решения
Находясь на рабочем листе с разработанной вычислительной моделью, вызовем на выполнение надстройку "Поиск решения" (рис. 1.3).
В поле Установить целевую ячейку введем ссылку на ячейку, в которой будет рассчитываться значение целевой функции. Такой ячейкой на рабочем листе является ячейка G19, в которой заключена формула расчета стоимости плана перевозок. Так как стоимость плана необходимо минимизировать, то и переключатель Равной необходимо установить в положение минимальному значению (рис. 2.18).
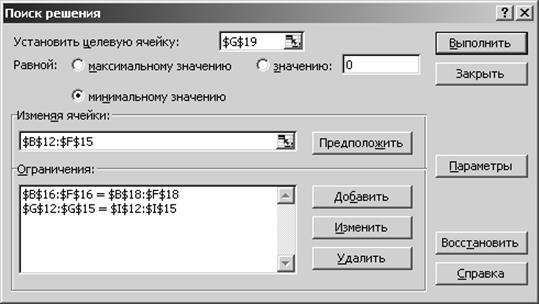
Рис. 2.18
В поле Изменяя ячейки введем ссылку на диапазон ячеек, в которых будут рассчитываться значения искомых переменных, т. е. на диапазон B12:F15.
В поле Ограничения введем ссылки на диапазоны G12:I15 и B16:F18, которые соответствуют выражениям (2.9) и (2.10).
В диалоговом окне Параметры поиска решения активизируем флажки Линейная модель и Неотрицательные значения.
Нажмем кнопку Выполнить – получим решение задачи (рис. 2.19).
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 50,00 | 50,00 | 0,00 | 0,00 | 250,00 | 350,00 | = | 350,00 | |
| Хр-ще2 | 0,00 | 0,00 | 200,00 | 0,00 | 0,00 | 200,00 | = | 200,00 | |
| Хр-ще3 | 300,00 | 0,00 | 50,00 | 100,00 | 0,00 | 450,00 | = | 450,00 | |
| Хр-ще4 | 0,00 | 350,00 | 0,00 | 0,00 | 0,00 | 350,00 | = | 350,00 | |
| лев. часть (завезено) | 350,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| знак | = | = | = | = | = | ||||
| прав. часть (потребн.) | 350,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 4250,00 | ® | min |
Рис. 2.19
План перевозок, рассчитанный в ячейках B12:F15, является оптимальным. При данном решении значение целевой функции, рассчитанное в ячейке G19, является минимальным и равно 4250 у.е.
Построенная модель классической транспортной задачи является платформой, на основе которой могут быть разработаны различные модифицированные модели, учитывающие разнообразные ситуации, возникающие в практической деятельности. Рассмотрим некоторые из них.
Увеличим потребности в ГСМ у первого центра до 500 тонн, а у второго центра до 650 тонн (см. ячейки B7 и C7 на рис. 2.20). Получим, что 
, 
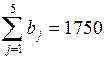, т. е. 
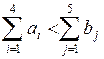. Таким образом, спрос превышает предложение, и задача стала несбалансированной. В такой ситуации для решения задачи обычно вводят фиктивного поставщика. При использовании надстройки "Поиск решения" в этом нет необходимости, надо только правильно расставить знаки в системе ограничений. Посмотрим, как это можно сделать в рассматриваемой задаче.
С точки зрения экономической интерпретации выражение 
означает, что все запасы должны быть вывезены, а выражение 
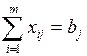–, что все потребности должны быть удовлетворены. В ситуации дефицита запасы будут вывезены полностью, т. е. выражение останется без изменений, а вот потребности будут удовлетворены не в полном объеме, т.е. уравнение 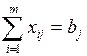трансформируется в неравенство 
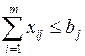. Обратим внимание, что используется знак нестрогого неравенства, так как какие-то центры могут быть обеспечены ГСМ в полном объеме, а какие-то нет.
После модификации математической модели задачи внесем соответствующие изменения в её вычислительную модель. Для этого на рабочем листе в диапазоне B17:F17 поменяем знаки "=" на "£"*, то же самое сделаем и в диалоговом окне Поиск решения. Нажмем кнопку Выполнить – получим решение модифицированной задачи (рис. 2.20).
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Запасы ГСМ в хр-щах, т | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | |||||
| Хр-ще1 | |||||||||
| Хр-ще2 | |||||||||
| Хр-ще3 | |||||||||
| Хр-ще4 | |||||||||
| Потребн. в ГСМ, т | |||||||||
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 100,00 | 0,00 | 0,00 | 0,00 | 250,00 | 350,00 | = | 350,00 | |
| Хр-ще2 | 0,00 | 0,00 | 200,00 | 0,00 | 0,00 | 200,00 | = | 200,00 | |
| Хр-ще3 | 350,00 | 0,00 | 0,00 | 100,00 | 0,00 | 450,00 | = | 450,00 | |
| Хр-ще4 | 50,00 | 300,00 | 0,00 | 0,00 | 0,00 | 350,00 | = | 350,00 | |
| лев. часть (завезено) | 500,00 | 300,00 | 200,00 | 100,00 | 250,00 | ||||
| знак | <= | <= | <= | <= | <= | ||||
| прав. часть (потребн.) | 500,00 | 650,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 4000,00 | ® | min |
Рис. 2.20
Обратим внимание, что ячейки диапазона G12:G15 равны ячейкам диапазона I12:I15, т. е. все запасы вывезены. Ячейки B16, E16 и F16 равны соответствующим ячейкам в диапазоне B18:F18, т. е. Центр1, Центр4 и Центр5 удовлетворены ГСМ в полном объеме, а ячейки C16 и D16 меньше соответствующих ячеек в диапазоне B18:F18, т. е. в Центр2 и Центр3 горюче-смазочные материалы недопоставлены в размере 250 и 50 тонн соответственно. Ниже мы рассмотрим, как в данной ситуации осуществить "справедливую" недопоставку ГСМ по всем центрам. А сейчас рассмотрим ещё ряд важных ситуаций, встречающихся на практике.
Важно! После получения решения в соответствии с рис.2.20 создайте копию данного листа (Щелчок правой кнопкой мыши по ярлычку листа – Переместить/скопировать лист… – (переместить в конец) – Создать копию – ОК). Продолжите решение задачи на листе Лист1(2).xls.
Допустим, вам поступило указание обеспечить Центр2 в полном объеме. Для этого необходимо лишь изменить в ячейке C17 знак "£" на знак "=" и ввести дополнительное ограничение С16=С18 в диалоговом окне Поиск решения. Решение представлено на рис. 2.21.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 0,00 | 100,00 | 0,00 | 0,00 | 250,00 | 350,00 | = | 350,00 | |
| Хр-ще2 | 0,00 | 200,00 | 0,00 | 0,00 | 0,00 | 200,00 | = | 200,00 | |
| Хр-ще3 | 350,00 | 0,00 | 0,00 | 100,00 | 0,00 | 450,00 | = | 450,00 | |
| Хр-ще4 | 0,00 | 350,00 | 0,00 | 0,00 | 0,00 | 350,00 | = | 350,00 | |
| лев. часть (завезено) | 350,00 | 650,00 | 0,00 | 100,00 | 250,00 | ||||
| знак | <= | = | <= | <= | <= | ||||
| прав. часть (потребн.) | 500,00 | 650,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 4850,00 | ® | min |
Рис. 2.21
Как видно из рис. 2.21, в Центр3 горюче-смазочные материалы вообще не доставляются. Допустим, вам поступило указание обеспечить Центр3 не менее чем на 85% от его потребностей. В математической интерпретации это указание запишется как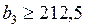 
. С учетом ранее имеющегося ограничения на потребность ГСМ в Центре3 будем иметь, что 
.
Ограничение 
в разработанной модели имеется, остается добавить ограничение 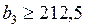. Это можно сделать различными способами, допустим, непосредственно в диалоговом окне Поиск решения ввести D16 >= 212,5. Решение представлено на рис. 2.22.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 0,00 | 100,00 | 0,00 | 0,00 | 250,00 | 350,00 | = | 350,00 | |
| Хр-ще2 | 0,00 | 0,00 | 200,00 | 0,00 | 0,00 | 200,00 | = | 200,00 | |
| Хр-ще3 | 137,50 | 200,00 | 12,50 | 100,00 | 0,00 | 450,00 | = | 450,00 | |
| Хр-ще4 | 0,00 | 350,00 | 0,00 | 0,00 | 0,00 | 350,00 | = | 350,00 | |
| лев. часть (завезено) | 137,50 | 650,00 | 212,50 | 100,00 | 250,00 | ||||
| знак | <= | = | <= | <= | <= | ||||
| прав. часть (потребн.) | 500,00 | 650,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 4875,00 | ® | min |
Рис. 2.22
В практической деятельности также встречаются задачи, связанные с блокированием перевозок. Это может быть обусловлено причинами техногенного характера (оползень, сход снега на перевал и т.п.), ремонтно-восстановительными работами (закрытие моста на реконструкцию и т.п.) или, что чаще встречается на практике, коммерческими соображениями.
Например, в плане на рис. 2.22 осуществляется перевозка по маршруту Хранилище2 – Центр3 в размере 200 тонн, необходимо заблокировать перевозку по данному маршруту. В математической интерпретации это указание запишется в виде ограничения 
. Другим, "искусственным", способом задания блокировки является назначение большой стоимости перевозки блокируемому маршруту, например, 
.
Используем первый способ для блокирования маршрута Хранилище2 – Центр3, для чего в диалоговом окне Поиск решения введем ограничение D13 = 0. Второй способ используем для блокирования маршрута Хранилище3 – Центр1, для чего в ячейку B5 введем какое-нибудь относительно большое число, например, 1000. Решение представлено на рис. 2.23.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 100,00 | 0,00 | 0,00 | 0,00 | 250,00 | 350,00 | = | 350,00 | |
| Хр-ще2 | 0,00 | 200,00 | 0,00 | 0,00 | 0,00 | 200,00 | = | 200,00 | |
| Хр-ще3 | 0,00 | 100,00 | 250,00 | 100,00 | 0,00 | 450,00 | = | 450,00 | |
| Хр-ще4 | 0,00 | 350,00 | 0,00 | 0,00 | 0,00 | 350,00 | = | 350,00 | |
| лев. часть (завезено) | 100,00 | 650,00 | 250,00 | 100,00 | 250,00 | ||||
| знак | <= | = | <= | <= | <= | ||||
| прав. часть (потребн.) | 500,00 | 650,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 5450,00 | ® | min |
Рис. 2.23
Другой распространенной задачей является задача перевозки определенного объема груза по указанному маршруту. Например, между Хранилищем4 и Центром1 заключен договор на поставку 300 т ГСМ, а между Хранилищем1 и Центром4 – на поставку 100 т ГСМ. Решение задачи представлено на рис. 2.24.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 0,00 | 162,50 | 0,00 | 100,00 | 87,50 | 350,00 | = | 350,00 | |
| Хр-ще2 | 0,00 | 200,00 | 0,00 | 0,00 | 0,00 | 200,00 | = | 200,00 | |
| Хр-ще3 | 0,00 | 237,50 | 212,50 | 0,00 | 0,00 | 450,00 | = | 450,00 | |
| Хр-ще4 | 300,00 | 50,00 | 0,00 | 0,00 | 0,00 | 350,00 | = | 350,00 | |
| лев. часть (завезено) | 300,00 | 650,00 | 212,50 | 100,00 | 87,50 | ||||
| знак | <= | = | <= | <= | <= | ||||
| прав. часть (потребн.) | 500,00 | 650,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 6900,00 | ® | min |
Рис. 2.24
И в заключение рассмотрим схему "справедливой" недопоставки в условиях дефицита, для чего обратимся к модели, представленной на рис. 2.20. Как видим, недопоставка коснулась только двух центров – Центра2 и Центра3, что является по отношению к ним несправедливым решением. Постараемся исправить сложившуюся ситуацию.
Важно! Схему «справедливой» недопоставки рассмотрите на листе Лист1.xls.
Самым простым решением в этом случае является равномерная недопоставка ГСМ во все пять центров. При дефиците в 400 тонн (400 = 1750 – 1350) она будет составлять 80 тонн ГСМ для каждого центра. Однако, как легко заметить, такое решение также будет несправедливым. Например, недопоставка в 80 тонн для Центра2 будет лишь "некоторой неприятностью", а для Центра4 – "бедой". Отсюда напрашивается пропорциональное распределение ГСМ относительно масштабов (потребностей) центров, что в нашем понимании и будет являться справедливым решением.
Существуют различные подходы к пропорциональному распределению ресурсов. Рассмотрим два из них.
Первый подход состоит в расчете коэффициента обеспеченности
.
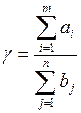Корректировка потребностей осуществляется в соответствии с формулой
,
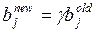где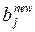 
– новое значение спроса в j -м центре;
– старое значение спроса в j -м центре.
Второй подход состоит в следующих, несколько более длинных рассуждениях. Вначале определяется доля каждого центра в общем объеме потребностей
.
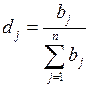Логичным будет в соответствии с этими долями осуществить и недопоставку:
,
где 
– объем недопоставки в j -й центр;
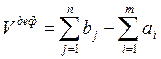– общий объем недостающих ресурсов (объем дефицита).
Корректировка потребностей осуществляется в соответствии с формулой
.
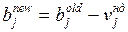Выбрав тот или иной способ корректировки потребностей, рассчитаем их новые значения. Все расчеты целесообразно проводить непосредственно на рабочем листе MS Excel. При этом заметим, что задача из несбалансированной вновь превращается в сбалансированную.
После внесения необходимых изменений на рабочем листе и в диалоговом окне Поиск решения запускаем процедуру поиска. Решение задачи представлено на рис. 2.25.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 12,86 | 144,29 | 0,00 | 0,00 | 192,86 | 350,00 | = | 350,00 | |
| Хр-ще2 | 0,00 | 7,14 | 192,86 | 0,00 | 0,00 | 200,00 | = | 200,00 | |
| Хр-ще3 | 372,86 | 0,00 | 0,00 | 77,14 | 0,00 | 450,00 | = | 450,00 | |
| Хр-ще4 | 0,00 | 350,00 | 0,00 | 0,00 | 0,00 | 350,00 | = | 350,00 | |
| лев. часть (завезено) | 385,71 | 501,43 | 192,86 | 77,14 | 192,86 | ||||
| знак | = | = | = | = | = | ||||
| прав. часть (потребн.) | 385,71 | 501,43 | 192,86 | 77,14 | 192,86 | ||||
| Стоимость перевозки | 4554,29 | ® | min |
Рис. 2.25
В рассмотренной задаче транспортировка ГСМ осуществлялась в условиях дефицита, т. е. выполнялось условие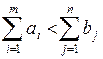 
. Наряду с "дефицитной" постановкой задачи возможна и противоположная ей "избыточная" постановка, т. е. когда выполняется условие 
. Исходные данные для такой задачи представлены на рис. 2.26.
Для решения этой задачи воспользуйтесь файлом Solver2(new).xls. Этот файл полностью (до адреса конкретной ячейки) соответствует примеру, рассмотренному в методических указаниях.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Запасы ГСМ в хр-щах, т | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | |||||
| Хр-ще1 | |||||||||
| Хр-ще2 | |||||||||
| Хр-ще3 | |||||||||
| Хр-ще4 | |||||||||
| Потребн. в ГСМ, т | |||||||||
Рис. 2.26
Как види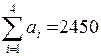м 
, 
, т. е. наблюдается избыток запасов ГСМ –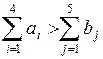 
. В данной ситуации потребности центров будут удовлетворены в полном объеме, т. е. имеет место ограничение 
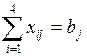(будем считать, что удовлетворение потребностей производится в объеме, не превышающем поданных заявок). В то же время запасы ГСМ будут вывезены из хранилищ не в полном объеме, т. е. имеет место ограничение 
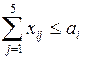(знак нестрогого неравенства указывает на то, что из некоторых хранилищ запасы могут быть вывезены в полном объеме, а из каких-то не в полном).
Решение задачи представлено на рис. 2.27.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 550,00 | 0,00 | 0,00 | 0,00 | 250,00 | 800,00 | <= | 850,00 | |
| Хр-ще2 | 0,00 | 50,00 | 250,00 | 100,00 | 0,00 | 400,00 | <= | 400,00 | |
| Хр-ще3 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | <= | 700,00 | |
| Хр-ще4 | 150,00 | 350,00 | 0,00 | 0,00 | 0,00 | 500,00 | <= | 500,00 | |
| лев. часть (завезено) | 700,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| знак | = | = | = | = | = | ||||
| прав. часть (потребн.) | 700,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 4450,00 | ® | min |
Рис. 2.27
Предположим, что поступила следующая информация:
а) Хранилище3 ликвидируется, поэтому запасы ГСМ должны быть вывезены из него в полном объеме;
б) мост по дороге от Хранилища2 к Центру3 закрыт на реконструкцию, поэтому необходимо запретить перевозку по указанному маршруту.
Решение задачи представлено на рис. 2.28.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 0,00 | 0,00 | 0,00 | 0,00 | 250,00 | 250,00 | <= | 850,00 | |
| Хр-ще2 | 0,00 | 150,00 | 0,00 | 100,00 | 0,00 | 250,00 | <= | 400,00 | |
| Хр-ще3 | 450,00 | 0,00 | 250,00 | 0,00 | 0,00 | 700,00 | = | 700,00 | |
| Хр-ще4 | 250,00 | 250,00 | 0,00 | 0,00 | 0,00 | 500,00 | <= | 500,00 | |
| лев. часть (завезено) | 700,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| знак | = | = | = | = | = | ||||
| прав. часть (потребн.) | 700,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 6300,00 | ® | min |
Рис. 2.28
Предположим, что неприкосновенный (неснижаемый запас) в Хранилище2 составляет 300 тонн. Тогда при емкости в 400 тонн из него в пределе может быть вывезено 100 тонн ГСМ.
Решение задачи представлено на рис. 2.29.
| A | B | C | D | E | F | G | H | I | |
| Хр-ща ГСМ | Центры распределения | Уравнения (неравенства) | |||||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | лев. часть (вывезено) | знак | прав. часть (запас) | ||
| Хр-ще1 | 150,00 | 0,00 | 0,00 | 0,00 | 250,00 | 400,00 | <= | 850,00 | |
| Хр-ще2 | 0,00 | 0,00 | 0,00 | 100,00 | 0,00 | 100,00 | <= | 400,00 | |
| Хр-ще3 | 450,00 | 0,00 | 250,00 | 0,00 | 0,00 | 700,00 | = | 700,00 | |
| Хр-ще4 | 100,00 | 400,00 | 0,00 | 0,00 | 0,00 | 500,00 | <= | 500,00 | |
| лев. часть (завезено) | 700,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| знак | = | = | = | = | = | ||||
| прав. часть (потребн.) | 700,00 | 400,00 | 250,00 | 100,00 | 250,00 | ||||
| Стоимость перевозки | 6450,00 | ® | min |
Рис. 2.29
Рассмотренные модели, безусловно, не перекрывают разнообразие всех тех многочисленных ситуаций, которые встречаются в практической деятельности. Тем не менее, их можно рекомендовать в качестве отправных точек для дальнейшего исследования. Направлениями таких исследований могут быть многопродуктовые перевозки, перевозки с промежуточными пунктами, перевозки с учетом грузоподъемности транспортных средств и многие другие. Ниже, развивая транспортную тематику, рассматривается известная разновидность задач линейного программирования, получившая название задачи о назначениях.
* В дальнейшем, если специально не оговорено, будет подразумеваться, что искомые переменные могут принимать только неотрицательные значения.
* Здесь и в дальнейшем речь будет идти о русскоязычных версиях Excel. В англоязычных версиях надстройка "Поиск решения" имеет название "Solver".
** Тем читателям, кто раньше не работал с Excel, мы настоятельно рекомендуем первоначально ознакомиться с основными техническими приемами работы с этой программой. Это не займет много времени и значительно ускорит прочтение не только этой книги, но и многих других, посвященных рассмотрению вопросов применения Excel в финансово-экономической практике.
* Некоторые аспекты неформальной теории принятия решений рассмотрены в п. 2.2.
* Изменение знаков на рабочем листе хотя и имеет лишь иллюстративный характер и не влияет на процедуру поиска решения, тем не менее, является очень полезным для понимания сути задачи и позволяет в последующем избежать ошибок при задании новых ограничений.
