Рассматриваемая задача является классической транспортной задачей или, другими словами, транспортной задачей закрытого типа, или сбалансированной транспортной задачей. Последнее название, на наш взгляд, является наиболее удачным, так как отражает условие сбалансированности запасов и потребностей, имеющееся в рассматриваемой задаче, т. е.:
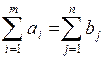, (2.2)
где m – количество исходных пунктов (в рассматриваемой задаче количество хранилищ);
n – количество пунктов назначения (в рассматриваемой задаче количество центров распределения);
ai – количество (объем) груза в i -м исходном пункте;
bj – количество (объем) груза, которое должно быть завезено в j -й пункт назначения.
Для рассматриваемой задачи имеем: 
, 
, т. е. 
, таким образом, она является сбалансированной.
Так как запасы равны потребностям, то все запасы будут вывезены, а все потребности будут удовлетворены. Данные условия можно записать в виде следующих уравнений:
, (2.3)
, (2.4)
где xij – искомые переменные задачи – количество (объем) груза, которое должно быть перевезено с i -го исходного пункта в j -й пункт назначения.
Так как количество перевозимого груза не может принимать отрицательные значения, то в рассматриваемой задаче имеет место условие неотрицательности, т. е.:
. (2.5)
Выражения (2.3)-(2.5) образуют систему ограничений задачи, целевая функция в которой задается выражением:
, (2.6)
где cij – стоимость перевозки одной единицы груза (в рассматриваемой задаче 1 т ГСМ) с i -го исходного пункта в j -й пункт назначения.
Экономическая интерпретация выражения (2.6) становится очевидной, если его записать в развернутом виде:
. (2.7)
Так как cij – это стоимость перевозки одной единицы груза с i -го исходного пункта в j -й пункт назначения, а xij – объем перевозимого груза по данному маршруту, то cij ´ xij – это стоимость перевозки груза по маршруту i -й исходный пункт – j -й пункт назначения. Сложение стоимостей перевозок по всем возможным маршрутам образует стоимость общего плана перевозок.
Объединяя выражения (2.3)-(2.6), получаем модель сбалансированной транспортной задачи:
, (1)
, (2) (2.8)
, (3)
. (4)
Опираясь на модель (2.8), разработаем математическую модель для рассматриваемой задачи.
Выражение (1) в модели (2.8) запишется в виде системы следующих уравнений:
,
, (2.9)
,
,
выражение (2) – в виде системы уравнений:
,
,
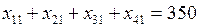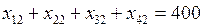, (2.10)
,
.
Условие неотрицательности (3) будет задано двадцатью неравенствами следующего вида:
, 
, …, 
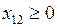. (2.11)
Целевая функция (4) запишется в виде выражения:
. (2.12)
Таким образом, математическая модель рассматриваемой задачи разработана, можно переходить к разработке вычислительной модели задачи на рабочем листе.
