с использованием надстройки "Поиск решения"
Как уже отмечалось, надстройка MS Excel "Поиск решения" может применяться для решения оптимизационных задач экономического анализа, что в общей схеме процесса принятия экономических решений может быть представлено фрагментом от блока "Разработка математической модели" до блока "Принятие решения" (рис. 1.6). Данный фрагмент в детализированном виде представлен на рис. 1.7.
С точки зрения пользователя MS Excel наибольший интерес на рис. 1.7 представляют прямоугольники с пунктирной линией. Таким образом обозначены на схеме сообщения, выдаваемые надстройкой "Поиск решения" в диалоговом окне Результаты решения задачи (рис. 1.8 – 1.10).
Так, если "Поиск решения" выдает сообщение "Решение найдено. Все ограничения и условия оптимальности выполнены" (рис. 1.8), то все в порядке, можно приступать к следующему этапу – анализу оптимального решения.
Ну а что делать, если выдано сообщение "Поиск не может найти подходящего решения" (рис. 1.10) или сообщение "Значения целевой ячейки не сходятся" (рис. 1.9)? "Надо скорректировать модель задачи или ввести дополнительные ограничения", – ответите Вы, посмотрев на рисунок 1.7. Да, действительно это так, но как это сделать осмысленно, а не наугад?
Чтобы ответить на этот вопрос, надо знать причину выдаваемых сообщений. И здесь, уважаемый читатель, опять-таки подтверждается истина, что нет ничего практичнее хорошей теории, так как прояснить суть данного вопроса позволяют следующие теоретические примеры из линейного программирования.
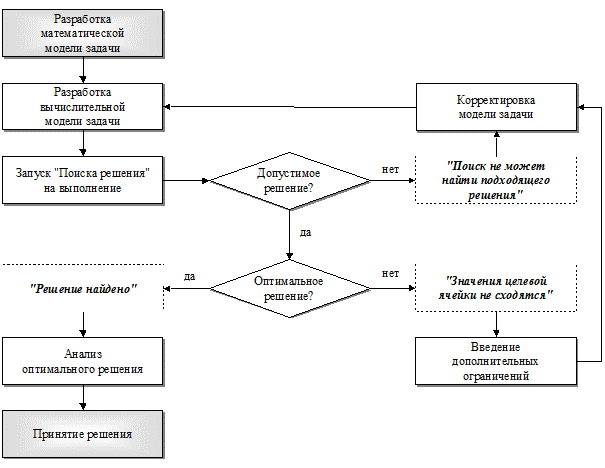
Рис. 1.7
Причину выдачи сообщения " Поиск не может найти подходящего решения " проиллюстрируем на примере (1.2):
, (1.2)
, 
.
Систему (1.2) представим графически (рис. 1.11). На рисунке видно, что нет таких значений x 1 и x 2, которые удовлетворяли бы системе (1.2). Значит, в данном примере область допустимых решений отсутствует. Про такую систему говорят, что ограничения несовместимы. К сожалению, это очень часто встречается на практике, а не только теоретически возможный вариант.
Рис. 1.8
Рис. 1.9
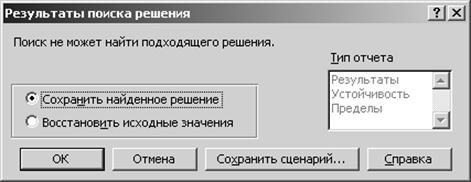
Рис. 1.10
Для преодоления несовместимости необходимо откорректировать математическую модель задачи. Например, в системе (1.2) одним из возможных вариантов является изменение ограничения на ограничение 
. В этом случае область допустимых решений системы (1.2) будет представлять собой треугольник, ограниченный прямым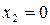и 
, 
и 
(рис. 1.12).
Рис. 1.11
Рис. 1.12
Причину выдачи сообщения "Значения целевой ячейки не сходятся" проиллюстрируем на примере (1.3):
, (1.3)
, .
Эта система показана на рис. 1.13, из которого видно – область допустимых решений не ограничена сверху. В таком случае при максимизации целевой функции (например, F = 2 x 1 + 3 x 2) решение получено быть не может, т.к. целевая функция, как и область допустимых решений, не ограничена сверху.
Рис. 1.13
Неограниченность целевой функции – это следствие ошибки в математической модели. Чтобы избежать таких ошибок, надо выполнять следующие правила:
1. При максимизации целевой функции она должна быть ограничена сверху с помощью ограничений, при этом модель с точки зрения содержания должна иметь вид:
(1.4)
2. При минимизации целевой функции она соответственно должна быть ограничена снизу, как это показано в (1.5):
(1.5)
Итак, уважаемый читатель, вот Вы и получили тот необходимый минимум теоретических сведений, который необходимо знать при решении оптимизационных задач экономического анализа с использованием надстройки MS Excel "Поиск решения". Но вместе с тем Вы, наверное, и сами это чувствуете, что в нашем изучении остался один очень существенный пробел – мы не показали примеры практического решения задач. А это – все равно что учиться плавать на берегу. Невозможно научиться решать задачи, не решая их. Поэтому, не откладывая в долгий ящик, советуем Вам переходить к изучению следующей главы.
Транспортная задача
Настоящий параграф посвящен вопросам разработки в MS Excel компьютерных моделей транспортного типа. Такие модели используются для составления наиболее экономичных планов перевозки продукции из нескольких пунктов отправления (например, склады) в несколько пунктов назначения (например, магазины). Транспортную модель можно также применять и при рассмотрении ряда других практических ситуаций, связанных с управлением запасами, составлением сменных графиков, назначением исполнителей по рабочим местам, оборотом наличного капитала и многими другими. Кроме того, модель можно видоизменять, с тем чтобы она учитывала перевозку нескольких видов продукции.
Широкое практическое приложение транспортной задачи обусловило её обязательное рассмотрение в курсе математического программирования высших учебных заведений. Можно предположить, что для многих читателей линейное программирование ассоциируется именно с решением транспортной задачи, рассмотрению которой уделено достаточно внимания в книгах по исследованию операций, экономико-математическому моделированию, логистике, экономическому анализу и некоторых других. Поэтому мы не будем подробно останавливаться на теоретических аспектах решения транспортной задачи, а сфокусируем свое внимание на вопросах разработки её компьютерной модели и последующего анализа различных практических ситуаций.
В качестве примера транспортной задачи рассмотрим задачу перевозки горюче-смазочных материалов (ГСМ).
Содержательная постановка задачи
Компанией разрабатывается план обеспечения потребителей горюче-cмазочными материалами. Исходные данные о запасах ГСМ в хранилищах, заявках на ГСМ в центрах распределения и стоимости перевозки 1 т ГСМ от хранилищ к центрам распределения представлены в нижеследующей таблице.
| Хранилища ГСМ | Центры распределения | Запасы ГСМ в хранилищах, т | ||||
| Центр1 | Центр2 | Центр3 | Центр4 | Центр5 | ||
| Хранилище1 | ||||||
| Хранилище2 | ||||||
| Хранилище3 | ||||||
| Хранилище4 | ||||||
| Потребность в ГСМ, т |
Требуется разработать такой план доставки ГСМ от хранилищ к центрам распределения, чтобы общая стоимость перевозок была минимальной.
