КАК ИНСТРУМЕНТАЛЬНОЕ СРЕДСТВО ПОСТРОЕНИЯ
1.1. Назначение надстройки "Поиск решения"
В своей практической деятельности экономистам-аналитикам нередко приходится сталкиваться с задачами, которые математик охарактеризовал бы как "оптимизационные задачи с наличием ограничений". В чем же заключаются отличительные особенности таких задач и каковы методы их решения? Прежде чем ответить на эти вопросы, рассмотрим несколько типовых примеров задач, принадлежащих данному классу.
Задача 1. Предприятие производит несколько видов продукции. Для производства каждого вида продукции требуется определенное количество материальных и трудовых ресурсов.
Известны ограничения на все виды ресурсов. Изготовление каждого вида продукции приносит определенную прибыль. Необходимо разработать такую производственную программу, при которой прибыль предприятия будет максимальной.
Задача 2. Компанией разрабатывается план обеспечения потребителей горюче-смазочными материалами (ГСМ). Известны запасы ГСМ в пунктах отправления и их потребности в пунктах назначения. Необходимо разработать такой план доставки ГСМ из пунктов отправления в пункты назначения, чтобы общая стоимость перевозок была минимальной.
Задача 3. Для производства продукции предприятие закупает листовой материал типовых размеров, из которого выкраиваются заготовки. Известны размеры заготовок и требуемое их количество. Необходимо так раскроить листовой материал, чтобы обеспечить минимум отходов.
Задача 4. В летно-испытательном центре проводится обучение летчиков на различных тренажерах и учебных самолетах. Стоимость одного часа занятий на тренажерах меньше, чем на самолетах, но и уровень подготовки обучаемых при обучении на тренажерах ниже по сравнению с уровнем обучения на самолетах. Известны продолжительность программы подготовки летчиков, требуемый уровень их обученности, лимиты расхода ресурса тренажеров и учебных самолетов. Требуется составить такой план подготовки летчиков, который позволил бы добиться требуемого уровня обученности при наименьших затратах.
Задача 5. Для проведения комплексной ревизии финансово-хозяйственной деятельности одного из соединений округа создана группа инспекторов-ревизоров. Известны перечень работ, которые необходимо выполнить в процессе ревизии, ожидаемая продолжительность каждой из этих работ и распределение их между исполнителями. Требуется составить график проведения ревизии, позволяющий выполнить весь комплекс работ в возможно короткий срок.
При всей разнородности перечисленных задач каждой из них присущи следующие свойства:
1) наличие альтернативных решений;
2) наличие цели;
3) наличие ограничивающих факторов.
Первое свойство указывает на то, что для каждой задачи существует как минимум два варианта её решения. Решение, которое в наибольшей степени способствует достижению цели, и является оптимальным.
Второе и третье свойства определяют характерную для всех перечисленных задач их общую (каноническую) постановку, которую можно представить следующим формальным образом:
найти оптимум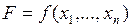 
(целевая функция задачи)
при (1.1)
, i = 1,…, m, (ограничения задачи)
.
Ограничение называется условием неотрицательности. Оно требует, чтобы переменные принимали только положительные или нулевые значения. Хотя, строго говоря, эти условия не являются обязательными, но в подавляющем большинстве случаев финансово-экономической практики они имеют место, что и обусловило их включение в представленную модель общего вида*.
Такая общность рассмотренных задач позволяет применить для их решения близкие по своей сути математические методы, которые достаточно широко представлены в такой научной дисциплине, как исследование операций (в частности в важнейшем её разделе математического программирования).
Изучение методов математического программирования давно включено в учебные программы всех экономических вузов, однако их реальное практическое применение всегда было сопряжено с рядом серьёзных трудностей, одной из которых являлось отсутствие "под рукой" соответствующего программного обеспечения. Лишь с появлением табличного процессора Excel 5.0 и его последующих версий (Excel 7/97/2000/2002/2003) вопрос о необходимом программном обеспечении оказался решенным. Теперь с полным основанием можно говорить, что "центр тяжести" в решении оптимизационных экономических задач полностью переместился от трудоемкой разработки вычислительных процедур их решения к творческой разработке их математических и вычислительных моделей. Это стало возможным благодаря включению в состав Excel дополнительной программы-надстройки "Поиск решения"*, позволяющей моделировать и находить решения практически для всех классов оптимизационных задач экономического анализа. О том, как работать с этой надстройкой, какие задачи экономического анализа могут быть решены с её помощью, как правильно составить вычислительную модель задачи и проанализировать её решение – обо всём этом мы и расскажем Вам в настоящем пособии.
1.2. Установка надстройки "Поиск решения"
Итак, Вы создали новую или открыли существующую книгу MS Excel. Перед Вами хорошо знакомое окно – мы на это надеемся** – активного рабочего листа. Где же находится надстройка "Поиск решения"? Для этого нам необходимо "посетить" меню Сервис. Здесь нас поджидают три возможных ситуации, действовать по которым надо следующим образом:
Рис. 1.1
Рис. 1.2
· ситуация №1 – в меню Сервис присутствует команда Поиск решения (рис. 1.1). Это "идеальная" ситуация, достаточно только щелкнуть указателем мыши на данной команде – и мы попадем в диалоговое окно надстройки;
· ситуация №2 – в меню Сервис отсутствует команда Поиск решения. Но пока еще рано расстраиваться, необходимо в этом же меню опуститься чуть ниже и выполнить команду Надстройки. Раскроется одноименное окно со списком доступных надстроек, установленных на Вашем компьютере (рис. 1.2).
В этом списке необходимо найти поле Поиск решения, активизировать перед ним флажок и нажать кнопку ОК. После этого в меню Сервис появится команда Поиск решения.
· ситуация №3 – в меню Сервис отсутствует команда Поиск решения, а в окне Надстройки нет поля Поиск решения. Это самая неприятная ситуация, так как без диска с дистрибутивом MS Office в этом случае не обойтись. Необходимо доустановить надстройку "Поиск решения" с диска.
Итак, уважаемый читатель, мы с Вами рассмотрели все возможные ситуации, связанные с установкой надстройки "Поиск решения". Если Вы её еще не установили, то поторопитесь, так как пора переходить к изучению элементов диалогового окна данной надстройки.
1.3. Диалоговое окно "Поиск решения"
Если в меню Сервис выбрать команду Поиск решения, то мы вызовем окно с одноименным названием (рис. 1.3).
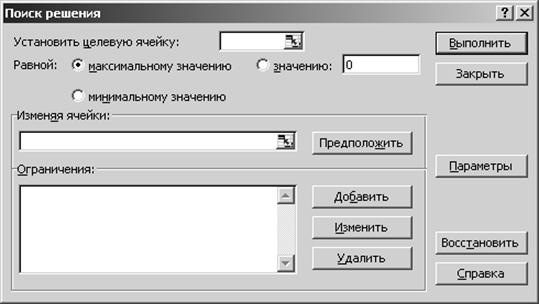
Рис. 1.3
Это окно является по существу той рабочей областью, в которой задаются параметры модели задачи, разрабатываемой пользователем на рабочем листе (о том, как разрабатывается модель оптимизации, будет рассказано ниже). Задание параметров модели задачи, а также условий и вариантов поиска решения осуществляется с помощью соответствующих элементов окна Поиск решения (кнопок, полей, флажков, переключателей и т.д.). В настоящем параграфе мы рассмотрим назначение этих элементов, а о том, как практически с ними работать, Вы узнаете при прочтении главы, посвященной вопросам разработки оптимизационных моделей экономических задач.
Основными элементами окна Поиск решения, описывающими вычислительную модель задачи, являются:
1. Поле Установить целевую ячейку и связанный с ним переключатель Равной: максимальному значению / минимальному значению / значению (с указанием конкретного значения в соответствующем поле). Поле Установить целевую ячейку указывает на ячейку, в которой содержится формула целевой функции модели. Переключатель Равной указывает на направление оптимизации (максимизация или минимизация) или устанавливает строго определенное значение, которое должна принять целевая функция. На практике обычно решаются задачи максимизации или минимизации.
В канонической постановке задачи оптимизации (1.1) полю Установить целевую ячейку и переключателю Равной соответствует выражение
найти оптимум .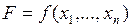
2. Поле Изменяя ячейки. Это поле указывает на диапазон изменяемых в модели ячеек. Вместе с ним связана кнопка Предположить, которую можно использовать для автоматического ввода с помощью Excel диапазона изменяемых ячеек. Однако, как показывает практика, всё же Excel иногда "ошибается" в решении этого вопроса, предлагая не совсем правильный диапазон ячеек. Поэтому мы рекомендуем самому вводить этот диапазон или внимательно проверять его после автоматического ввода с помощью кнопки Предположить.
В канонической постановке задачи оптимизации (1.1) полю Изменяя ячейки соответствуют переменные 
.
3. Поле Ограничения. Это поле указывает на ячейки, в которых содержатся формулы ограничений модели. Вместе с ним связаны кнопки Добавить, Изменить, Удалить, которые используются для работы с ограничениями модели в соответствии со своими названиями.
При нажатии кнопки Добавить вызывается окно Добавление ограничения (рис. 1.4), а при нажатии кнопки Изменить – Изменение ограничения (по интерфейсу это окно аналогично окну Добавление ограничения).
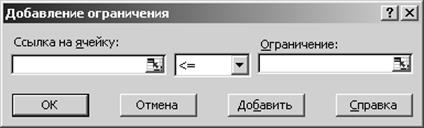
Рис. 1.4
В поле Ссылка на ячейку вводится адрес ячейки, содержащей левую часть уравнения (неравенства), а в поле Ограничение – адрес ячейки, содержащей правую часть уравнения (неравенства). В среднем поле выбирается знак ограничения, а также, если необходимо, указывается требование целочисленности переменных (для задач целочисленного программирования) или требование двоичности переменных (для задач булевого программирования).
В канонической постановке задачи оптимизации (1.1) полю Ограничения соответствуют выражения
, i = 1,…, m,
.
Замечание. В поле Ограничения можно не задавать условие неотрицательности x 1,…, xn ³ 0. Для задания этого условия достаточно активизировать флажок Неотрицательные значения в окне Параметры поиска решения (см. п. 1.4).
Кроме того, в состав окна Поиск решения входит пять кнопок:
· кнопка Выполнить запускает вычислительную процедуру поиска оптимального решения;
· кнопка Закрыть закрывает окно Поиск решения;
· кнопка Параметры вызывает окно Параметры поиска решения;
· кнопка Восстановить очищает окно Поиск решения;
· кнопка Справка вызывает раздел справочной системы MS Excel c краткой информацией об элементах диалогового окна Поиск решения.
В большинстве практических случаев для составления и решения вычислительных моделей задач достаточно использовать только вышеописанные элементы окна Поиск решения. Однако бывают ситуации, когда для поисковой процедуры необходимо указать некоторые дополнительные параметры. Для этого служит диалоговое окно Параметры поиска решения.
1.4. Диалоговое окно "Параметры поиска решения"
Окно Параметры поиска решения вызывается при нажатии кнопки Параметры в окне Поиск решения. На рис. 1.5 окно Параметры поиска решения показано со значениями элементов окна, установленных по умолчанию. Данные значения подходят для большинства практических задач и не требуют своего изменения. Дадим краткую характеристику элементов окна Параметры поиска решения.
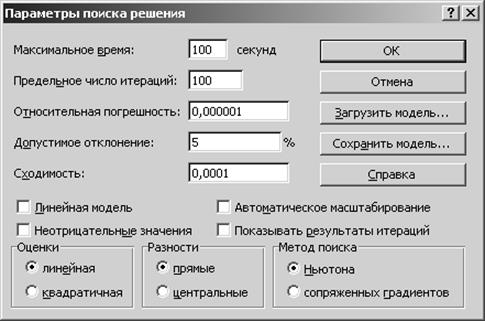
Рис. 1.5
1. Поле Максимальное время служит для ограничения времени, отпускаемого на поиск решения задачи. В это поле можно ввести время (в секундах), не превышающее 32767. Значение 100, используемое по умолчанию, подходит для решения большинства практических задач.
2. Поле Итерации служит для управления временем решения задачи, путем ограничения числа промежуточных вычислений (итераций). Значение 100, используемое по умолчанию, подходит для решения большинства практических задач.
3. Поле Точность служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Значение 0.000001, используемое по умолчанию, подходит для решения большинства практических задач. Более высокая точность увеличивает время, которое требуется для того, чтобы сошелся процесс оптимизации.
4. Поле Допустимое отклонение служит для задания допуска на отклонение от оптимального решения (в %) в задачах целочисленного программирования. Значение 5%, используемое по умолчанию, подходит для решения большинства практических задач. При указании большего допуска поиск решения заканчивается быстрее.
5. Поле Сходимость служит для задания величины относительного изменения значения в целевой ячейке за последние пять итераций. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Поле Сходимость применяется только к задачам нелинейного программирования. Значение 0.001, используемое по умолчанию, подходит для решения большинства практических задач. Лучшая сходимость требует больше времени на поиск оптимального решения.
6. Флажок Линейная модель служит для ускорения поиска решения задач линейного программирования или линейной аппроксимации задач нелинейного программирования.
7. Флажок Неотрицательные значения служит для задания условия неотрицательности для тех переменных, для которых оно не было установлено в поле Ограничения окна Поиск решения.
8. Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине – например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
9. Флажок Показывать результаты итераций служит для приостановки поиска решения для просмотра результатов отдельных итераций.
10. Переключатель Оценка служит для указания метода экстраполяции, используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Позиция Линейная (оценка) используется для линейной экстраполяции, а позиция Квадратичная (оценка) – для квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.
11. Переключатель Разности служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Позиция Прямые (производные) используется для нахождения производных гладких непрерывных функций, а позиция Центральные (производные) – для нахождения производных разрывных функций.
12. Переключатель Метод поиска служит для выбора алгоритма оптимизации. Позиция (метод) Ньютона служит для реализации квазиньютоновского метода, в котором запрашивается больше памяти, но выполняется меньше итераций, чем в методе сопряженных градиентов. Позиция (метод) Сопряженных градиентов служит для реализации метода сопряженных градиентов, в котором запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память.
13. Кнопка Загрузить модель служит для вызова диалогового окна Загрузить модель, в котором можно задать ссылку на область ячеек, содержащих загружаемую модель.
14. Кнопка Сохранить модель служит для вызова диалогового окна Сохранить модель, в котором можно задать ссылку на область ячеек, предназначенную для хранения модели оптимизации. Данный вариант предусмотрен для хранения на листе более одной модели оптимизации – первая модель сохраняется автоматически.
15. Кнопка ОК служит для закрытия окна Параметры поиска решения с сохранением изменений.
16. Кнопка Отмена служит для закрытия окна Параметры поиска решения без сохранения внесенных изменений.
Как уже было сказано выше, установленные по умолчанию значения элементов окна Параметры поиска решения подходят для решения большинства практических задач и не требуют своего изменения. Те случаи, в которых требуется изменить какое-либо значение, принятое по умолчанию, будут оговариваться нами дополнительно.
