Тема 1. 5 основные понятия и методы теории вероятностей и математической статистики.

Краткие теоретические сведения:

[1]: Гл.17, [2]: Гл.4.

Вероятностью событий A называется отношение числа исходов m, благоприятствующих наступлению данного события A, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.

. (1)

Вероятность любого события не может быть меньше нуля и больше единицы, т.е. . Невозможному событию соответствует вероятность P (A) = 0, а достоверному - P (A) = 1.

Теорема сложения вероятностей несовместных событий: Вероятность появления хотя бы одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

; (2)

. (3)

Теорема сложения вероятностей совместных событий: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.

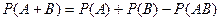. (4)

Для трёх совместных событий имеет место формула

. (5)

Событие, противоположное событию A (т.е. ненаступление события A), обозначают . Сумма вероятностей двух противоположных событий равна единице:

. (6)

Вероятность наступления события A, вычисленная в предположении, что событие B уже произошло, называется условной вероятностью события A при условии B и обозначается или .

Если A и B независимые события, то

. (7)

События A, B, C … называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.

Теорема умножения вероятностей независимых событий: Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

. (8)

Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле

. (9)

Теорема умножения вероятностей зависимых событий: Вероятность совместного появления двух независимых событий равна произведению одного из них на условную вероятность второго:

. (10)

На практике часто возникают ситуации, когда требуется определить вероятность события, которое может произойти с одним из несовместимых событий, образующих полную группу. Следующая теорема является следствием теорем сложения и умножения вероятностей и допускает нахождение вероятности полных событий.

Теорема: Вероятность события А, которое может наступить только при условии появления одного из событий H₁, H₂,…,H_n, образующих полную группу попарно несовместных событий, равна сумме произведений вероятностей каждого из них на соответствующую условную вероятность события А, т.е.

- формула полной вероятности

формула Байеса

Случайной величиной называется величина, которая в результате опыта может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.

Примеры случайных величин:

1. число выпавших гербов при пятикратном бросании монеты,
2. число бракованных изделий в случайно отобранной партии из 20 изделий,
3. дальность полета артиллерийского снаряда,
4. наружный диаметр трубы,
5. число мальчиков, родившихся за сутки в определенной стране.

В примерах 1,2,5 случайная величина может принимать отдельные изолированные значения, которые заранее можно перечислить. Так, в примере 1 такими значениями являются 0,1,2,3,4,5, в примере 2 – 0,1,2,3…20, в примере 5 – 0,1,2,3 …. Подобные случайные величины называются дискретными (прерывными).

Дискретной случайной величиной называют такую случайную величину, множество возможных значений которой либо конечное, либо бесконечное, но счетное.

Непрерывной случайной величиной называют такую случайную величину, которая может принять любое значение из некоторого конечного или бесконечного интервала.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Закон распределения случайной величины можно задать так же, как и в математическом анализе функцию одного аргумента, используя табличный, графический или аналитический способ задания. Рассмотрим первый из них. При табличном способе задания закона распределения первая строка таблицы содержит возможные значения случайной величины, а вторая – соответствующие вероятности.

 

х	х1	х2	…	хn
p	p1	p2	…	pn

Эта таблица называется рядом распределения.

Ряд распределения можно задать графически, если по оси абсцисс отложить возможные значения случайной величины, а по оси ординат – вероятности этих значений. Соединив точки (x_i; y_i) последовательно отрезками прямой линии, получим ломанную, которая называется многоугольником распределения.

Для решения многих практических задач совсем необязательно знать все возможные значения случайной величины и соответствующие им вероятности, а достаточно указать отдельные числовые параметры, которые позволяют в удобной форме отразить существенные особенности случайной величины, являющиеся не функциями, а числами, называют числовыми характеристиками.

Возможные значения случайной величины могут быть сосредоточены вокруг некоторого центра. Этот центр является некоторым средним значением случайной величины, вокруг которого группируются остальные ее значения. Для характеристики такой особенности распределения случайной величины служит математическое ожидание, которое иногда называют центром распределения или средним значением случайной величины.

Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений случайной величины на соответствующие вероятности появления этих значений, т.е.

Математическим ожиданием непрерывной случайной величины, возможные значения которой принадлежат отрезку , называется определенный интеграл

Если возможные значения случайной величины распределены по всей оси ох, то . Здесь предполагается, что несобственный интеграл сходится абсолютно, т.е. существует.

На практике также встречаются величины, имеющие одинаковые математические ожидания, но принимающие резко отличающиеся значения. У одних из этих величин отклонения значений от математического ожидания небольшие, а у других, наоборот, значительны, т.е. для одних рассеивание значений случайной величины вокруг математического ожидания мало, а для других оно велико.

Таким образом, математическое ожидание характеризует поведение случайной величины далеко не полностью.

Математическое ожидание квадрата отклонения случайной величины х от ее математического ожидания называют дисперсией случайной величины и обозначают D, т.е. .

Задание 1: Дискретная случайная величина задана следующим рядом распределения. Найти математическое ожидание случайной величины.

 

х
р	0,2	0,3	0,4	0,1

 

 

Решение:

Задание 2: Непрерывная случайная величина задана дифференциальной функцией распределения:

Найдите математическое ожидание этой случайной величины.

Решение:

Так как все возможные значения случайной величины расположены на отрезке от 1 до 3, то имеем: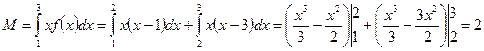

Предметом математической статистики является изучение случайных величин (или случайных событий) по результатам наблюдений. Для получения опытных данных необходимо провести обследование соответствующих объектов. Например, если исследователя интересует вероятность того, что диаметр валика определенного типоразмера после шлифовки окажется за пределами технического допуска, то надо знать закон распределения этого диаметра, а для этого, прежде всего надо располагать набором возможных значений диаметра. Однако обследовать все валики зачастую трудно, так как их количество может быть велико. Поэтому приходится из всей совокупности объектов выбирать только часть, т.е. проводить выборочное обследование. В некоторых случаях обследование объектов всей совокупности не имеет смысла, так как они разрушаются в результате обследования.

Совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений определенной случайной величины, или совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов, называется генеральной совокупностью.

Генеральную совокупность будем называть конечной или бесконечной в зависимости от того, конечна или бесконечна совокупность составляющих ее элементов.

Часть отобранных объектов из генеральной совокупности называется выборочной совокупностью или выборкой.

Для того, чтобы по выборке можно было достаточно уверено судить о случайной величине, выборка должна быть представительной (репрезентативной).

Репрезентативность выборки означает, что объекты выборки достаточно хорошо представляют генеральную совокупность. Можно осуществить два различных варианта выборки:

1. Каждая вынутая карточка возвращается назад в пачку, и карточки снова тщательно перемешиваются. Повторяя эту операцию, необходимое количество раз можно получить выборочную совокупность, которая называется случайной выборкой с возвратом.
2. Каждая вынутая карточка не возвращается назад в пачку. Образованная таким образом выборка называется случайной выборкой без возврата.

Так как при выборке с возвратом одну и туже карточку можно выбирать дважды, а значит, соответствующий объект придется обследовать также дважды, то эту выборку называют также случайной повторной. Аналогично, выборку без возврата называют случайной бесповторной.

Обычно полученные наблюдаемые данные представляют собой множество расположенных в беспорядке чисел. Просматривая это множество чисел, часто бывает трудно выявить какую-либо закономерность их варьирования (изменения). Для изучения закономерностей варьирования значений случайной величины опытные данные подвергают обработке.

Операция, заключающаяся в том, что результаты наблюдений над случайной величиной располагают в порядке неубывания, называется ранжированием опытных данных.

Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантом, а изменение этого значения - варьированием.

Для каждой группы сгруппированного ряда данных можно подсчитать их численность, т.е. определить число, которое показывает, сколько раз встречается соответствующий вариант в ряде наблюдений. Такие числа называют частотой варианта.

Численность отдельной группы сгруппированного рада наблюдаемых данных называется частотой или весом соответствующего варианта и обозначается m_i, где i – индекс варианта.

Отношение частоты данного варианта к общей сумме частот всех вариантов называется частостью или долей этого ряда и обозначается p_i.

Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов x_i с соответствующими им частотами m_i или частостями p_i.

Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частостями попаданий в каждый из них значений величины или частотами.

Таблица 1.

№ п.п.	Диаметр валика после шлифовки	Частота	Частость
	6,67 – 6,69		0.010
	6,69 – 6,71		0.075
	6,71 – 6,73		0.085
	6,73 – 6,75		0.220
	6,75 – 6,77		0.260
	6,77 – 6,79		0.220
	6,79 – 6,81		0.070
	6,81 – 6,83		0.055
	6,83 – 6,85		0.005
∑

 

Пусть имеется выборочная совокупность значений некоторой случайной величины Х объема n и каждому варианту из этой совокупности поставлена в соответствие его частость. Пусть, далее, х – некоторое действительное число, а m_х – число выборочных значений случайной величины Х, меньших х. Тогда число является частостью появления события Х<х. При изменении х в общем случае будет изменяться и величина . Это обозначает, что относительная частота является функцией аргумента х. А так как эта функция находится по выборочным данным, полученным в результате опытов, то ее называют выборочной или эмпирической.

Выборочной функцией распределения (функцией распределения выборки) называетсяфункция F(x), задающая для каждого значения х относительную частоту события Х<х.

1.

2. F(x) – неубывающая функция

3.

Построив вариационный ряд и изобразив его графически, можно получить первоначальное представление о закономерности, имеющих место в ряду наблюдений. Однако на практике зачастую этого недостаточно. Такая ситуация возникает, когда следует уточнить те или иные сведения о ряде распределения или когда имеется необходимость сравнить два или более ряда. При этом следует сравнивать однотипные вариационные ряды, которые получены при обработке сравнимых статистических данных. Например, можно сравнивать распределения длины втулок, изготовленных на двух однотипных автоматах, или распределения количества отказов определенных электронных устройств, изготовленных на разных заводах. Обычно графики таких распределений имеют почти одинаковый вид. Особенно это относится к кумулятивной кривой. Сравниваемые распределения могут существенно отличаться друг от друга. Они могут иметь различные средние значения случайной величины, вокруг которых группируются в основном остальные значения, или различаться рассеиванием данных наблюдений вокруг указанных значений и т.д. Поэтому для дальнейшего изучения изменения значений случайной величины используют числовые характеристики вариационных рядов. Поскольку эти характеристики вычисляются по статистическим данным, их обычно называют статистическими характеристиками или оценками.

Пусть собранный и обработанный статистический материал представлен в виде вариационного ряда. Теперь результаты наблюдений над случайной величиной следует подвергнуть анализу и выявить характерные особенности поведения случайной величины. Для этого удобнее всего выделить некоторые постоянные, которые представляли бы вариационный ряд в целом и отражали присущие изучаемой совокупности закономерности. Некоторые из этих постоянных отличаются тем, что вокруг них концентрируются остальные результаты наблюдений. Такие величины называются средними величинами. К ним относятся среднее арифметическое, среднее геометрическое, среднее гармоническое и т.д. Однако эти характеристики не отражают «величину изменчивости» наблюдаемых данных, например величину разброса значений признака вокруг среднего арифметического. Другими словами, упомянутые средние величины не отражают вариацию. Для характеристики изменчивости случайной величины, т.е. вариации служат показатели вариации. К ним относится размах варьирования R, среднее квадратическое отклонение, дисперсия и т.д.

Средним арифметическим наблюдаемых значений случайной величины Х называется частное от деления суммы всех этих значений на их число, т.е.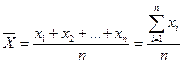

Выборочное дисперсией значений случайной величины Х называется среднее арифметическое квадратов отклонений наблюдаемых значений этой величины от их среднего арифметического, т.е.

Выборочным средним квадратическим отклонением называется арифметический корень из выборочной дисперсии, т.е.

Задание: По данным, приведенным в таблице 2, вычислим среднее арифметическое числа неправильных соединений в минуту.

 

Таблица 2:

Индекс	i
Число неправильных соединений в минуту	xi
Частота	mi
Частость	pi

Решение:

Среднее арифметическое вычислим по формул: 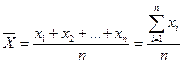. Имеем: ==2

Используя данные таблицы 1, вычислим выборочную дисперсию по формуле учитывая при этом, что =2, имеем: D==2.1