Тема 1. 3 основные понятия и методы линейной алгебры.

Краткие теоретические сведения:

Матрицей размера n x m, где n – это число строк, m – число столбцов, называется таблица чисел, расположенных в определенном порядке. Элементы матрицы обозначаются a_ij, где i – номер строки, j – номер столбца.

Матрица может состоять как из одной строки, так и из одного столбца и из одного элемента. Матрица, состоящая только из одной строки (только из одного столбца) называется матрицей-строкой или вектор-строкой (вектор-столбцом).

Если n=m, то матрица называется квадратной.

Матрица вида 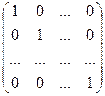= Е, называется единичной.

Если a_nm=a_mn, то матрица называется симметрической.

Квадратная матрица вида называется диагональной.

Матрица, все элементы которой выше или ниже главной диагонали равны нулю, называется треугольной.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Данные операции определены только для матриц одинакового размера.

Операции умножения (деления) матрицы на произвольное число (≠0) число сводятся к умножению (делению) каждого элемента матрицы на это число.

Произведением матрицы называется матрица, элементы которой могут быть вычислены как сумма произведений элементов i-той строки первой матрицы на элементы j-ого столбца второй матрицы.

Умножение матриц не коммутативно, т.е. АВ≠ВА. Но, если для каких либо матриц АВ≠ВА, то матрицами называются перестановочными.

Умножение матриц справедливо, если число столбцов первой матрицы равно числу строк второй матрицы.

Матрицу В называют транспонированной матрице А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

Определителем квадратной матрицы называется число, которое может быть вычислено по элементам матрицы с помощью миноров и алгебраических дополнений по теореме: «Определитель матрицы равен произведению элементов какой-либо строки или какого-либо столбца на соответствующие алгебраические дополнения этих элементов».

Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.

Определитель единичной матрицы равен 1.

Определитель матрицы второго порядка равен разности произведений элементов главной и побочной диагоналей.

Определитель треугольной матрицы равен произведению элементов главной диагонали.

Минор произвольного элемента 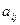квадратной матрицы равен определителю матрицы, полученному из исходного вычеркиванием i – ой строки и j – го столбца.

Алгебраическим дополнением называется минор матрицы, умноженный на (-1) в степени, равной сумме номеров строк и столбцов минора матрицы.

Определитель матрицы обладает следующими свойствами:

1. Определитель не меняется при транспонировании матрицы.
2. Определитель суммы матриц равен сумме определителей матриц.
3. Определитель произведения матриц равен произведению определителей матриц.
4. При перестановке двух строк или двух столбцов матрицы определитель поменяет знак, не изменившись по абсолютной величине.
5. Если какую-либо строку или столбец матрицы умножить на отличное от нуля число, то и определитель умножится на это число.
6. Определитель, содержащий две пропорциональных строки или два пропорциональных столбца равен нулю.
7. Определитель, содержащий две одинаковых строки или два одинаковых столбца равен нулю.

8. Определитель, содержащий нулевую строку или нулевой столбец равен нулю.

9. Определитель не изменится, если к элементам какой-либо строки или столбца прибавить элементы другой строки или столбца, умноженные на одно и то же, отличное от нуля число.

Задача 1. Вычислите определитель матицы A=

Решение:

Det=

Элементарными преобразованиями матрицы называют следующие преобразования:

1. умножение строки на число, отличное от нуля;
2. прибавление к одной строке другой строки;
3. перестановка строк;
4. вычеркивание одной из одинаковых строк;
5. транспонирование.

Данные операции применимы и для столбцов.

Если существуют квадратные матицы Х и А, удовлетворяющие условию: ХА=АХ=Е, где Е – единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается 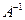, причем .

Задача 2. Найдите обратную матрицу для матрицы

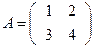
Решение:

detA=4-6=-2

A₁₁=4, A₁₂=-3, A₂₁=-2, A₂₂=1

Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A).

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований. Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

На основе матриц разработаны различные методы решения задач. Например, матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Пусть дана система уравнений:

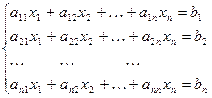
Составим матрицы:

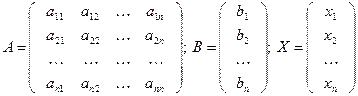
Систему уравнений можно записать: АХ=В

Задача 3. Решите систему уравнений:

Решение:

Найдем обратную матрицу :

detA=-30 (для матрицы А вычисление определителя можно производить по правилу треугольника)

А₁₁=5, А₁₂=10, А₁₃=-5, А₂₁=-1, А₂₂=14, А₂₃=-19, А₃₁=-1, А₃₂=-16, А₃₃=11

Решением системы является тройка чисел: 1;2;3.

Формула Крамера: (для невырожденных или неособенных матриц) 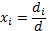, где –определитель матрицы, полученный из данного заменой i-ого столбца матрицы столбцом свободных членов, 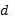– определитель матрицы системы.

Метод Гаусса – метод последовательного исключения неизвестных. Правило Крамера и матричный метод неприменимы в тех случаях, когда система имеет бесконечно много решений или несовместна, а метод последовательного исключения неизвестных в любом случае приведет к ответу! Процесс решения системы уравнений методом Гаусса, состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому виду, путем последовательного исключения переменных. На втором этапе решения (обратный ход) последовательно находят переменные из получившейся ступенчатой системы. На каждом шаге решения справа располагается расширенная матрица, эквивалентная системе уравнений.

Для решения СЛАУ по схеме единственного деления Гаусса произведем следующие преобразования:

Рассмотрим СЛАУ четвертого порядка:

Будем исключать неизвестное x₁ из всех уравнений системы(1), кроме первого.

x₁ – ведущее неизвестное

a₁₁ – ведущий коэффициент

a₁₁ ≠ 0

Разделим первое уравнение на a₁₁:

x₁+ + + =

Обозначим a₁₂/a₁₁ = b₁₂, … a₁₅/a₁₁ = b₁₅

bij= aij/a11

x₁ + b₁₂x₂ + b₁₃x₃ + b₁₄x₄ = b₁₅ (2)

x₁ = b₁₅ – b₁₂x₂ – b₁₃x₃ – b₁₄x₄

Для исключения х₁ произведем следующие преобразования:

из второго уравнения (1) вычтем (2) умноженное на а₂₁:

(a₂₂-a₂₁b₁₂)x₂+(a₂₃ – a₂₁b₁₃)x₃+(a₂₄ – a₂₁b₁₄)x₄ = (a₂₅-a₂₁b₁₅)

 

Обозначим a₂₂-a₂₁b₁₂ = a₂₂⁽¹⁾

a₂₃ – a₂₁b₁₃ = a₂₃⁽¹⁾…

получим a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + a₂₄⁽¹⁾x₄ = a₍¹⁾₂₅

a(1)ij=aij-ai1*b1j

По аналогии из третьего уравнения (1) вычитаем (2) умноженное на а₃₁, после преобразования получим:

а₃₂⁽¹⁾ х₂+ а₃₃⁽¹⁾ х₃ + а₃₄⁽¹⁾ х₄ = а₃₅⁽¹⁾

Аналогично из четвертого уравнения (1) вычитаем (2) умноженное на а₄₁:

а₄₂⁽¹⁾х₂ + а₄₃⁽¹⁾х₃+а₄₄⁽¹⁾х₄=а₄₅⁽¹⁾

В результате получим: (1)¹

Далее, ≠0 – ведущий коэффициент.

В результате исключения х₂из всех уравнений (1)⁽¹⁾, кроме первого получим:

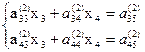(1)², где

aij(2)=aij(1)-ai2(1)*b2j(1)

 

Далее алгоритм повторяется, пока не получим последнее неизвестное.

Задача 4. По схеме единственного деления Гаусса решите систему:

Решение:

Х1	Х2	Х3	Х4	с.ч
		-1 -1 -3 -2
		-0,5	0,5
	-1 -3	-0,5	0,5	-2 -4
		-1
		-2 -0,5	0,5
				-1
			0,5	-0,5
				-1
			х4=-1 х3=-1 х2=1 х1=1