ѕр€ма€ может быть задана как пересечение двух плоскостей. ¬ этом случае она задаетс€ системой уравнений, определ€ющих эти плоскости:
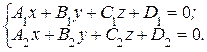 (6)
(6)
аноническое уравнение пр€мой:
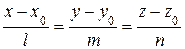 . (7)
. (7)
«десь ћ (x 0, y 0, z 0) Ц точка, через которую проходит пр€ма€, (l, m, n) Ц направл€ющий вектор пр€мой.
Ёто уравнение на самом деле представл€ет собой систему двух уравнений, как и в формуле (6). ќдин или два знаменател€ могут быть равны 0, это будет означать, что соответствующие числители приравниваютс€ к 0.
”равнение пр€мой, проход€щей через две данные точки ћ 1(x 1, y 1, z 1), ћ 2(x 2, y 2, z 2):
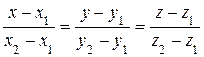 . (8)
. (8)
ѕример 1.7.1. ¬ пространстве заданы точки A (3, 2, Ц1), ¬ (2, Ц1, 2) — (1, 3, 4), D (4, Ц5, 5). а) постройте уравнение плоскости (ј¬—); б) Ќайдите рассто€ние от точки D до плоскости (ј¬—); в) постройте уравнение пр€мой ј—; г) постройте уравнение перпендикул€ра к плоскости (ј¬—), проход€щего через точку D.
–ешение. а) ¬оспользуемс€ формулой (4):
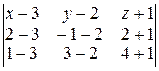 = 0;
= 0;
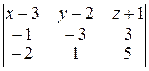 = 0;
= 0;
(x Ц 3)(Ц15 Ц 3) Ц (y Ц 2)(Ц5 + 6) + (z + 1)(Ц1 Ц 6) = 0;
Ц18(x Ц 3) Ц (y Ц 2) Ц 7(z + 1) = 0;
Ц18 x + 54 Ц y + 2 Ц 7 z Ц 7 = 0;
Ц18 x Ц y Ц 7 z + 49 = 0;
18 x + y + 7 z Ц 49 = 0.
б) ¬оспользуемс€ формулой (5):
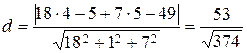 .
.
в) ¬оспользуемс€ формулой (8):
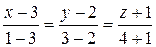 ;
;
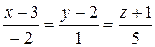 .
.
г) Ќаправл€ющим вектором перпендикул€ра €вл€етс€ нормаль к плоскости; из пункта а) это 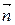 = (18, 1, 7). ¬оспользуемс€ формулой (7):
= (18, 1, 7). ¬оспользуемс€ формулой (7):
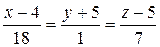 .
.
” п р а ж н е н и €
1.7.1. ¬ пространстве даны точки ј (1; 3; 0), B (Ц1; 2; 1), C (Ц2; 1; 3), D (2; 2; 1).
а) ѕостройте уравнение плоскости ј¬—;
б) ѕостройте уравнение пр€мой ¬—;
в)ѕостройте уравнение перпендикул€ра, проведенного к плоскости ј¬— через точку D;
г) Ќайдите рассто€ние от точки D до плоскости ј¬—;
д) ѕостройте уравнение плоскости, проход€щей через точку D параллельно плоскости ј¬—.
ѕреобразование координат
 „асто дл€ определени€ вида и параметров фигуры, задаваемой уравнением в некоторой системе координат, бывает удобно перейти к другой системе координат. Ёто может упростить уравнение.
„асто дл€ определени€ вида и параметров фигуры, задаваемой уравнением в некоторой системе координат, бывает удобно перейти к другой системе координат. Ёто может упростить уравнение.
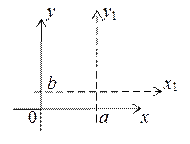
ѕростейшее преобразование Ц это параллельный перенос координатных осей. ѕусть новые координатные оси x 1 и y 1 имеют в старых координатах уравнени€ x = a, y = b. “огда новые координатные оси выражаютс€ через старые формулами x 1 = x Ц a, y 1 = y Ц b, а старые через новые формулами x = x 1 + a, y = y 1 + b. Ќапример, уравнение окружности с центром в точке ј (a, b) и радиусом r в старых координатах имеет вид (x Ц a)2 + (y Ц b)2 = r 2, а в новых x 12 + y 12 = r 2.
ƒругой вид преобразований системы координат Ц это поворот координатных осей вокруг начала координат на угол a (угол отсчитываетс€ против часовой стрелки). ‘ормулы перехода от старой системы к новой задаютс€ уравнени€ми
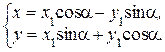
‘ормулы перехода от новой системы к старой задаютс€ уравнени€ми
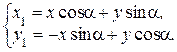
ћожно использовать и косоугольную систему координат, в которой оси расположены под произвольным углом и длины единичных отрезков по ос€м абсцисс и ординат различны. ¬ такой системе пр€мые линии и многие другие фигуры задаютс€ уравнени€ми тех же типов, что и в пр€моугольной, но параметры уравнений измен€ютс€; становитс€ весьма проблематично определ€ть рассто€ни€ и углы. Ќо использование косоугольной системы координат позвол€ет упрощать преобразование уравнений в тех случа€х, когда требуетс€ определить только тип фигур, задаваемых этими уравнени€ми. ѕреобразование координат производитс€ по формулам
|
|
|
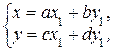
где ad Ц bc ¹ 0.
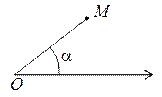 —овершенно другой вид системы координат, отличный от декартовой, Ц это пол€рна€ система координат. ќна задаетс€ точкой (полюсом) ќ и пол€рной осью Ц лучом, выход€щим из полюса. ѕоложение любой точки ћ на плоскости задаетс€ углом a, который луч ќћ образует с пол€рным лучом, и радиус-вектором r Ц длиной отрезка ќћ. Ёти два параметра полностью определ€ют положение точки ћ. ѕри этом радиус-вектор определ€етс€ однозначно, а угол с точностью до периода 2p: этот период соответствует полному обороту вокруг полюса, привод€щему к тому же направлению. Ќапример, уравнение окружности с центром в полюсе и радиусом R в пол€рной системе имеет вид r = R.
—овершенно другой вид системы координат, отличный от декартовой, Ц это пол€рна€ система координат. ќна задаетс€ точкой (полюсом) ќ и пол€рной осью Ц лучом, выход€щим из полюса. ѕоложение любой точки ћ на плоскости задаетс€ углом a, который луч ќћ образует с пол€рным лучом, и радиус-вектором r Ц длиной отрезка ќћ. Ёти два параметра полностью определ€ют положение точки ћ. ѕри этом радиус-вектор определ€етс€ однозначно, а угол с точностью до периода 2p: этот период соответствует полному обороту вокруг полюса, привод€щему к тому же направлению. Ќапример, уравнение окружности с центром в полюсе и радиусом R в пол€рной системе имеет вид r = R.
ќт декартовой к пол€рной системе координат можно перейти по формулам x = r cos a, y = r sin a. ќбратный переход производитс€ с помощью формул
r = 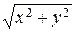 ;
;
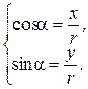
ривые второго пор€дка
”равнение второго пор€дка Ц это уравнение вида
Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0.
“акое уравнение преобразовани€ми координат приводитс€ к одному из следующих видов:
| ”равнение | ‘игура |
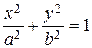
| Ёллипс |
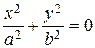
| “очка |
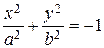
| ѕустое множество (мнимый эллипс) |
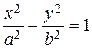
| √ипербола |
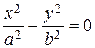
| ѕара пересекающихс€ пр€мых |
| y 2 = 2 px, p >0 | ѕарабола |
| y 2 = а 2, а ¹ 0 | ѕара параллельных пр€мых |
| y 2 = Ц а 2, а ¹ 0 | ѕустое множество (пара мнимых параллельных пр€мых) |
| y 2 = 0 | ѕр€ма€ (пара совпавших пр€мых) |
Ёллипс
Ёллипсом называетс€ множество точек плоскости, дл€ каждой из которых сумма рассто€ний до двух данных точек, называемых фокусами, есть величина посто€нна€, равна€ 2 а.
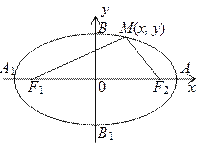 ¬ыведем уравнение эллипса. ƒл€ этого расположим координатные оси так, чтобы фокусы F 1 и F 2 располагались на оси абсцисс симметрично относительно начала координат. ѕусть рассто€ние между ними равно 2 с, значит, они имеют координаты
¬ыведем уравнение эллипса. ƒл€ этого расположим координатные оси так, чтобы фокусы F 1 и F 2 располагались на оси абсцисс симметрично относительно начала координат. ѕусть рассто€ние между ними равно 2 с, значит, они имеют координаты
F 1(Ц с, 0) и F 2(с, 0). ѕусть M (x, y) Ц произвольна€ точка эллипса. “огда из определени€ эллипса получаем уравнение
MF 1 + MF 2 = 2 a.
ѕодставл€ем MF 1 = 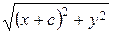 , MF 2 =
, MF 2 = 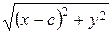 , получаем
, получаем
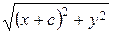 +
+ 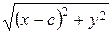 = 2 а.
= 2 а.
Ёто уравнение приводитс€ к виду
(a 2 Ц c 2) x 2 + a 2 y 2 = a 2(a 2 Ц c 2).
ѕри этом a >c, поэтому a 2 Ц c 2 > 0, и можно ввести обозначение a 2 Ц c 2 = b 2. ”равнение тогда приводитс€ к виду b 2 x 2 + a 2 y 2 = a 2 b 2. –азделив его на a 2 b 2, получим каноническое уравнение эллипса
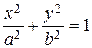 .
.
Ёллипс симметричен относительно координатных осей и пересекает ось абсцисс в точках ј 1(Ц с, 0) и ј (с, 0), ось ординат в точках B 1(Ц b, 0) и B (b, 0). Ёти четыре точки называютс€ вершинами эллипса. ќтрезок ј 1 ј называетс€ большой осью эллипса, отрезок ¬ 1 ¬ Ц малой осью. “аким образом, а и b Ц это длины большой и малой полуосей.
Ёксцентриситетом эллипса называетс€ число 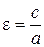 . ƒл€ любого эллипса
. ƒл€ любого эллипса 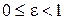 . Ёксцентриситет характеризует степень сжати€ эллипса: чем ближе эксцентриситет к 1, тем сильнее сжат эллипс. ѕри
. Ёксцентриситет характеризует степень сжати€ эллипса: чем ближе эксцентриситет к 1, тем сильнее сжат эллипс. ѕри 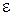 = 0 эллипс €вл€етс€ окружностью. ѕри этом фокусы эллипса сливаютс€ в одну точку, совпадающую с центром эллипса.
= 0 эллипс €вл€етс€ окружностью. ѕри этом фокусы эллипса сливаютс€ в одну точку, совпадающую с центром эллипса.
√ипербола
√иперболой называетс€ множество точек плоскости, дл€ каждой из которых разность рассто€ний до двух данных точек, называемых фокусами, есть величина посто€нна€, равна€ 2 а.
|
|
|
 ”равнение гиперболы выводитс€ аналогично уравнению эллипса из равенства
”равнение гиперболы выводитс€ аналогично уравнению эллипса из равенства
ï MF 1 Ц MF 2ï = 2 a.
«десь фокусы имеют координаты F 1(Ц с, 0) и F 2(с, 0), c > b и c 2 Ц a 2= b 2. ѕосле преобразований получаем уравнение
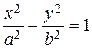 .
.
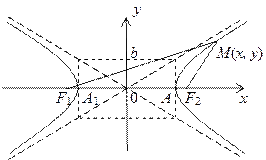
√ипербола симметрична относительно обеих координатных осей. ќна состоит из двух ветвей. √ипербола пересекает ось абсцисс в двух точках ј 1(Ц а, 0) и ј (а, 0), которые называютс€ вершинами гиперболы.
ѕр€мые  называютс€ асимптотами гиперболы. ќни могут строитьс€ с помощью четырех пр€мых, параллельных ос€м: х =
называютс€ асимптотами гиперболы. ќни могут строитьс€ с помощью четырех пр€мых, параллельных ос€м: х = 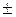 а, у =
а, у = 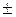 b. ¬ пересечении этих пр€мых образуетс€ пр€моугольник, который называетс€ основным пр€моугольником гиперболы.
b. ¬ пересечении этих пр€мых образуетс€ пр€моугольник, который называетс€ основным пр€моугольником гиперболы.
Ёксцентриситетом гиперболы называетс€ число 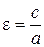 . ƒл€ любой гиперболы
. ƒл€ любой гиперболы 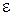 > 1. Ёксцентриситет характеризует степень сжати€ гиперболы: чем ближе эксцентриситет к 1, тем сильнее выт€нут основной пр€моугольник гиперболы.
> 1. Ёксцентриситет характеризует степень сжати€ гиперболы: чем ближе эксцентриситет к 1, тем сильнее выт€нут основной пр€моугольник гиперболы.
ѕарабола
ѕараболой называетс€ множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной пр€мой l, называемой директрисой (предполагаетс€, что фокус не лежит на директрисе).
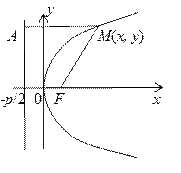 ƒл€ вывода уравнени€ параболы проведем ось абсцисс через фокус перпендикул€рно директрисе, ось ординат поместим между фокусом и директрисой на одинаковом рассто€нии от них. –ассто€ние от фокуса до директрисы обозначим через р, это число называетс€ параметром параболы. ‘окус будет иметь координаты F (p /2, 0) уравнение директрисы x = Ц p /2.
ƒл€ вывода уравнени€ параболы проведем ось абсцисс через фокус перпендикул€рно директрисе, ось ординат поместим между фокусом и директрисой на одинаковом рассто€нии от них. –ассто€ние от фокуса до директрисы обозначим через р, это число называетс€ параметром параболы. ‘окус будет иметь координаты F (p /2, 0) уравнение директрисы x = Ц p /2.
”равнение параболы выводитс€ из равенства
MF = Mј.
ѕосле преобразований получаем уравнение
y 2 = 2 px.
ѕарабола имеет ось симметрии, котора€ называетс€ осью параболы. “очка пересечени€ параболы с осью называетс€ вершиной параболы. ¬ отличие от гиперболы парабола не имеет асимптот.
¬се параболы подобны друг другу. «начит, если сжать или раст€нуть параболу в любом направлении, получим подобную параболу.






