Прямую на плоскости можно задавать уравнениями разных видов. Для решения задач следует использовать уравнение, наиболее удобное для данной задачи.
Уравнение с угловым коэффициентом:
y = kx + b. (3)
В этом уравнении угловой коэффициент k – это тангенс угла наклона прямой к оси абсцисс. Угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Недостаток этого уравнения: им невозможно задать вертикальную прямую x = a.
Общее уравнение прямой:
Ax + By + C = 0. (4)
Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности.
Уравнение прямой в отрезках:
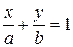. (5)
Здесь знаменатели а и b – это координаты точек пересечения прямой с соответствующими координатными осями. С помощью такого уравнения невозможно задать прямую, проходящую через начало координат или параллельную одной из осей.
Уравнение прямой, проходящей через две заданные точки M 1(x 1, y 1) и M 1(x 2, y 2):
. (6)
В этом уравнении один из знаменателей может оказаться равным 0. Тогда общее уравнение прямой получаем, приравнивая к 0 соответствующий числитель (на другую часть уравнения не обращаем внимания).
Уравнение прямой, проходящей через заданную точку M (x 0, y 0) с угловым коэффициентом k:
y – y 0 = k (x – x 0). (7)
Каноническое уравнение прямой:
. (8)
Здесь M (x 0, y 0) – точка, через которую проходит прямая, а (m, n) – направляющий вектор, задающий направление прямой.
Любой из приведенных видов уравнений легко преобразовать в любой другой.
Дополнительные формулы.
Угол между двумя прямыми.
Пусть прямые имеют угловые коэффициенты k 1 и k 2. Тогда угол j между ними определяется из условия
. (9)
Условие перпендикулярности двух прямых с угловыми коэффициентами k 1 и k 2:
k 1 k 2 = –1. (10)
Условие параллельности двух прямых с угловыми коэффициентами k 1 и k 2:
k 1 = k 2 . (11)
Расстояние от точки M (x 0, y 0) до прямой Ax + By + C = 0:
. (12)
Площадь треугольника АВС с вершинами А (x 1, y 1), В (x 2, y 2), С (x 3, y 3):
. (13)
Пример 1.4.2. Даны три точки А (3; 1), В (–2; 3), С (1; –2). а) Построить уравнение прямой АВ; б) Найти тангенс угла между прямыми АВ и АС; в) построить уравнение перпендикуляра к прямой АВ, проходящего через точку С;
г) построить уравнение прямой, параллельной АВ и проходящей через точку С; д) найти расстояние между точками А и С; е) найти расстояние между точкой С и прямой АВ; ж) найти площадь треугольника АВС.
Решение. а) Воспользуемся формулой (6):
;
;
2 x – 6 = –5 y + 5;
2 x + 5 y – 11 = 0 – общее уравнение прямой.
б) Приведем уравнение прямой АВ, полученное в пункте а) к виду (3):
.
Отсюда ее угловой коэффициент 
. Аналогично находим угловой коэффициент прямой АС, построив ее уравнение:
;
–3 x + 9 = –2 y + 2;
3 x – 2 y – 7 = 0;
;
.
Теперь по формуле (9) получаем
.
в) Угловой коэффициент k 3 перпендикуляра к АВ находим из условия (10): k 1 k 3 = –1, где из пункта б). Отсюда 
. Уравнение перпендикуляра находим по формуле (7):
y – (–2) = 
;
2 y + 4 = 5 x – 5;
5 x – 2 y – 9 = 0.
г) Согласно формуле (11), угловой коэффициент прямой, параллельной АВ, также равен . Поэтому по формуле (7) получаем уравнение
y – (–2) = 
;
5 y + 10 = –2 x + 2;
2 x + 5 y + 8 = 0.
д) Воспользуемся формулой (1):
.
е) Воспользуемся формулой (12) и уравнением прямой АВ из пункта а):
.
ж)Воспользуемся формулой (13):
.
У п р а ж н е н и я
1.5.1. Построить уравнение прямой, пересекающей координатные оси в точках (2; 0) и (0; –3).
1.5.2. Даны три точки А (–2; 1), В (1; –3), С (2; 3). а) Построить уравнение прямой АВ; б) найти тангенс угла между прямыми АВ и АС; в) построить уравнение перпендикуляра к прямой АВ, проходящего через точку С; г) построить уравнение прямой, параллельной АВ и проходящей через точку С; д) найти расстояние между точками А и В; е) найти расстояние между точкой С и прямой АВ; ж) найти площадь треугольника АВС.
Векторная геометрия
В геометрическом векторном пространстве стандартный базис состоит из векторов, имеющих единичную длину, расположенных по координатным осям и направленных в положительную сторону соответствующих координатных осей. Векторы, соответствующие осям 0 x, 0 y, 0 z, обозначают соответственно 
, 
, 
и называют основными или базовыми ортами.
Проекция вектора 
на прямую – это вектор, начало и конец которого есть проекции начала и конца вектора на эту прямую.
В разложении вектора = (a1, a2, a3) по базису: = a1 + a2 + a3 слагаемые являются проекциями вектора на соответствующие координатные оси.
Векторы, параллельные одной прямой, называются коллинеарными; параллельные одной плоскости – компланарными.
Перпендикулярные векторы называют ортогональными.
Если 
= (a, b, c) и известны координаты точки A (x 1, y 1, z 1), то координаты точки B (x 2, y 2, z 2) находим сложением этих координат: x 2 = x 1 + a, y 2 = y 1 + b, z 2 = z 1 + c. Аналогично координаты начала вектора получаются из координат конца вычитанием координат вектора.
Пример 1.6.1. Найти координаты вершины D параллелограмма ABCD, если заданы координаты А (2, –1, 1), В (4, 2, 0), С (–3, 1, –2).
Решение. Изобразим параллелограмм ABCD на рисунке (не стараясь согласовывать положение вершин с их координатами), чтобы было наглядно видно, какие векторы использовать в вычислениях. Замечаем, что
= 
= (–3 – 4, 1 – 2, –2 – 0) = (–7, –1, –2),
и получаем координаты D (2 – 7, –1 – 1, 1 – 2), или D (–5, –2, –1).
Скалярное произведение
Скалярное произведение векторов и 
определяется формулой:
= 
cosa, (1)
где a – угол между векторами и .
Свойства скалярного произведения:
1. 
= .
2. 
= 
.
3. 
= 
.
4. 
.
5. Критерий ортогональности векторов: 
.
6. Если = (a 1, a 2, a 3), 
= (b 1, b 2, b 3) то = a 1 b 1 + a 2 b 2 + a 3 b 3. Такая же формула с двумя слагаемыми для плоского случая.
Пример 1.6.2. Найти косинус угла a между векторами = (2, –1, 3), и = (3, 2, –2).
Решение. Из формулы (1) получаем cosa = 
;
= 
= –2;
;
;
cosa = 
.
Пример 1.6.3. Найти площадь треугольника АВС, если заданы координаты вершин А (2, –1, 3), В (3, 2, –2), С (0, 3, 1).
Решение. Площадь находим по формуле 
, где a – угол между АВ и АС. Вводим векторы
= (3 – 2, 2 – (–1), –2 – 3) = (1, 3, –5);
= (0 – 2, 3 – (–1), 1 – 3) = (–2, 4, –2).
cosa находим, как в примере 1.6.2:
= –2 + 12 + 10 = 20;
; 
;
cosa = 
;
;
.
Замечание. При вычислении sina сокращение не производилось специально, чтобы упростить вычисления на последнем шаге.
Векторное произведение
Упорядоченная тройка векторов , , 
пространства называется правой, если при совмещении их начал в одной точке из конца вектора поворот от к наблюдается против часовой стрелки. В противном случае тройка называется левой. Эта характеристика называется ориентацией тройки векторов.
Если векторы в тройке сдвинуть по кругу, то ориентация не изменится. Если же поменять местами два вектора, то ориентация изменится на противоположную.
Векторным произведением векторов и называется вектор = ´ такой, что:
(a) 
, где a – угол между векторами;
(b) 
, 
;
(c) векторы , , образуют правую тройку.
Свойства векторного произведения:
1. ´ = – ´ (антикоммутативность).
2. 
= 
.
3. 
= 
.
4. Критерий коллинеарности векторов: 
.
5. 
.
6. Геометрический смысл векторного произведения: площадь параллелограмма, стороны которого задаются векторами и , равна модулю их векторного произведения: 
.
7. Если = (a 1, a 2, a 3), = (b 1, b 2, b 3), причем базисные векторы образуют правую тройку, то 
.
Пример 1.6.4. Найти векторное произведение векторов = (2, –1, 3), и
= (3, 2, –2).
Решение. По свойству (7) получаем
=
= (2 – 6) – (–4 – 9) + (4 + 3) = –4 + 13 + 7 = (–4, 13, 7).
Пример 1.6.5. Найти площадь параллелограмма ABCD, если заданы координаты вершин A (3, 2, 0), C (2, –1, 2) D (1, 3, –4).
Решение. Изобразим параллелограмм ABCD на рисунке, чтобы понять, какие векторы задают стороны параллелограмма. 
Так как заданы точки A, C, D, то естественно использовать векторы 
и 
(хотя направление векторов не имеет значения, можно взять противоположные векторы):
= (3 – 1, 2 – 3, 0 + 4) = (2, –1, 4);
= (2 – 1, –1 – 3, 2 + 4) = (1, –4, 6);
= (10, –8, –7);
.
Смешанное произведение
Смешанным произведением векторов , , называется число ( ´ ) .
