| № | Дәріс тақырыбы | Оқулық және оқу құралы | Электронды оқулық және оқу құралы | ПОӘК |
| Математикалық құрылым ұғымы. Изоморфизм. Аксиомалар жүйесінің интерпретациясы жайлы түсінік | 1. Атанасян Л. С. Геометрия. М., Просвещение, ч. 1., (издания начиная с 1973) 2. Атакасяв Л. С., Гуревич Г. Б. Геометрия. М., Просвещение, 1976, ч. 1. 3. Атанасян Л. С., Атанасяя В. А. Сборник задач по геометрии. М., Просвещение, 1973,. 1. (включая все переиздания) 1. Атанасян Л. С. Геометрия. М., Просвещение, ч. 1., (издания начиная с 1973) 2. Атакасяв Л. С., Гуревич Г. Б. Геометрия. М., Просвещение, 1976, ч. І. 3. Атанасян Л. С., Атанасяя В. А. Сборник задач по геометрии. М., Просвещение, 1973,. 1. (включая все переиздания) | |||
| Аксмоималар жүйесінің қарама-қайшылықсыздығы, тәуелсіздігі және толықтығы. | ||||
| Үш өлшемді евклид кеңістігі үшін Вейль аксиомаларының қарама-қайшылықсыздығы және толықтығы. | ||||
| Түзудің, жазықтықтың, сәулені, кесіндінің, бұрыштың анықтамалары. | ||||
| Кейбір теоремаларды дәлелдеу Мектеп геометрия курсының аксиомалар жүйесі және оның Вейль аксиомаларымен байланысы | ||||
| Евклидке дейінгі геометрия. Евклид «Бастамалары». Евклид жүйесін сынау. V- постулат | ||||
| Гильберттің аксиомалар жүйесі | ||||
| Н.И. Лобачевский және оның геомтериясы. Лобачевский аксиомасы. | ||||
| Лобачевский жазықтығының геометрияның жай теоремалары. Лобачевский жазықтығының аксиомалар жүйесінің қайшылықсыздығы | 1. Атанасян Л. С. Геометрия. М., Просвещение, ч. 1., (издания начиная с 1973) 2. Атакасяв Л. С., Гуревич Г. Б. Геометрия. М., Просвещение, 1976, ч. І. 3. Атанасян Л. С., Атанасяя В. А. Сборник задач по геометрии. М., Просвещение, 1973,. 1. (включая все переиздания) | |||
| Топологиялық кеңістіктің анықтамасы. Жекеленушілік, байланыстылық, компактылық. Облыс. Үздіксіздік және гомеоморфизм. | ||||
| Топологиялық көпбейне. Мейбус жапырағы мен проективті жазықтықтың топологиялық қасиеттері. | ||||
| Беттің Эйлерлік сипаттамасы. Беттерді топологиялық жіктеу ұғымы. Көпжақтар үшін Эйлер теоремасы. | 1. Атанасян Л. С. Геометрия. М., Просвещение, ч. І., (издания начиная с 1973) 2. Атакасяв Л. С., Гуревич Г. Б. Геометрия. М., Просвещение, 1976, ч. І. 3. Атанасян Л. С., Атанасяя В. А. Сборник задач по геометрии. М., Просвещение, 1973,. 1. (включая все переиздания) | |||
| Сызық ұғымы. Жатық қисықтар. Жанама. Қисықтың ұзындығы. Иілімі және бұралымы. | ||||
| Беттің бірінші квадраттық формасы. Геодезиялық сызық ұғымы. Беттің толық иілімі. Иілімі тұрақты беттер. |
Өзін-өзі бағалауға арналған сұрақтар/тесттер/тапсырмалар/есептер/жаттығулар:
1.Абсцисса осi арқылы А(1,2) нүктесiне симметриялы нүктенi табыңдар.
A) (-1,2)
B) (1,-2)
C) (-1.-2)
D) (1,2)
E) (1,3)
2.(оху) координатттық жазықтық арқылы А(1,2,3) нүктесiне симметриялы нүктенi табыңдар.
A) (-1,-3,-2)
B) (1,3,-2)
C) (-1,3,2)
D) (-1,-3,2)
E) (1,-3,2)
3. А(1,2,3) және В(5,6,3) нүктелердiң ара қашықтығын табыңдар.
A) 2 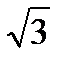
B) 4 
D) 5 
C) 6
E) 4
4.АВ кесiндiнiң орта нүктесiн табыңдар, егер А(4,1,5), В(4,-1,1) болса.
A) (-4,0,-3)
B) (4,0,3)
C) (-4,0,3)
D) (4,0,-3)
E) (0,0,3)
5. 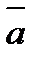 {2,0,1} және
{2,0,1} және  {-1,5,6} векторлары берiлген.
{-1,5,6} векторлары берiлген. 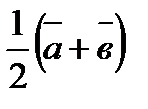 вектордың координатын табыңдар.
вектордың координатын табыңдар.
A) (-  )
)
B) ( )
)
C) (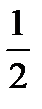 , 5,7)
, 5,7)
D) (1,5,7)
E) (-3,5,6)
6.  векторлары берiлген.
векторлары берiлген.  табыңдар
табыңдар
A) 11
B) 10
C) 12
D) 8
E) 16
7. М(1,2) нүкте арқылы өтетiн және  (3,4) векторына параллель болатын түзудiң теңдеуiн табыңдар.
(3,4) векторына параллель болатын түзудiң теңдеуiн табыңдар.
A) 4х+3у-2=0
B) 4х-3у+2==0
C) –4х-3у-2=0
D) 5х-2у+7=0
E) 6х+2у-3=0
8. С(2,3) нүктесiнен 2х+3у+7=0 түзуiне дейiнгi ара қашақтықты табыңдар.
A) 20
B) 
C) 
Д) 13
Е) 
9.А(1,2,0) нүкте арқылы өтетiн және бағыттауыш векторлары  болатын жазықтықтың теңдеуiн жазыңдар.
болатын жазықтықтың теңдеуiн жазыңдар.
A) 4х+3у+2z-2=0
B) 4x-3y-2z+2=0
C) 4x+3y-2z-2=0
D) 4x-3y+2z+2=0
E) 4x-3y-2z-2=0
10. 2x-2y+z-18=0 теңдеудi нормалдық түрге келтiру.
A) x+y-z+6=0

11. А(1,2,3) и В(2,4,6) нүктелерi арқылы өтетiн түзудiң канондық теңдеуiн жазыңдар.
А) 
В) 
С) 
Д) 
Е) 
12. 4х2+25у2-100=0 эллипстiң фокустарын табыңдар.
A) 
B) F1(21,0), F2(-21,0)
C)  , F2(21,0)
, F2(21,0)
D) F1(-21,0) 
E) F1(10,0) F2(-10,0)
13. 9х2-4у2-36=0 гиперболаның асмптоталарын табыңдар.
A) y= 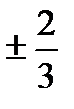 x
x
B) y= 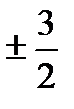 x
x
C) y=±  x
x
D) y=±x
E) y=±  x
x
14. x2+z2=2z теңдеуiмен кеңiстiктегi координаттық жүйесiнде қандай геометриялық бейне анықталады.
А)Жасаушылары (Ох) өсiне параллель болатын цилиндрлiк бет.
B) Жасаушылары (Оу) өсiне параллель болатын цилиндрлiк бет.
C) Конустық бет. D) Сфера E) Эллипсоид
15.А(1,- 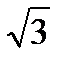 ) нүктесiнiң полярлық координаттарын табыңдар,егер координаттық жүйесiнiң бас нүктесi полюспен беттессе, ол абсцисса осi полярлық осьпен беттесе.
) нүктесiнiң полярлық координаттарын табыңдар,егер координаттық жүйесiнiң бас нүктесi полюспен беттессе, ол абсцисса осi полярлық осьпен беттесе.
A) (4,  )
)
B) (2,  )
)
C) (-2,  )
)
D) (5,  )
)
E) (2, 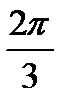 )
)
16.  векторлары берiлген.
векторлары берiлген.  векторлық көбейтiндiсiн табыңдар.
векторлық көбейтiндiсiн табыңдар.
A) (1,2,-7)
B) (-1,-2,7)
C) (1,2,7)
D) (-1,2,-7)
E) (1-2, 7)
17. А(0,0,0), В(1,2,3) C(3,4,5) D(5,-1,0) нүктелерi берiлген. АВСД тетраэдрдiң көлемiн табыңдар.
A) 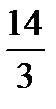
B) 
C) 
D) 
E) 
18. m қандай болғанда  түзуi және
түзуi және 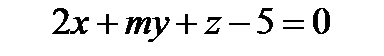 жазықтығы параллель болады?
жазықтығы параллель болады?
А)1
В)- 
С) 
Д)-1
Е)-  .
.
19.Берiлген беттi анықтаңдар.
х2+2у2-3z2+2х+4у-6z=0
А)гиерболалық цилиндр, В)Эллипсоид.
С)екiншi реттi конус, Д) сфера.
Е)гиперболалақ параболойд,
21. ордината осi арқылы В(1,2) нүктесiне симметриялы нүктенi табыңдар. A) (-1,-2)
B) (-1,2)
C) (1,2)
D) (2,1)
E)(-2,1)
22.(охz) координаттық жазықтықтық арқылы В(1,2,3) нүктесiне симметриялы нүктенi табыңдар.
A) (-1,-2,-3)
B) (1,-2,3)
C) (-1,-2,3)
D) (1,-2,-3)
E) (-1,2,-3)
23.А(1,2,3) және В(3,2,4) нүктелердiң ара қашықтығын табыңдар.
A) 
B) 
C) 
D) 6
E) 5
24. АВ кесiндiнiң орта нүктесiн табыңдар, егер А(2,3,1), В(-2,1,3) болса.
A) (0,-2,-2)
B) (0,2,2)
C) (0,2,-2)
D) (0,-2,2)
E) (2,0,2)
25. а (5,0,6) және в (1,3,3) векторлары берiлген. 1/3(а+в) векторының координаттарын табыңдар.
A) (-2,-1,3)
B) (2,1,3)
C) (-2,1,-3)
D) (-2,1,3)
E) (-2,-1,-3)
26. а (5,0,-2) и в (1,7/2,-3) векторлары берiлген. а·в табыңдар.
A) 12
B) 11
C) 10
D) 29/2
E) 7/2
27. А(2,3) нүкте арқылы өтетiн және а (1,5) векторына перпендикуляр болатын түзудiң теңдеуiн табыңдар.
A) x-5y+17=0
B) x+5y-17=0
C) x-5y-17=0
D) x+2y-6=0
E) x-2y+3=0
28. В(5,6) нүктесiнен 4х+3у-2=0 түзуiне дейiнгi ара қашықтықты табыңдар. A) 8
B) 36/5
C) 5/36
D) 10
E) 7
29.А(1,0,0), С(0,0,3) нүктелерi арқылы өтетiн жазықтықтың теңдеуiн жазыңдар.
A) 6x-3y-2z-6=0
B) 6x+3y+2z-6=0
C) 6x-3y+2z+6=0
D) 6x+3y-2z+6=0
E) 6x-3y-2z+6=0
30. m қандай болғанда 2х+3у-z+2=0 және m x-6y+2+7=0 жазықтықтар параллель болады.
A) 4
B) -4
C) 3
D) -3
E) 5
31. А(1,-1,-3) нүктесi арқылы өтетiн және (x-1)/2=(y+2)/4=(z-1)/3 түзуiне параллель болатын түзудiң параметрлiк теңдеуiн жазыңдар.
A) x=2t-1, y=4t-1, z=3t-3
B) x=2t+1, y=4t-1, z=3t-3
C) x=2t-1, y=4t-1, z=3t+3
D) x=2t+1, y=4t+1, z=3t+3
E) x=2t-1, y=4t+1, z=3t+3
32. Берiлген сфераның центрiн және радиусын табыңдар
x²+y²+z²-12x+4y-6z=0
A) (-6,2,3), R=6
B) (6,-2,3), R=7
C) (-6,2,-3), R=7
D) (6,-2,-3), R=6
E) (-6,2,-3), R=7 
33. а {2,3,4,} және в {1,2,1} векторлары берiлген.[ а·в ] векторлық көбейтiндiнi табыңдар.
A) (5,2,1)
B) (-5,2,1)
C) (5,-2,1)
D) (-5,-2,1)
E) (–5,-2,-1)
34. А(0,0,0), В(1,2,3), С(3,4,5) и D(5,-1,0) нүктелерi берiлген AB, AC, AD векторлармен құралған паралелепипедтiң көлемiн табыңдар.
А)18
B) 14
C) 16
D) 10
E) 14/3
35. 2х2-4у-z2=0 екiншi реттi беттi анықтаңдар.
А)Элипстiк параболоид, В) бiр қуысты гиперболоид С) сфера
Д)Элипсоид
Е) қос қуысты гиперболоид.
36. Жазықтықтың бағытын өзгетпейтiн бiрiншi реттi қозғалыс:
А) осьтiк симметрия. В) центрлiк симметрия..
С) сырғанау симметрия. Д) инверсия.
Е) гомотетия.
37. Ордината осi арқылы С (2,3) нүктесiне симметриялы нүктенi тыбыңдар.
A) (-2,-3)
B) (-2,3)
C) (-3,2)
D) (3,-2)
E) (-3,-2)
38. (Oyz) координаттық жазықтық арқылы С (1,2,3) нүктесiне симметриялы нүктенi табыңдар.
A)(- 1, - 2, -3)
B) (- 1, 2, 3)
C) (- 1, - 2, 3)
D)(1, 2, - 3)
E)(1, -2, 3)
39. А(1,2,3) және В(1,5,4) нүктелердiң ара қашықтығын табыңдар.
А) 
В) 
С) 10
Д) 5
Е) 2 
40. АВ кесiндiнiң орта нүктесiн табыңдар, егер А(1,2,3), В(4,2,1) болса.
А)(-  , 2, 2)
, 2, 2)
В) ( , 2,2)
, 2,2)
С) (-  , -2, -2)
, -2, -2)
Д) (5,  , 2)
, 2)
Е) (5, 2,  )
)
41.  векторлары берiлген.
векторлары берiлген.  вектордың координаттарын табыңдар.
вектордың координаттарын табыңдар.
А) (2,0, -  )
)
В) (2,0,  )
)
С) (-2,0,  )
)
Д) (-2,0, -  )
)
Е)(2,0,2)
42. 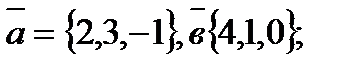 векторлары берiлген.
векторлары берiлген.  табыңдар.
табыңдар.
А)12;
В)11;
С)10;
Д)9;
Е)8.
43. А(1,2) және В(5,3) нүктелерi арқылы өтетiн түзудiң теңдеуiн жазыңдар
А) х+4у-7=0;
В) х-4у+7=0;
С) х-4у-7=0;
Д) 2х-3у+7=0;
Е) 5х+3у-3=0;
44. А(2,1) нүкесiнен 4х+3у-1=0 түзуiне дейiнге ара қашықтықты табыңдар.
А)3;
В)2;
С)4;
Д)  ;
;
Е)  .
.
45. А(1,2,3), В(-1,2,4), С(0,2,5) нүктелер арқылы өтетiн жазықтықтың теңдеуiн жазыңдар.
А) х-2=0;
В) у-2=0;
С) 2х+3у-1=0;
Д)2х-3у+1=0;
Е)у+2=0.
46.m қандай болғанда 3х-5у+mz-3=0 және х+3у+2z+5=0 жазықтықтар перпендикуляр болады?
А)7;
В)6;
С)4;
Д)5;
Е)8.
47. С (2,3,1) нүктесi арқылы өтетiн және 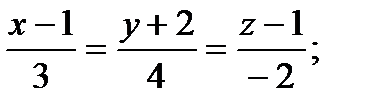 түзуiне параллель болатын түзудiң канондық теңдеуiн жазыңдар.
түзуiне параллель болатын түзудiң канондық теңдеуiн жазыңдар.
А) 
В) 
С) 
Д)  ;
;
Е) 
48. 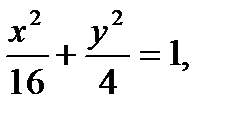 эллипсқа тиiстi және ординатасы
эллипсқа тиiстi және ординатасы  болатын нүктелердi табыңдар.
болатын нүктелердi табыңдар.
А) 
В) 
С) 
Д) 
Е) 
49.  гиперболаға К(10,4) нүктесiнде жанаманы жүргiзiңдер.
гиперболаға К(10,4) нүктесiнде жанаманы жүргiзiңдер.
А) х+2у+2=0
В) х-2у-2=0
С) х-2у+2=0
Д) х+2у-2=0
Е) х-2у-1=0
50.Берiлген екiншi реттi сызықтың түрiн анықтаңдар. х2+у2-2х+6у+9=0
А)эллипс
В)парабола
С)гипербола
Д)шеңбер
Е)қилысатын қос түзулер.
51. Параллель көшiруде А(2,1,-1) нүктесi А1 (1,-1,0) нүктесiне ауысады.Координат жүйесiнiң бас нүктесi қандай нүктеге ауысады?
А)(-1,-2,1)
В) (1,2,-1)
С) (-1,2,-1)
Д) (1,-2,1)
Е) (1,2,1)
52. а(1,2,3) және в(3,1,2) векторлардың векторлық көбейтiндiсiн табыңдар.
А)(-1,7,5)
В) (1,7,-5)
С) (-1,-7,-5)
Д) (1,-7,5)
Е) (1,7,5)
53. АВ(1,2,3), АС(3,4,5) және АД(5,-1,0) векторлары берiлген. Осы векторлармен құралған параллелепипедтiң көлемiн табыңдар.
Даны векторы  .
.
А)16
В)14
С)18
Д) 
Е) 
54. к қандай болғанда келесi түзулер

перпендикуляр болады.
А)6.
В)7.
С)-4.
Д)5.
Е)3.
55. Берiлген екiншi реттi беттiң түрiн анықтаңдар.
4х2+4у2-z2-16у+20=0
А) эллипстiк параболоид В) бiр қуысты гиперболоид
С) қос қуысты гиперболоид Д) сфера
Е)эллипсоид
56. Жазықтықтың қозғалысы
А) ауданды сақтамайды
В) ара кашықтықты сақтайды
С) коллинеар үш нүктенi үш коллинеар емес нүктеге ауыстырады
Д) түзу сызықты нүктелер қатарын түзулер шоғырына ауыстырады
Е) параллель түзулердi қиылысатын тузулерге ауыстырады
57. Абсцисса осi арқылы Д(2,3) нүктесiне симметриялы нүктенi табыңдар. A) (-2,-3)
B) (2,-3)
C) (3,2)
D) (-3,-2)
E) (-3,2)
58. (Оху) координаттық жазықтық арқылы Д(1,2,3) нүктесiне симметриялы нүктенi табыңдар.
A) (-1,-2,-3)
B) (1,2,-3)
C) (-1,-2,3)
D) (-1,2,-3)
E) (1,-2,3)
59. А(1,2,3) и В(6,2,4) нүктелердiң ара қашықтығын табыңдар,
А) 

D) 
E) 26
60. АВ кесiндiсiнiң орта нүктесiн табыңдар, егер А(4,1,5), В(4,-1,1) болса.
A) (2,-3,7)
B) (2,3,  )
)
C) (2,3, -  )
)
D) (-2,-3,7)
E) (2,3,7).
61.  (4,6,-2),
(4,6,-2),  (3,-6,5) векторлары берiлген,
(3,-6,5) векторлары берiлген,  вектордың координаттарын табыңдар.
вектордың координаттарын табыңдар.
A) (- 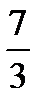 ,0,-1)
,0,-1)
B) (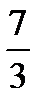 ,0,1)
,0,1)
C) (- 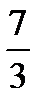 ,0,1)
,0,1)
D) (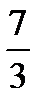 ,0,-1)
,0,-1)
E) (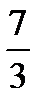 ,0,
,0,  )
)
62.  {1,2,3}и
{1,2,3}и  (5,6,7) векторлары берiлген.
(5,6,7) векторлары берiлген. 
 табыңдар.
табыңдар.
A) 36
B) 38
C) 30
D) 0
E) 40
63. Ох осiмен 450 құратын және А(1,2) нүктесi арқылы өтетiн түзудiң теңдеуiн табыңдар.
A) х+у-1=0
B) х - у+1=0
C) х+у+1=0
D) 3х-2у+5=0
E)  +у-7=0
+у-7=0
64.А(3,-2) нүктесiнен 3х+4у-5=0 түзуiне дейiнгi ара қашықтықты табыңдар.
A) 
В)0,8
C) 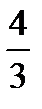
D) 5
E)-0,8
65. С(1,2,3) нүкте арқылы өтетiн нормалдық векторы  (2,1,4) болатын жазықтықтың теңдеуiн жазыңдар.
(2,1,4) болатын жазықтықтың теңдеуiн жазыңдар.
A) 2х-у-4z+16=0
B) 2х+у+4z-16=0
C) 2х+у-4z+16=0
D) 2х-у+4z+16=0
E) 2х+у+4z+16=0
66. х+2у-3z-6=0 жазықтықтың теңдеуін «кесiнделер» түрiнде жазыңдар.
А)  ;
;
В) 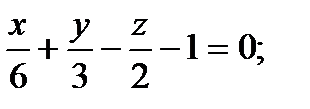
С)  ;
;
Д) 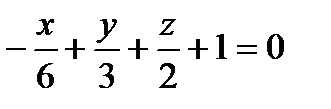 ;
;
Е) 
67. А (1,2,3) нүктесi арқылы өтетiн және  (3,2,4) векторына параллель болатын түзудiң канондық теңдеуiн жазыңдар.
(3,2,4) векторына параллель болатын түзудiң канондық теңдеуiн жазыңдар.
А) 
В) 
С) 
Д) 
Е) 
68.  эллипске тиiстi және ординатасы
эллипске тиiстi және ординатасы  болатын нүктелердi табыңдар.
болатын нүктелердi табыңдар.
А) 
В) 
С) 
Д) 
Е) 
69. у2=8х параболға К(2,4) нүктесiнде жанаманы жүргiзiең.
А)2х+у-4=0
В)2х-у-4=0
С)2х-у+4=0
Д)2 х+у +4=0
Е) y+2х -3 =0
70. х2+у2-2х+6у+9=0 екiншi реттi сызықтың түрiн анықтаңдар.
А) гипербола
В) шеңбер
С) парабола
Д) эллипс
Е) қиылысатын қос түзулер
71. К(3,  ) нүктесiнiң декарттық тiкбұрышты координаттарын табыңдар, егер полюс координатық жүесiнiң бас нүктесiмен беттессе, ал полярлық осi абсцисса осiмен беттессе. А)(
) нүктесiнiң декарттық тiкбұрышты координаттарын табыңдар, егер полюс координатық жүесiнiң бас нүктесiмен беттессе, ал полярлық осi абсцисса осiмен беттессе. А)( )
)
В)( )
)
С)( )
)
Д)( )
)
Е)( )
)
72.  векторлары берiлген.
векторлары берiлген.  табыңдар.
табыңдар.
А) 3 
В) 5 
С) 10
Д) 5
Е) 15
73. А(1,2,3), В(3,2,0), С(4,5,6),Д(0,0,1) нүктелерi берiлген. АВСД тетраэдрдiң көлемiн табыңдар.
А) 

В) 
С) 
Д) 
Е)7
74. К(2,-3,-5) нүктесi арқылы өтетiн және 6х-3у-5z+2=0 жазықтығына перпендикуляр болатын түзудiң теңдеуiн жазыңдар.
А) 
В) 
С) 
Д) 
Е) 
75. Берiлген екiншi реттi беттiң түрiн жазыңдар: х2+2у2-3z2+2х+4у+6z=0
А)конус
В)бір қуысты гиперболоид
С)гиперболалық параболоид
Д)сфера
Е)эллипсоид
76.Аффиндiк түрлендiруде
А)түзу шеңберге ауысады,
В)түзу түзуге ауысады, С)параллель түзулер қилысатын түзулерге ауысады,
Д)трапеция квадратқа ауысады, Е) трапеция параллелограмға көшедi.
77.К (3,  ) нүктесiнiң декарттық тiкбұрышты координаттарын табыңдар, егер полюс координатық жүйесiнiң бас нүктесiмен беттессе, ал полярлық осi абцисса осiмен беттессе.
) нүктесiнiң декарттық тiкбұрышты координаттарын табыңдар, егер полюс координатық жүйесiнiң бас нүктесiмен беттессе, ал полярлық осi абцисса осiмен беттессе.
А)  В)
В)  С)
С) 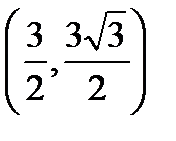 Д) (3,-4) Е)
Д) (3,-4) Е) 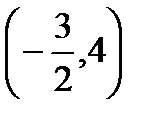
78.Р(2,3) нүкте арқылы өтетiн және b(3,-5) векторға параллель болатын түзудiң параметрлiк теңдеуiн жазыңдар.
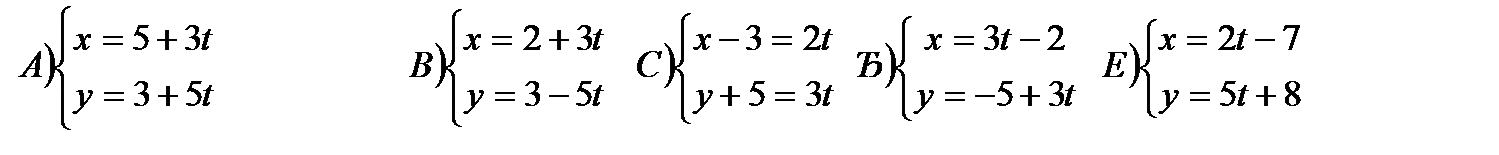
79. Түзу параметрлiк түрiнде берiлген:  .Оның бағыттауыш векторын табыңдар.
.Оның бағыттауыш векторын табыңдар.
А)  В) (3,-1) С) (6,2) Д) (5,0) Е) (7,-4)
В) (3,-1) С) (6,2) Д) (5,0) Е) (7,-4)
80. А(0,2), В(3,1), С(-1,4), Д(-5,8), Е(11,5) нүктелерi берiлген. Олардың кайсысы х=-1+t, y=4-2t түзуге тиiстi.
А) Е,Д В) А,С С) Е,В Д) Д,Е Е) Е
81. Берiлген түзудiң 11х-5у-3=0 теңдеуiн нормалдық түрге келтiрiңдер.

 .
.
82.  теңдеудi нормалдық түрге келтiрiңдер.
теңдеудi нормалдық түрге келтiрiңдер. 

83. Н(2,1,-1) нүкте арқылы өтетiн және нормаль векторы  болатын жазықтықтың теңдеуiн жазыңдар.
болатын жазықтықтың теңдеуiн жазыңдар.
А) 2х-у-z-7=0 В) х-2у+3z+3=0 С)3х-у—2z+5у=0
Д) 3х+у-2z=0 Е) 2х+5у+7z=0
84. Координат жүйесiнiң бас нүктесi арқылы өтетiн және нормаль векторы  болатын жазықтықтың теңдеуiн жазыңдар.
болатын жазықтықтың теңдеуiн жазыңдар.
А) 5х-3у=0 В)5х-3z=0 C)5z-3x=0 Д)2х-8у+z=0 E)3x-2y-5z=0
85. Жазықтықтың теңдеуi берiлген: x+2y-3z-6=0. Оның «кесiндiлер» түрiндегi теңдеуiн жазыңдар.


86. 3у-z=0 және 2у+z=0 жазықтықтардың арасындағы бұрышты табыңдар.
А) 300 В) 450 С) 1500 Д) 600 Е) 900
87. l қандай болғанда 2х+3у+3z-5=0 және lx-6y-6z+2=0 жазықтықтар параллель болады. А) 5 В) -4 С) 7 Д) 2 Е) -3
88. l қандай болғанда 3x-5y+lz-3=0 және x+3y+2z+5=0 жазықтықтар перпендикуляр болады?
А) 7 В)6 С) 4 Д) 5 Е) 8
89. А(3,-1,2),В(4,-1,-1),С(2,0,2) нүктелер арқылы өтетiн жазықтықтың теңдеуiн жазыңдар.
А) 2х-у+3z-5=0 B)3x+3y+z-8=0 C)x+4y-z+6=0 Д)x-5y=0
E)4y-z=0
90. 2x-2y+z-18=0 жазықтықтың теңдеуiн нормалдық түрге келтiрiңдер. 

91. К(3,-6,7) нүктесiнен 4х-3у-1=0 жазықтығына дейiнгi ара кашықтықты табыңдар
А) 3 В) 2 С) 5 Д) 2,5 Е) 1,6
92. Координат жүйесiнiң бас нүктесi арқылы өтетiн және 4х-у+3z-1=0, x+5y-z+2=0 жазықтықтардың қиылысуы арқылы өтетiн жазықтықтың теңдеуiн жазыңдар.
А) 6х-у-z+5=0 В)9х+3у+5z=0 С)9х+у+5z-6=0
Д)7х+2у+5z-3=0 Е)4у-z-5=0
93. М(2,0-3) нүктесi арқылы өтетiн және  векторына параллель болатын түзудiң канондық теңдеуiн жазыңдар.
векторына параллель болатын түзудiң канондық теңдеуiн жазыңдар.


94. Берiлген М (1,2,-4) және Н (-1,3,-5) нүктелерi арқылы өтетiн түзудiң канондық теңдеуiн жазыңдар. 

95. Берiлген М (1,-1,-3) нүкте арқылы өтетiн және берiлген
 түзуiне параллель болатын түзудiң параметрлiк
түзуiне параллель болатын түзудiң параметрлiк
теңдеуiн жазыңдар.

96. Берiлген  және
және  түзулердiң арасындағы сүйiр бұрышты табыңдар.
түзулердiң арасындағы сүйiр бұрышты табыңдар.

97. k қандай болғанда  және x=6t, y=-4t-1, z=2t+1 түзулерi параллель болады?
және x=6t, y=-4t-1, z=2t+1 түзулерi параллель болады?
А)2 В) 1 С) -5 Д) 0,6 Е) -2
98. к қандай болғанда 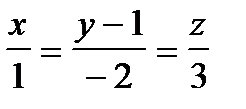 және
және 
түзулерi перпендикуляр болады?
А) 6 В) 7 С) -4 Д) -3 Е) 5
99. x=1+11t, y=2-7t, z=5-8t түзудiң және 7x-8y+2z-10=0
жазықтықтың арасындағы бұрышты табыңдар.

100. с қандай болғанда x=-1+3t, y=2+сt, z=-3-2t түзу және
x+3y+3z-2=0 жазықтық қиылыспайды?
А) 2 В) 1 С) -6 Д) 0,4 Е) -0,5
101. а және с қандай болғанда  түзу аx+8y+сz+2=0
түзу аx+8y+сz+2=0
жазықтығына перпендикуляр болады?
А) а=2,с=4 В) а=5, с=1 С)а=-5, с=-4 Д)а=1, с=-2 Е)а=0,5 с=4
102. а және с қандай болғанда  түзу
түзу
аx+y-2z+с=0 жазықтығына тиiстi болады?
А) а=3,с=6 В) а=-2, с=11 С)а=-7, с=8 Д)а=9, с=12 Е)а=-5, с=-8
103. А (2,-3,-5) нүкте арқылы өтетiн және 6x-3y-5z+2=0
жазықтығына перпендикуляр болатын түзудiң теңдеуiн
жазыңдар.


104. В(1,-1,2) нүкте арқылы өтетiн және х+у-z+7=0 жазықтығына параллель болатын жазықтықтың теңдеуiн жазыңдар.
А) x-y-z-2=0 B) x+y-z+2=0 C) x-y+z-1=0
Д) x-y-z+9=0 Е) x-y-z-1=0
105. С(1,-1,-1) нүкте арқылы өтетiн және  түзуiне перпендикуляр болатын жазықтықтың теңдеуiн жазыңдар.
түзуiне перпендикуляр болатын жазықтықтың теңдеуiн жазыңдар.
А) 3x-2y-4z+1=0 B) 2x-3y+4z-1=0 C) 4x+y-2z-5=0
Д) x-y+6=0 Е) 2x-y+9z-2=0
106. х=2t+1, y=-3t+2, z=2t-3 түзу арқылы және К(2,-2,1) нүктесi
арқылы өтетiн жазықтықтың теңдеуiн жазыңдар.
А) 4xy+5z-3=0 B) 4x+6y+5z-1=0 C) 2x-2y-z-10=0
Д) x-4y-z+5=0 Е) x-y+z-4=0
107. Оz осi арқылы өтетiн және x=2+t, y=2t, z=1+3t түзуiне параллель болатын жазықтықтың теңдеуiн жазыңдар.
А) 3x-y=0 B) 2x-y=0 C) x-3y-5=0
Д) 2x-2y+2=0 Е)6x-5y-6=0
108. Берiлген  түзу арқылы өтетiн және
түзу арқылы өтетiн және
3x+2y-z-5=0 жазықтығына перпендикуляр болатын
жазықтықтың теңдеуiн жазыңдар.
А) x-y-3z-9=0 B) x-8y-13z+9=0 C) x-y=0
Д) 3x-4y=0 Е) -4x-y+z-7=0
109. Р(1,-1,-2) нүктесiнен келесi  түзуге дейiнгi
түзуге дейiнгi
ара кашықтықты табыңдар.
А) 5 В) 7 С) 6 Д) 2 Е) 1
110.Берiлген  және
және 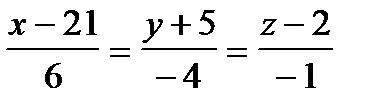 түзулердiң ара
түзулердiң ара
кашықтықтарын табыңдар.
А) 7 В) 17 С) 2 Д) 13 Е) 8
111. Берiлген  және
және  нүктелерiне дейiнгi ара кашықтықтарының қосындысы 16 болатын нүктелер жиынын анықтаңдар.
нүктелерiне дейiнгi ара кашықтықтарының қосындысы 16 болатын нүктелер жиынын анықтаңдар.
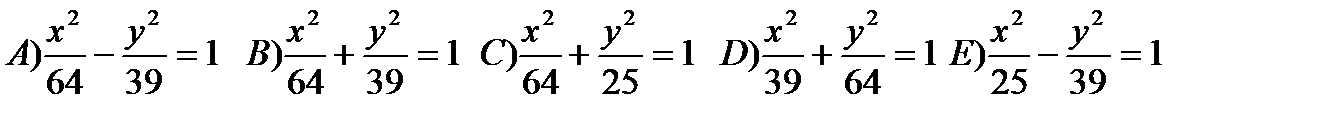
112.  эллипстiң фокустарын табыңдар.
эллипстiң фокустарын табыңдар.


113. Төбелерiнiң ара кашықтығы 8, ал фокустарының ара кашықтығы 10 болатын гиперболаның канондық теңдеуiн табыңдар.
 78. 114. Директрисасының теңдеуi х-20=0 болатын параболаның
78. 114. Директрисасының теңдеуi х-20=0 болатын параболаның
канондық теңдеуiн табыңдар.
 115.Екiншi реттi сызық
115.Екiншi реттi сызық  теңдеумен берiлген. Оның
теңдеумен берiлген. Оның 
эксцентриситетiн табыңдар.

116. Эллипс берiлген 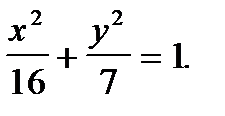 Үлкен осiнiң екі шетiнен директрисасының бiреуiне дейiнгi ара кашықтықтарды табыңдар.
Үлкен осiнiң екі шетiнен директрисасының бiреуiне дейiнгi ара кашықтықтарды табыңдар.

117. l қандай болғанда 2х+3у+3z-5=0 және lx-6y-6z+2=0
жазықтықтар параллель болады?
А) 5 В) -4 С) 7 Д) 2 Е) -3






