Умозаключение – это способ получения нового знания на основе некоторого имеющегося.
Умозаключение состоит из посылок и заключения. Посылки – это высказывания, содержащие исходное знание. Заключение – это высказывание, содержащее новое знание, полученное из исходного. Как правило, заключение отделяется от посылок с помощью слов «следовательно», «значит».
Дедуктивным называется умозаключение, в котором посылки и заключение находятся в отношении логического следования.
Дедуктивные умозаключения иначе называют правильными. В правильном умозаключении истинность посылок гарантирует истинность заключения. Наиболее часто встречаются следующие формы правильных умозаключений:
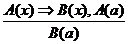 (правило заключения);
(правило заключения);
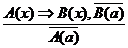 (правило отрицания);
(правило отрицания);
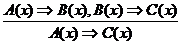 (правило силлогизма).
(правило силлогизма).
Неполная индукция – это умозаключение, в котором на основании того, что некоторые объекты класса обладают данным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.
Под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.
П р и м е р 1. Проверьте, правильны ли следующие умозаключения:
а) Если четырехугольник – прямоугольник, то его диагонали равны. ABCD – прямоугольник. Следовательно, его диагонали равны.
б) Если число делится на 6, то оно делится на 3. Число 24 делится на 3, значит, число 24 делится на 6.
в) Если четырехугольник ромб, то он параллелограмм. Диагональ параллелограмма делит его на два равных треугольника. Следовательно, диагональ ромба делит его на два равных треугольника.
Р е ш е н и е. а) Для решения вопроса о правильности умозаключения выявим его логическую форму, для чего введем следующие обозначения. Пусть А(х) – «четырехугольник х – прямоугольник», а В(х) – «диагонали четырехугольника х равны». Тогда первую посылку можно записать в виде: А(х) ⇒ В(х), вторую – А(a), а заключение – В(а) (прямоугольник ABCD обозначен в виде элемента а). Таким образом, форма данного умозаключения такова: 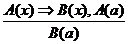 . Оно построено по правилу заключения. Следовательно, данное умозаключение правильное.
. Оно построено по правилу заключения. Следовательно, данное умозаключение правильное.
б) Сформулируем предложение «Если число делится на 6, то оно делится на 3» в виде импликации двух предикатов А(х) ⇒ В(х), где А(х) – «Число х делится на 6», В(х) – «Число х делится на 3». Эта импликация представляет собой логическое следование, так как множество чисел, делящихся на 6, является подмножеством чисел, делящихся на 3. Посылка «Число 24 делится на 3» является высказыванием, в которое превращается предикат В(х) при х = 24, т. е. это В(24). Заключение рассуждения представляет собой высказывание А(24).
Форма данного умозаключения такова: 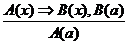 . Форма не является правильной. И хотя заключение получилось истинным (24 делится на 6), при другом значении х, например при х = 21, получим ложный вывод. Таким образом, данное умозаключение не является правильным.
. Форма не является правильной. И хотя заключение получилось истинным (24 делится на 6), при другом значении х, например при х = 21, получим ложный вывод. Таким образом, данное умозаключение не является правильным.
в) Введем обозначения: А(х) – «Четырехугольник х – ромб», В(х) – «Четырехугольник х – параллелограмм», С(х) – «Диагональ четырехугольника х делит его на два равных треугольника». Тогда первую посылку можно записать в виде: А(х) ⇒ В(х), вторую – В(х) ⇒С(х), а заключение – А(х) ⇒С(х). Форма данного умозаключения является правильной и представляет собой правило силлогизма: 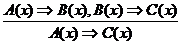 .
.
^
Задания для самостоятельной работы по теме 6:
1  . В каждом из следующих умозаключений выделите посылки и заключение, проверьте правильность умозаключений с помощью кругов Эйлера: а) Все учащиеся нашего класса в каникулы ходили в театр. Петя не был в театре в дни каникул. Следовательно, Петя – учащийся не нашего класса. б) Все деревья – растения. Сосна – дерево. Значит, сосна – растение. в) Каждый учащийся нашего класса занимается в каком-то кружке. Петя занимается в кружке по рисованию. Следовательно, Петя учится в нашем классе. г) Все антилопы стройные. Стройные животные радуют глаз. Все антилопы радуют глаз.
. В каждом из следующих умозаключений выделите посылки и заключение, проверьте правильность умозаключений с помощью кругов Эйлера: а) Все учащиеся нашего класса в каникулы ходили в театр. Петя не был в театре в дни каникул. Следовательно, Петя – учащийся не нашего класса. б) Все деревья – растения. Сосна – дерево. Значит, сосна – растение. в) Каждый учащийся нашего класса занимается в каком-то кружке. Петя занимается в кружке по рисованию. Следовательно, Петя учится в нашем классе. г) Все антилопы стройные. Стройные животные радуют глаз. Все антилопы радуют глаз.
 А)
А)
Б  )
)



2. Выделите логическую форму умозаключений, приведенных в № 1, и укажите те из них, которые построены по правилу:
а) отрицания;
б) заключения;
в) силлогизма.
3. Сделайте выводы из каждой пары посылок, если это возможно.
а) Некоторые деревья зеленые и летом и зимой. Береза – дерево.
б) Мальчики и девочки второго класса пойдут гулять. Галя – ученица этого класса.
в) Все, кто имеет пятерки по математике, будут участвовать в олимпиаде. Лена имеет пятерки по математике и по русскому языку.
г) Все, кто имеет пятерки по математике, будут участвовать в олимпиаде. Лена имеет пятерки по математике или по русскому языку.






