Способы задания множеств.
Понятие множества является неопределяемым понятием. Его смысл разъясняется на примерах. Можно говорить о множестве жителей города Саратова, о множестве домов на конкретной улице, о множестве букв в слове «командир», о множестве натуральных чисел, меньших 20 и т. д.
Множества принято обозначать большими латинскими буквами, например, А, В, С, …, Х, Y, Z. Объекты, из которых состоит множество, называются его элементами. Их принято обозначать маленькими латинскими буквами: a, b, c, d. Если множество А состоит из элементов a, c, k, то записывают это так: А = { a, c, k }.
Проказница-Мартышка,
Осел,
Козел
Да косолапый Мишка
Затеяли сыграть Квартет.
Достали нот, баса, альта, две скрипки
И сели на лужок под липки, -
Пленять своим искусством свет.
Ударили в смычки, дерут, а толку нет.
"Стой, братцы, стой! — кричит Мартышка. -
Погодите!
Как музыке идти? Ведь вы не так сидите.
Ты с басом, Мишенька, садись против альта,
Я, прима, сяду против вторы;
Тогда пойдет уж музыка не та:
У нас запляшут лес и горы!"
Расселись, начали Квартет;
Он все-таки на лад нейдет.
"Постойте ж, я сыскал секрет? -
Кричит Осел, — мы, верно, уж поладим,
Коль рядом сядем".
Послушались Осла: уселись чинно в ряд;
А все-таки Квартет нейдет на лад.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть.
Случилось Соловью на шум их прилететь.
Тут с просьбой все к нему, чтоб их решить сомненье.
"Пожалуй, — говорят, — возьми на час терпенье,
Чтобы Квартет в порядок наш привесть:
И ноты есть у нас, и инструменты есть,
Скажи лишь, как нам сесть!" -
"Чтоб музыкантом быть, так надобно уменье
И уши ваших понежней, -
Им отвечает Соловей, -
А вы, друзья, как ни садитесь;
Всё в музыканты не годитесь".
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø.
Множество может быть задано перечислением всех его элементов или описанием характеристического свойства его элементов. Характеристическим свойством называется такое свойство, которым обладают все элементы данного множества и не обладают никакие другие объекты. Например, запись А = { х | х – житель Саратова } означает, что множество А состоит из жителей Саратова.
Множества, состоящие из чисел, называют числовыми множествами.
N – множество натуральных чисел,
Z – множество целых чисел,
N о или Z о – множество целых неотрицательных чисел,
Q – множество рациональных чисел,
R – множество действительных чисел.
Задания для самостоятельной работы по теме 1:
Назовите и запишите множество зверей из басни
И.А. Крылова «Квартет», используя способ:
а) перечисления элементов;
б) задания характеристического свойства.
Принадлежит ли Соловей этому множеству?
Приведите примеры множеств, элементами которых являются:
а)неодушевленные предметы,
б)геометрические фигуры,
в)животные,
г)растения.
Задайте множество с помощью перечисленных элементов:
X={x/x 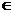 N, 0
N, 0  x
x  4}
4}
X={x/x 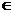 N, -2
N, -2  x
x  6}
6}
X={x/x 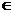 Z, -3
Z, -3  x
x  5}
5}
X={x/x 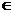 Z, 0
Z, 0  x
x  4}
4}
В данном множестве все элементы, кроме одного, обладают некоторым свойством. Опишите это свойство и найдите элемент, не обладающий им: а) { треугольник, квадрат, трапеция, круг, правильный шестиугольник }; б) { лев, лисица, гиена, слон, рысь }; в) { бежать, смотреть, синий, знать, читать }; г) {2, 6, 15, 84, 156}; д) {1, 9, 67, 81, 121}.
Лекция 2. Отношения между множествами. Операции над множествами. Разбиение множества на классы.
Между двумя множествами существует пять видов отношений. Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В =∅. Например, А = { a, c, k }, В = { d, e, m, n }, общих элементов у этих множеств нет, поэтому множества не пересекаются.
Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠∅. Например, множества А = { a, c, k } и В = { c, k, m, n } пересекаются, т. к. у них есть общие элементы c, k.
Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В⊂ А)
Пустое множество и само множество называют несобственными подмножествами. Остальные подмножества множества А называются собственными. Для каждого множества, состоящего из n элементов можно образовать 2 n подмножеств. Если рассматривают лишь подмножества некоторого множества U, то U называют универсальным множеством.
Если множества А и В состоят из одних и тех же элементов, то они называются равными.
Например, А = { a, c, k, m, n } и В = { m, n, a, c, k }, А = В.
Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.

а) б) в) г) д)
Определение. Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А∩ В. Таким образом, по определению,
А ∩ В = { х | х ∈ А и х ∈ В}.
Например, если А = { a, c, k, m, n } и В = { a, b, c, d, e }, то А ∩ В = { a, c }.
Если изобразить множества А и В при помощи кругов Эйлера-Венна, то пересечением данных множеств является заштрихованная область (рис. 3).
Для пересечения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∩ В = В ∩ А.
2) Сочетательное или ассоциативное свойство:(А ∩ В) ∩ С = А ∩ (В ∩ С).
3) А ∩ ∅ = ∅ (пустое множество является поглощающим элементом).
4) А ∩ U = А (универсальное множество является нейтральным элементом).
5) Если В ⊂А, то А∩В = В
Определение. Объединением множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А или множеству В.

Объединение множеств А и В обозначают А∪ В. Таким образом, по определению, А ∪ В = { х | х ∈А или х ∈В}. Например, если А = { a, c, k, m, n } и В = { a, b, c, d, e }, то А ∪ В = { a, c, k, m, n, b, d, e }.
Если изобразить А и В при помощи кругов Эйлера-Венна, то объединением данных множеств является заштрихованная область (рис. 4).
Для объединения множеств выполняются следующие свойства.
1) Переместительное или коммутативное свойство: А ∪ В = В ∪ А.
2) Сочетательное или ассоциативное свойство:(А ∪ В)∪ С = А ∪ (В ∪ С).
3) А ∪ ∅= А (пустое множество является нейтральным элементом).
4) А ∪ U = U (универсальное множество является поглощающим элементом).
5) Если В ⊂А, то А∪В = В
Операции объединения и пересечения множеств связаны законами дистрибутивности или иначе распределительными свойствами:
(А ∪ В) ∩С = (А∩С) ∪ (В∩С) и (А∩В) ∪ С = (А ∪ С) ∩(В ∪ С).
П р и м е р 1. Пусть А – множество различных букв в слове «математика», а В – множество различных букв в слове «стереометрия». Найти пересечение и объединение множеств А и В.
Р е ш е н и е. Запишем множества А и В, перечислив их элементы: А = { м, а, т, е, и, к }, В = { с, т, е, р, о, м, и, я }. Буквы м, т, е, и принадлежат и множеству А, и множеству В, поэтому они войдут в пересечение этих множеств: А∩В = { м, т, е, и }. В объединение этих множеств войдут все элементы множества А и несовпадающие с ними элементы из множества В: А ∪ В = { м, а, т, е, и, к, с, р, о, я }.
П р и м е р 2. В классе английский язык изучают 25 человек, а немецкий – 27 человек, причем 18 человек изучают одновременно английский и немецкий языки. Сколько всего человек в классе изучают эти иностранные языки? Сколько человек изучают только английский язык? Только немецкий язык?

Р е ш е н и е. Через А обозначим множество школьников, изучающих английский язык, через В – множество школьников, изучающих немецкий язык. Изобразим эту ситуацию с помощью диаграммы. Два языка изучают 18 школьников, поставим это число в пересечение множеств А и В. Английский язык изучают 25 человек, но среди них 18 человек изучают и немецкий язык, значит, только английский язык изучают 7 человек, укажем это число на диаграмме. Рассуждая аналогично, получим, что только немецкий язык изучают 27 – 18 = 9 человек. Поместим и это число на диаграмму. Теперь известно количество элементов в каждой части множеств, изображенных на диаграмме. Чтобы ответить на главный вопрос задачи, нужно сложить все числа: 7 + 18 + 9 = 34. Ответ: 34 человека в классе изучают иностранные языки.
Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А \ В. Таким образом, по определению разности А \ В = { х | х ∈ А и х ∉В}.
Например, если А = { a, c, k, m, n } и В = { a, b, c, d, e }, то А \ В = { k, m, n }.
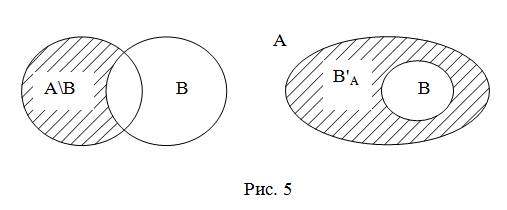
Если изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством множества А. В этом случае разность множеств А и В называют дополнением подмножества В до множества А и обозначают В'А. Дополнение можно изобразить как показано на рис. 5. Если В – подмножество универсального множества U, то дополнение подмножества В до U обозначают В'.
Например, если В – множество однозначных натуральных чисел, то В'– множество неоднозначных натуральных чисел, если С – множество равнобедренных треугольников, то С' – множество треугольников, у которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству обладают рядом свойств.
1) (А \ В) \ С = (А \ С) \ В.
2) (А∪В) \ С = (А \ С) ∪ (В \ С).
3) (А \ В) ∩ С = (А ∩С) \ (В ∩ С).
4) (А ∪ В)' = А' ∩ В'.
5) (А ∩ В)' = А' ∪В'.
Четвертое свойство формулируется так: дополнение к объединению двух множеств равно пересечению дополнений к этим множествам. Пятое свойство формулируется аналогично.
П р и м е р 1. А – множество натуральных чисел, кратных 3, В – множество натуральных чисел, кратных 5. Задать описанием характеристического свойства множество А \ В и назвать три числа, принадлежащих этому множеству.
Р е ш е н и е. По определению разность данных множеств состоит из натуральных чисел, кратных 3 и не кратных 5. Поэтому разности множеств А и В принадлежат числа 9, 24, 33.
П р и м е р 2. Найти дополнение к множеству А в множестве натуральных чисел, если:
а) А = { х | х = 2 k + 1, k ∈ N };
б) А = { х | х = 3 k, k ∈ ^ N }.
Р е ш е н и е. а) Числа вида х = 2 k + 1, k ∈ N представляют собой нечетные натуральные числа, следовательно, дополнение А' – это четные натуральные числа: А' = { х | х = 2 k, k ∈ N }.
б) В виде х = 3 k, k ∈ N записаны натуральные числа, кратные 3, или числа, дающие при делении на 3 остаток 0. В дополнение к этому множеству войдут числа, не кратные 3, или дающие при делении на 3 остаток 1 или 2. Запишем А' = { х | х = 3 k + 1 или х = 3 k + 2, k ∈ N о }.
Говорят, что множество Х разбито на попарно непересекающиеся подмножества или классы, если выполнены следующие условия:
1) любые два подмножества попарно не пересекаются;
2) объединение всех подмножеств совпадает с исходным множеством Х.
Разбиение множества на классы называют классификацией.
Классификацию можно выполнять при помощи свойств элементов множества. Если выбирается только одно свойство, то такую классификацию называют дихотомической. Например, натуральные числа можно разбить на четные и нечетные. Буквы русского языка можно разбить на гласные и не гласные. Вообще, если на множестве Х задано одно свойство А, то это множество разбивается на два класса: первый класс – объекты, обладающие свойством А, второй класс – объекты, не обладающие свойством А.
Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса. Например, на множестве натуральных чисел заданы два свойства: «быть кратным 2» и «быть кратным 3». При помощи этих свойств в множестве N можно выделить два подмножества А и В. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 6). Тогда в первый класс войдут числа, кратные 2 и 3, во второй – кратные 2, но не кратные 3, в третий – кратные 3, но не кратные 2, в четвертый – не кратные 2 и не кратные 3.
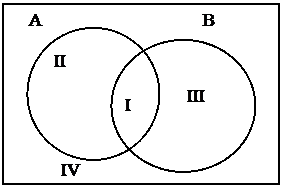
Рис. 6
П р и м е р 1. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:
а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;
б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?
Р е ш е н и е. а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.
б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.
Задания для самостоятельной работы по теме 2:
Приведите примеры множеств А, В, С, если отношения между ними таковы:
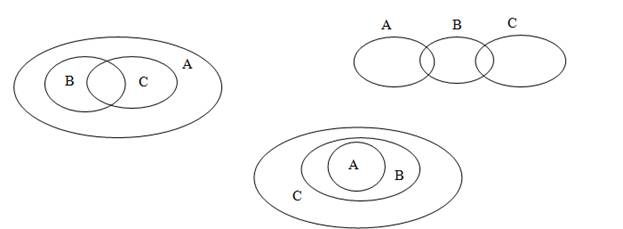
2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?
3. Даны множества А = { a, b, c, d, e, f, k } и В = { a, c, e, k, m, p }. Найдите А ∪ В, А ∩ В, А \ В, В \ А.
4. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N, A, B; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N; укажите характеристические свойства этих множеств.
5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.
6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø б)А U В=А
7. Пусть Х= { x 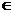 N/ 1
N/ 1  x
x  15}. Задайте с помощью перечисления следующие его подмножества:
15}. Задайте с помощью перечисления следующие его подмножества:
А – подмножество всех четных чисел;
В – подмножество всех нечетных чисел;
С – подмножество всех чисел, кратных 3;
D – подмножество всех чисел, являющихся квадратами;
E – подмножество всех простых чисел.
В каких отношениях они находятся?
Лекция 3. Математические понятия. Объем и содержание понятий. Определение понятий.
Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.
Существенное свойство - свойство, без которого объект не может существовать.
Несущественное свойство - свойство, отсутствие которого не влияет на существование объекта.
Для квадрата: АВСД существенные свойства: АВ = ВС = СД =ДА, АВ║ ДС, АД ║ ВС;
несущественные свойства: АВ, ДС - горизонтальны, АД, ВС - вертикальны. 
Если квадрат повернуть, сохранятся только существенные свойства, именно они и составляют понятие об объекте.
Рассмотрим пример для дошкольников, используя наглядный материал
Диалог:
- Опиши фигуру.
- Маленький черный треугольник.
- Большой белый треугольник.
- Чем фигуры похожи?
- Формой.
- Чем фигуры отличаются?
- Цветом, величиной.

- Что есть у треугольника?
- 3 стороны, 3 угла.
Таким образом, дети выясняют существенные и несущественные свойства понятия "треугольник". Существенные свойства - "иметь три стороны и три угла", несущественные свойства - цвет и размеры.
Совокупность всех существеннных свойств объекта называют содер-жанием понятия.
Совокупность всех объектов, обозначаемая одним термином, составляет объем понятия.
Например, содержание понятия «квадрат» - это совокупность всех существенных свойств, которыми обладают квадраты, а в объем этого понятия входят квадраты различных размеров.
Итак, любое понятие характеризуется:
- термином (название);
- объемом (совокупность всех объектов, называемых этим термином);
- содержанием (совокупность всех существенных свойств объектов, входящих в объем понятия).
Между объемом понятия и его содержанием существует связь: чем "больше" объем понятия, тем "меньше" его содержание, и наоборот. Объем понятия «треугольник» "больше", чем объем понятия "прямоугольный треугольник", так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия "треугольник" "меньше", чем содержание понятия "прямоугольный треугольник", так как прямоугольный треугольник обладает всеми свойствами любого треугольника и еще другими свойствами, присущими только ему.
^ ОПРЕДЕЛЕНИЕ ПОНЯТИЙ
Для распознавания объекта необязательно проверять у него все существенные свойства, достаточно лишь некоторых. Этим пользуются, когда понятию дают определение.
Определение понятия – это логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. Определение понятия позволяет отличать определяемые объекты от других объектов. Так, например, определение понятия "прямоугольный треугольник" позволяет отличить его от других треугольников.
Различают явные и неявные определения. Явные определения имеют форму равенства двух понятий. Одно из них называют определяемым другое определяющим.
Например: "Квадрат – это прямоугольник, у которого все стороны равны". Здесь определяемое понятие – «квадрат», а определяющее - "прямоугольник, у которого все стороны равны".
Самый распространенный вид явных определений - это определение через род и видовое отличие. Приведенное выше определение квадрата относится к таким определениям. Действительно, понятие "прямоугольник", содержащееся в определяющем понятии, является ближайшим родовым понятием по отношению к понятию "квадрат", а свойство "иметь все равные стороны" позволяет из всех прямоугольников выделить один из видов - квадраты.
Следует иметь в виду, что понятия рода и вида относительны. Так, "прямоугольник" – это родовое к понятию "квадрат", но видовое по отношению к понятию «четырехугольник».
Кроме того, для одного понятия могут существовать несколько родовых. Например, для квадрата родовыми являются ромб, четырехугольник, многоугольник, геометрическая фигура. В определении через род и видовое отличие для определяемого понятия принято называть ближайшее родовое понятие.
Таким образом, определение через род и видовое отличие имеет следующую структуру:
Определяемое = Род + Видовое
К явным определениям предъявляются определенные требования.
1) Определение должно быть соразмерным. Например, нельзя говорить, что окружность – это линия, которая начинается и кончается в одной точке. Этому определению удовлетворяют много линий, не являющихся окружностями.
2) В определении (или их системе) не должно быть порочного круга. Это означает, что нельзя определять понятие через само себя. Например, содержит порочный круг определение: «Касательная к окружности – это прямая, которая касается окружности».
3) Определение должно быть ясным и минимальным. Нельзя определять прямоугольник как параллелограмм с прямым углом, если понятие «параллелограмм» еще не рассмотрено. В определении не должно быть лишних свойств. Например, неправильным будет определение: «Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны и равны». Равенство сторон в определении не нужно указывать, так как оно вытекает из свойств параллелограмма.
Существуют неявные определения. В их структуре нельзя выделить определяемое и определяющее понятия. Среди них выделяют контекстуальные и остенсивные определения.
В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл вводимого понятия. Например, в начальной школе понятие уравнения можно ввести так: «К какому числу надо прибавить 6, чтобы получилось 15? Обозначим неизвестное число латинской буквой х (икс): х + 6 = 15 – это уравнение. Решить уравнение – значит найти неизвестное число. В данном уравнении неизвестное число равно 9, так как 9 + 6 = 15».
Остенсивные определения – это определения путем показа. Например, таким способом можно определить в начальной школе понятия равенства и неравенства:
3·8 > 2·8 5·8 = 40
65 + 9 < 82 – 5 6·8 = 5·8 + 8
48: 8 < 48 18: 9 = 16 – 14
Это неравенства. Это равенства.
Контекстуальные и остенсивные определения используются на ранних стадиях изучения предмета, когда обучаемые не обладают достаточными теоретическими знаниями.
П р и м е р 1. Назовите несколько свойств, принадлежащих содержанию понятия «треугольник». Принадлежит ли содержанию этого понятия свойство «иметь две равные стороны»?
Р е ш е н и е. В содержание понятия «треугольник» входят только те свойства, которые являются общими для всех треугольников, например, такие: 1) имеет три вершины, 2) имеет три угла, 3) имеет три стороны, 4) ограничен замкнутой ломаной линией. Свойство «иметь две равные стороны» в содержание понятия «треугольник» не входит, так как этим свойством обладают не все треугольники.
^
Задания для самостоятельной работы по теме 3:
1. Каков объем понятий: «цифра», «автомобиль», «снегурочка», «волк», «столица России», «двузначное число».
2. Решите анаграммы. Исключите лишнее слово. Ответ обоснуйте:
Каут, кабоса, цикурка, кайнеди;
Релоказ, начик, меро, лекосо;
Вианд, лексор, слот, самик, фебут.
3. Дополните определение:
Портной – это …., который шьет одежду.
…. – это человек, который рисует картины.
Врач - ….
Масленка - …
Улей - …






