Мынандай тәсілдер бойынша іске асады:
1º. Теңдеудің екі жақ бөлігін де бірдей негізге келтіру.
2º. Ортақ көбейткішті жақша сыртына шығару.
3º. Жаңа белгісіз енгізу және одан арылу.
4º. Логарифмдеу және потенцирлеу.
5º. Графиктік тәсіл.
6º. Анықтаманы пайдалану.
Мысалдар.
Мына теңдеулерді шешу керек.
76. 27=[0,(3)]6-x
Шешуші: Мұны төмендегіше түрлендіруге болады: 27=(1/3)6-x  27=3x-6 немесе
27=3x-6 немесе

Жауабы: x=9
77. 
Шешуі:  Былай қайта жазайық:
Былай қайта жазайық: 
Сонда 
Егер  десек,
десек,  болады. Жаңа белгісізден арылсақ: 1)
болады. Жаңа белгісізден арылсақ: 1) 
Сонда 
Жауабы: 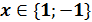
78. 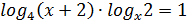
Белгісіздердің мүмкін мәндері x>0, x  0;1 теңсіздіктері бойынша анықталады. х осы жиында жатыр деп есептеп, төмендегіше түрлендірейік. Логарифм астындағы сан мен логарифм негізінен бірдей көрсеткішті түбір табу амалын орындағаннан логарифмнің мәні өзгермейтіндіктен
0;1 теңсіздіктері бойынша анықталады. х осы жиында жатыр деп есептеп, төмендегіше түрлендірейік. Логарифм астындағы сан мен логарифм негізінен бірдей көрсеткішті түбір табу амалын орындағаннан логарифмнің мәні өзгермейтіндіктен
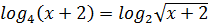 немесе
немесе  болғандықтан, берілген теңдеу мына түрге келеді:
болғандықтан, берілген теңдеу мына түрге келеді:  x>0 екенін ескеріп, мұны квадраттап
x>0 екенін ескеріп, мұны квадраттап
 екенін табамыз.
екенін табамыз.
х2 анықталу облысында жатқандықтан бастапқы теңдеуге қойып тексерейік. x2=2- шешім болатындығы анықталады. Есепті анықтаманы пайдаланып та шешуге болады.
Жауабы: x=2
79. 
Шешуі:

немесе 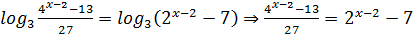
Егер  болады. х белгісізгеоралсақ
болады. х белгісізгеоралсақ
1) 
2) 
Жауабы: 
80. (sinx 
Шешуі: 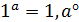 =1 екендігін ескеріп былай деуге болады:
=1 екендігін ескеріп былай деуге болады:
1) 
2) 
Жауабы: 
Есепті басқа да тәсілдермен шешуге болады.
81. xlog2x+2=3
Нұсқау. 2 негізі бойынша логарифмдеңіз.
Жауабы:  ,
, 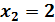
82.  +
+ 
Нұсқау. 3 негізіне көшіңіз. Егер теңдікті  – ке қысқартсаңыз, оның нөлге тең болу жағдайын ескеріңіз.
– ке қысқартсаңыз, оның нөлге тең болу жағдайын ескеріңіз.
Жауабы: 
83. 
Нұсқау. Бірнеше рет потенцирлеңіз немесе логарифм анықтамасын пайдаланыңыз.
Жауабы: 
84. 
Жауабы: 
85. 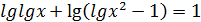
Жауабы: 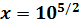
86. 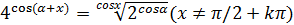
Нұсқау. Бірдей негізге келтіріп, теңдіктің сол жақ бөлігін қосындыға түрлендіреміз.
Жауабы: 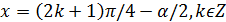
Тригонометриялық теңдеулерді шешу тәсілдері
Б і р т е к т і т е ң д е у л е р т ә с і л і.
Синус пен косинустың дәрежелері бірдей болып бос мүшесі болмаса, ондай теңдеулерді біртекті теңдеулер дейміз.
87. Мына теңдеулерді шешіңіз:
 Бұл бірінші дәрежелі біртекті теңдеу.
Бұл бірінші дәрежелі біртекті теңдеу.
Мұндай теңдеулерді cosx-ке мүшелеп бөліп шешеді. Өйткені егер cosx=0 болса, түбір жоғалмайды. Себебі sinx=±1 болып, atgx+в=0 теңдеуінің сол жағы нөлге айналмайды.
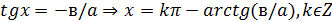
Екінші дәрежелі біртекті теңдеу  осы тәсілмен шешіледі.
осы тәсілмен шешіледі.
 - ге мүшелеп бөліп
- ге мүшелеп бөліп 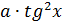 +в
+в  квадрат теңдеуге келеміз. Егер бұл теңдеудің түбірлерін х1 мен х2 десек, енді tgx=x1 мен tgx=x2 теңдеулерін шешу ғана қалады. Мұнан
квадрат теңдеуге келеміз. Егер бұл теңдеудің түбірлерін х1 мен х2 десек, енді tgx=x1 мен tgx=x2 теңдеулерін шешу ғана қалады. Мұнан
 және
және  -ке берілген теңдеудің сол жақ бөлігін мүшелеп бөлу үшін оның ортақ көбейткіші болмауы тиіс.
-ке берілген теңдеудің сол жақ бөлігін мүшелеп бөлу үшін оның ортақ көбейткіші болмауы тиіс.
88. 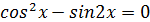
 болғандықтан, бұл екінші дәрежелі біртекті теңдеу. Мұны ескергенде
болғандықтан, бұл екінші дәрежелі біртекті теңдеу. Мұны ескергенде
 . Ортақ көбейткіш cosx болғандықтан оны cosx-ке бөлсек, теңдеудің
. Ортақ көбейткіш cosx болғандықтан оны cosx-ке бөлсек, теңдеудің  түбірін жоғалтып аламыз. Неге? Себебі
түбірін жоғалтып аламыз. Неге? Себебі
1) 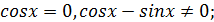
2)  жағдайын қарастырсақ, бұдан
жағдайын қарастырсақ, бұдан 
Біртекті теңдеуге келтіру тәсілі.
89.  теңдеуін d-ні
теңдеуін d-ні  деп өзгертсек, біртекті теңдеуге келеді. Мұнда ұқсас мүшелерді жинақтау керек.
деп өзгертсек, біртекті теңдеуге келеді. Мұнда ұқсас мүшелерді жинақтау керек.
Мысал.
90.  теңдеуін шешу керек.
теңдеуін шешу керек.
Шешуі: Біртекті теңдеуге келтірейік:

Ұқсас мүшелерін жинақтағаннан кейін  -ге бөлейік.
-ге бөлейік.
Сонда 
Мұнан  Z
Z
Жаңа белгісіз енгізу және одан арылу тәсілі
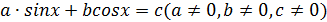 (1)
(1)
Мұндай теңдеулерді  десек (1) теңдеу
десек (1) теңдеу  (2) түріне келіп
(2) түріне келіп  табылады.
табылады.
Зерттеу.
a)Егер  болса және b+c
болса және b+c 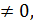 онда (2) теңдеудің нақты түбірлері бар. Ол
онда (2) теңдеудің нақты түбірлері бар. Ол

б)Егер  болса, онда (1) теңдеудің нақты шешімі жоқ;
болса, онда (1) теңдеудің нақты шешімі жоқ;
в)Егер b+c=0 болса, (2) теңдеу сызықтық t= -b/c теңдеуіне түрленеді де, (1) теңдеудің шешімдері былай болады: 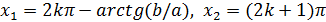
Пайдалы ауыстыру тәсілі. Мұнда тригонометриялық функциялар арасындағы теңбе-теңдіктер пайдаланылады.
Мысалдар.
91. sinx-cosx=1 теңдеуін шешіңіз.
1 тәсілі. cosx-ті sinx арқылы өрнектейік:




Мұнан: не sinx=0,  не
не 
Квадраттау нәтижесінде бөгде түбір пайда болуы мүмкіндігінен табылған түбірді тексеру керек. Тексерсек n-тақ екендігін айқындаймыз. Ақырында есеп жауабы  және
және  екендігі табылады.
екендігі табылады.
2-тәсілі. Берілген теңдеуді квадраттап, кейін  -ке көбейтсек, теңдеу біртекті теңдеуге келеді. Оны шеше аламыз.
-ке көбейтсек, теңдеу біртекті теңдеуге келеді. Оны шеше аламыз.
3-тәсілі. 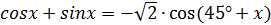 формуласын пайдалануға болады.
формуласын пайдалануға болады.
Бірдей аргументке келтіру тәсілі.
92. 
Шешуі.
Теңдеудің екі жақ бөлігінде де квадраттап  екенін ескерсек, бастапқы теңдеу
екенін ескерсек, бастапқы теңдеу  теңдеуіне келеді немесе
теңдеуіне келеді немесе
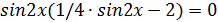 .
.
Мұнан:
1)не 
2)не 
Жауабы: 
93. 
Шешуі. Берілген теңдеуді төмендегіше түрлендірейік:
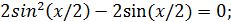
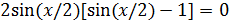
Мұнан  екенін табуға болады.
екенін табуға болады.
94. 
Шешуі:

Сонда 
Ортақ көбейткішті жақша сыртына шығарсақ былай болады:

Мұнан
1) 
2) 
Соңғы теңдеудің сол жағын көбейтіндіге келтірсек
 болады.
болады.
Жауаптары осы.
95. 
Шешуі:

Былай топтайық:

Мұнан

cos3x=0 мен cos3x=cosx теңдеулерін шешіп,  екенін табамыз.
екенін табамыз.
Жауабы: 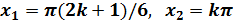
Дәрежені кеміту тәсілі
96. 
Шешуі: 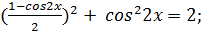
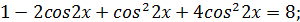

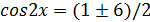
Мұнан
1) 
2)  - бұлай болмайды, өйткені
- бұлай болмайды, өйткені 
97. 
Нұсқау. Квадрат түбір тауып, екі теңдеулер сериясын шешіңіз және  мен n мәндеріне сәйкес түбірлерді зерттеңіз.
мен n мәндеріне сәйкес түбірлерді зерттеңіз.
Жауабы: 






