Жаттығулар:
3. 
8.tg 
4.sin 
9.tg 
5. 
10.tgx>cosx
6.4sin3x<2sinx+cos2x 11. 
7.(
0 
II.Көлемге арналған есептер
1. Кейбір негізгі есептер.
1. Жазық бұрыштары 
берілген үш жақты бұрыштарын табыңдар.
Берілгені: SABC-үш жақты бұрышы, 
Табу керек: 
-екі жағының арасындағы
кез-келген сызықтық бұрышын.
Шешу. Алдымен үш жақты бұрыштың екі
жақты сызықтық бұрышы,екі жақтың
ортақ қырының кез-келген нүктесінен әрбір
жағында жататындай етіп жүргізілген перпендикулярдың арасындағы бұрышпен өлшенетіндігән еске ала отырып,
сондай бұрыштардың үшеуінің бірі 
салайық (4-сурет). Ол үшін ASC мен BSA жақтарының SA ортақ қырының кез-келген М нүктесін алайық. 
жүргізсек, SA қыры NMD жазықтығына перпендикуляр болады.
Уақытша 
бұрыштарының арасында төмендегідей байланыстар бар.
1) SMN/ 
=xsec 
2) SMD/ 
=xsec 
Кез келген үшбұрыштың бір қабырғасының квадраты, оның былайғы екі қабырғасының квадраттарының қосындысынан сол қабырғалармен олардың арасындағы бұрыштың косинусының екі еселенген көбейтіндісін шегергенге теңдеген косинустар теоремасы бойынша 
оларды өзара теңестірейік:
Бұдан
Мұның алымын да, бөлімін де cosα2cosα3 
0-ге көбейтіп, тангенстер мен секанстерді синус пен косинус арқылы жазып, қысқартсақ, формула мына түрге келеді:
(1)
Осы сияқты есептеп мына формулаларды да табуға болады:
Бұларды логарифмдеуге ыңғайлы түрге келтірейік:
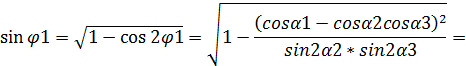
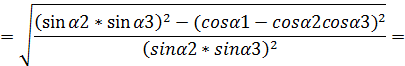
радикаластындағы өрнектің алымы екі санның квадраттарының айырымы, олардың негізі мен түйіндісіне жіктеп, әрбір жақшаның ішіндегі өрнекті қайта топтап,
және
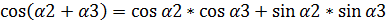
қосу формулаларын пайдаланайық
Пайдалануға ыңғайлы болу үшін былай жазайық:
Мұндағы
Q= 
Егер 
болса, 
болып, формула
(2)
түріне келеді. Логарифмдеуге ыңғайлы түрге келтірейік:
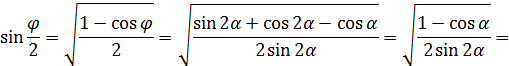
(2’)
Бұл формулалар үш жақты бұрыштың төбесіндегі жазық бұрышы мен бүйір қыры екі жақты бұрышының арасындағы байланысты көрсетеді. Ескере жүретін мәселе бұл келтірілген (2), (2’) формулаларын үшбұрышты пирамидаға арналған есептерді шешкенде толығынан пайдалануға болады. Мұны есте ұстауымыз керек! (1) формула үш жақты бұрыш үшін косинустар теоремасы деп аталады. Бұл формуланың басқаша қорытылып шығарылуын «Математика в школе» журналының 1970 жылғы №8 қарауыңызға болады.
2. Үш жақты бұрыштың қырының жазық бұрыштың жазықтығымен жасайтын бұрышы жазық бұрыштары арқылы табыңдар.
Берілгені: 
Табу керек: 
AD түзуінBSC жазықтығына,SA қырына
ACB жазықтығын перпендикуляр етіп
жүргізейік. Әзірше 
деп алайық.
SABCпирамидасының көлемін екі түрлі
әдіспен есептеуге болады: 1) пирамиданың
биіктігі ретінде 
, табаны ретінде CAB-ны, AD кесіндісін оның биіктігі, ал
CSB-ны деп қарастырсақ болғаны. Сонда
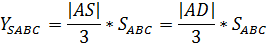
Мұндағы:
келісіміміз бойынша
Бұдан
(3)
Бірінші есеп бойынша
3. lgb+ 
екенін дәлелдеңіз.
Шешуі.
lgb* 
4. 
теңдеуін шешу керек.
1-тәсіл. х-тің мүмкін мәндер жиыны
90 
теңсіздігімен анықталады, өйткені: біріншіден, х 
х-тің бұл мәндерінде тангенстің не котангенстің мәні болмайды; екіншіден, тангенс пен котангенстің екеуі де оң сандар, яғни х бірінші не үшінші ширекте аяқталуы керек, өйтпесе олардың логарифмі болмайды.
lgtgx пен lgctgx
өзара кері шамалар болғандықтан, (1) бойынша
y+ 
түрінде жазуға болады.
Теңсіздік өзінің ең кіші мәнін у 
1 болғанда қабылдайды.
Демек,
1
2-тәсіл. Есепті у 
белгілеумен де шешуге болады. Неге?
4. 2х 
екенін дәлелдеңіз.
Шешуі. 
екені шығады. Берілген теңсіздіктің оң жағы 2-ден кем емес, себебі олардың көбейтіндісі бір.
Сонымен, бастапқы теңсіздіктің сол жағы 2-ден артық емес те, оң жағы 2-ден кем емес. Мұндағы екі жағдайдың біріншісі: теңсіздіктің ақиқат екендігіне келтіреді, ал екіншісі: олар тең болып қалуы мүмкін бе деген сұраққа тіреледі. Сұраққа жауап беру үшін
2 
системасының үйлесімділігін дәлелдеу керек. Бірінші теңдеуден х 
екенін табамыз. Бұл мәндерде екінші теңдеу ақиқат емес. Демек, берілген теңсіздік орынды.
5. х пен 
-нің қандай нақты мәндерінде
(1)
теңсіздігі орындалады?
Шешуі: Егер 
десек, онда 
Сонда бастапқы теңсіздік
у+ 
(2)
түріне келеді. Бұл арада мынандай екі ескерту жасауға болады. Біріншіден, у+1/у санымен у санының таңбалары бірдей, екіншіден 
өйткені 
. Сондықтан, 1) егер у+1/у болса, (2) тек у+1/у 
және 
болғанда орындалады, басқаша айтқанда х 
болғанда орындалады. х пен 
осы мәндерінде теңдік орындалады;
2)Егер у+1/у<0 болса, яғни у<0 болса, онда у+1/у 
-2 және (2) теңсіздік барлық мәнінде де орындалады. Олай болса (2)-ге эквивалентті (1) теңсіздік орындалады.
3) Егер 0<х<1 болса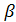 
–нің кез келген нақты мәнінде, бастапқы теңсіздік ақиқат.
Жауабы:
1) x=2, 
2) 
3) 
7. Оң х пен nнатурал саны үшін
екеніндәлелдеңіз.
Шешуі. 1-тәсіл.
Егерn-тақ сан болса, онда теңсіздіктің сол жақ бөлігіндегі ең соңғы қосылғыш орнында х+1/х болады. Ал оң жақ бөлігінде (n+1)/2 қосылғыш болып, қосындысы n+1 болады.
2-тәсілі. Есепті математикалық индукция методымен де шешуге болады.
Мұндай есептер тізімін соза беруге болар еді, бірақ осының өзі-ақ жоғарыдағы методикалық пікірдің ұстамдылығы айғақ.
Жаттығулар:
8. Кез келген a мен b оң сандары үшін
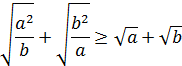
екенін дәлелдеңіз.
Нұсқау. Теңсіздікті 
, ал 
дептүрлендіріңіз де 
қорытынды шығарыңыз. Әрі 
екені белгілі.
9. 
екенін дәлелдеңіз.
Нұсқау. Радикалды 
түрінде жазыңыз.
10. 
екенін дәлелдеңіз.
Нұсқау. Теңсіздіктің сол жақ бөлігінің алымын да, бөлімін де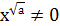 
санына бөліңіз. Ойланыңыз!
11. 
теңдеуін шешіңіз.
Нұсқау. (1) тексеріп, (2)- ні пайдаланыңыз. Қосындының минимумын қараңыз.
12. a>1, b>1 және с>1 үшін мына теңсіздікті дәлелдеңіз:
Нұсқау. Квадрат жақшаны ашып, түрлендіріңіз.
13. Теңдеуді шешіңіз:
+2=0
Нұсқау. 3 пен 4 жақша сыртына шығатындай етіп топтаңыз, теңдік орындалу үшін
болу керектігін ескеріңіз.
14. Теңдеуді шешіңіз:
Нұсқау. Есепті қосындының тангенсінің формуласын пайдаланып та шешуге болады.
15. Теңдеуді шешіңіз: tg 
Нұсқау. 
екенін ескеріңіз.
16. Системаны шешіңіз:
tgx+ctgx=2
sin2x+cos2x=1
Нұсқау. tgx=1
sin2x+cos2x=1
үйлесімді система екенін ескеріңіз.
Жауабы: х= 
17. A, Bжәне C– сүйір бұрышты үшбұрыштың ішкі бұрыштарының шамасы болса, онда
tg 
екенін дәлелдеңіз.
18. Теңдеуді шешіңіз: 
Нұсқау. 
tg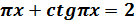 
системасын пайдаланыңыз. Неге?
19. Теңдеуді шешіңіз: 
Нұсқау. 
екенін ескеріңіз.
20. Аргументтің қандай мәнінде 
теңсіздігі орындалады?
Жауабы: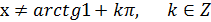 
21. Системаны шешіңіз:
Жауабы: (6;6)
22. Теңдеуді шешіңіз:
tg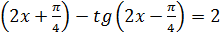 
Жауабы: х 
23. 
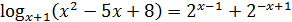
Жауабы: х=3
Нұсқау. Теңсіздіктің сол жақ бөлігі 2-ден кем емес. Себебі не? 
. Неліктен?
Бұл бір тәсілмен шешілетін есептердің бірінші мысалы. Келтірілген есептер түгелімен дерлік қиынырақ есептер. Мұндай типтегі есептерді тану үшін (теңсіздік) белгісінен кейін 2, 4, 6, 8....., 
1/2, ¼, 1/8,…, 
немесе көбейтінді 1-ге тең болуына көңіл аудару керек. Әрине, ол осы тәсілмен барлық есептерді шығаруға болады деген қате пікірге әкелмеуі тиіс. Дегенмен, тәсілді пайдаланып көруге болады. Бір тәсілмен шешілетін есептерді танудың екінші мысалын қарастырайық.
§3. Жаңа белгісіз енгізу тәсілі
Мына теңдеулер мен системаларды шешу керек:
24. 
25. 
26. 
27. 
28. 
29. 
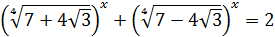
30. 
31. 
32. 
33. 
34. 
35. 2 
+ 
=9
36. 
37. 
38.{x+xy+y=7
Келтірілген теңдеулердің әрқайсысын түрлендіру көмегімен х функциясы болатын жаңа белгісізге қарағанда басқа теңдеуге келтіруге болады. Оны шешіп, бастапқы белгісіз х-ке көшу керек. Кейбір оқушылар соңғы теңдеуден жаңа белгісізді табумен шектеледі де одан арылмайды. Шешуді ақырына дейін жеткізбейді. Сақ болу керек.
Біріншіден, олардың түр ұқсастығы, екіншіден дәреже негіздерінің ұқсастығы не бірдейлігі, көпмүшелердің симметриялығы немесе белгісізі бар мүшелердің бірдейлігі. Теңдеулерді шешуге қарастырайық.
(24)-те теңдеуді 
деп өзгертіп, (25)-те 
деп өзгертіп, 
(26)-да 
деп өзгертіп, 
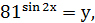(27)-де 
деп өзгертіп, 
(28)-де, (29)-да сәйкесінше 
(30)-да радикалдың біреуін у деу керек. (31)-де 
деп жазып, жақша ішіндегі өрнекті у деу керек. (32)-де 
ауыстыруын қолданып, 0-ге теңегеннен кейін lgx=t десе болады. (35)-те 3х2-5х+4=tдеу керек. (37)-де радикалдың біреуін у десе болады. (38)-де х+у=v, xy=vдесек,
қосымша системасына келеміз. Мұның
дегенекі шешімі бар. Демек, бастапқы системаның шешімдер жиыны
системасының шешімдері жиынының бірігуіне тең болады:
Жауабы: {(1;3); (3;1)}
Қалғандары да осы сияқты шешіледі. Жоғарыда көрсетілген кейбір есептер басқа да тәсілдермен шешіледі. Ойланыңыздар!
39. Егер квадрат теңдеудің түбірлері х1 мен х2 болса және
берілсе, онда квадрат теңдеуді құру керек.
40. 
Нұсқау. Системаның екінші теңдеуінен ху-ті жақша сыртына шығарып. х+у=u, ху=u алмастыруын жасаңыз.
Жауабы:{(5;1); (1;5); (3;2); (2;3)}
41. 
Нұсқау. 
белгілеуін енгізіңіз
Жауабы: {(
; 
); (10 
); (
)}
42. 
Нұсқау. 2х+3у 
алмастыруын жасаңыз.
Ескерту. 39-46 системалардағы х пен у-тің өзара орнын ауыстырғаннан көпмүшенің түрі өзгермейді. Мұндай көпмүшелер симметриялы делінеді. х+у, х*у – симметриялы көпмүшенің ең қарапайым түрі. Симметриялы көпмүшеден құралған алгебралық системаларды жаңа белгісіз енгізу арқылы шешу оңтайлы.
43. 
х+у=20
44. 
45. 
Нұсқау. 
екенін ескеріп, теңдеулердің екі жақ бөліктерін де
ху-ге бөліңіз. Енді х+1/х 
де.
Жауабы: 
46. 
х+у+ху=9
Нұсқау. Системаның бірінші теңдеудін квадраттап, 
екенін ескеріңіз, әрі х+у=u, x*y=v деп белгілеңіз.
Жауабы: {(4; 1); (-9; -9/4)}
Кейбір есептерді тікелей белгілеу арқылы да шешуге болады.
Мысалдар.
47. 
Нұсқау. 1-тәсіл. tgx>0 болуы керектігін ескеріп, радикалдарды u мен vдеп белгілеңіздер.
Жауабы: x=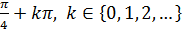 
2-тәсіл. 
формуласын пайдаланып, берілген теңдеудің екі жақ бөлігін декуб дәрежеге шығарсақ екенін ескерсек, соңғы өрнек 
түріне келеді. Мұны шешу оңай.
48. 
Нұсқау. Радикалдарды u және v десек, жаңа пайда болған системадан uv-ні табу керек.
49. 
Нұсқау. 
+17=t2 деукерек.
Жауабы:х= 
50. х-у= 
Нұсқау 
депбелгілеңіз.
Жауабы: {(216; 27); (-27; -216)}
51. 9* 
Нұсқау. 
деңіз.
Жауабы: х1=3, x2=lg(250/3)
52. 
Нұсқау. 
Жауабы: х=1
53. 
Нұсқау. 1-тәсілі. 
деп белгілеу керек. Белгісіздің мүмкін мәндерінің анықталу облысы х>0 теңсіздігімен анықталады. х осы облыста жатыр деп есептеп, төмендегідей түрлендіру жүргіземіз.
Егер 
қатысын еске алсақ, онда
болады.
Демек бастапқы теңдеу мына түрге келеді:
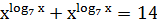
немесе
Соңғы теңдікті 7 негізі бойынша логарифмдесек
x=1⇒ log7x=±1
Мұнан
1) log7x=1⇒x1=7; 2) log7x= -1⇒x2=1/7
Жауабы: х1=7 x2=1/7
54. 
+ 5lg (1-x)=6
Нұсқау: радикалдыt деңіз
Жауабы: х= -9
55. 6log6x+ xlog6x=12
Нұсқау: 53 есеп сияқты шешіңіз.
Жауабы: x1=6, x2=1/6
