⇒ 
⇒ x≥6.
Берілген теңдіктің екі жақ бөлігін де квадраттайық. Сонда ықшамдағаннан кейін 
екені шығады. Бұл теңдіктің сол жақ бөлігі 4 (x-3) ≥0⇒x≥3 шартын қанағаттандыруы тиіс. Олай болса мына система орынды:
. 
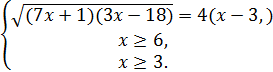
Системаның бірінші теңдігін квадраттап, ықшамдап, пайда болған теңдеуді шешсек,
х1=-18/5 және х2=9 екенітабылады.
Демек,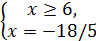 
және 
Мұны біріншісі үйлесімсіз система. Олай болса х=9 теңдеудің шешімі.
Түйіндестер тәсілі.
x 
t= (x-15)/ 
t- мәнін орнына қойып түрлендірсек, 5х2-27х-162=0 теңдеуіне келеді. Мұнан х1=9, х2=-18/5 табылады. х мәндерін бастапқы теңдеуге қойып тексеру арқылы х=2 шешім екендігіне көз жеткіземіз.
69. 
Шешуі 1 тәсілі. Белгісіздің мүмкін мәндерінің жиыны x2-6 ≥ 0 ⇒ |x |≥ 
теңсіздігімен анықталады.Сонда берілген теңдеу мына аралас системаға эквивалентті:
Радикалдың арифметикалық түбірі қарастырылатындықтан,
12-х2≥ 0⇒|x| ≤ 
Егер системаның бірінші теңдеуін квадраттайтын болсақ, белгісіздің анықталу облысы кеңейіп бөгде түбір пайда болуы мүмкін. Дегенмен осылай орындайық:
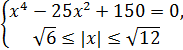
немесе
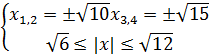
Мұнда ± 
системаның екінші шартымен қайшылықта. Олай болса, тек 
берілген теңдеудің түбірі.
2 тәсілі.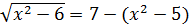 
түрінде жазып дәрежелеу арқылы шешуге де болады.
3 тәсілі. 
түйіндесін пайдалансақ, түрлендіру нәтижесінде
х4-25х2+150=0 биквадрат теңдеуіне келеді.
70. 4 
1 аралас система тәсіл. Радикалды бөлек жазсақ, ол мына аралас системаға эквивалентті:
немесе
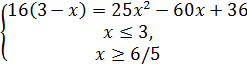
немесе
және 
Мұнан х1 берілген теңдеудің шешімі екендігі шығады.
Түйсіндестер тәсілі.
Нұсқау. 4 
деу керек.
Жаңа системадан t=(12-16x) / 5x екені табылады. t-нің мәнін орнына қойып, әрі былай түрлендірейік:
- 
12=5x-(12-16x) / 5x
Ортақ бөлімге келтірсек, ықшамдағаннан кейін 25x2-44x-12=0 теңдеуі шығады.
Мұнан х1=2, x2=-6/25
Мұның x1=2 түбір екендігін анықтауға болады
71. 
(1+cosx)=2
Нұсқау. Шешуі: 1 аралас система тәсілі. Берілген теңдеу 
cos(x/2) 
аралас системасына келеді. Мұнда 1+cos=2cos2(x/2)>0 екенін ескердік. Соңғы системаны шешсек, x= 
2 тәсілі. Берілген теңдеуді шешу үшін 
түрінде жазып, мұны 
негізі бойынша потенцирлейік. Сонда 1+сosx = (
Егер cosx= 
екенін ескерсек, соңғы теңдеу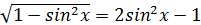 
түріне келеді. Квадраттасақ
1- 
= 4 
немесе 
Мұнан 1)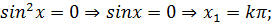 
2)4sin2x-3=0⇒sinx=± 
⇒x2= 
+2kπ, k=0, 1, 2……
Бұл арада синустың теріс мәні алынбайды, өйткені логарифм негізі теріс сан бола алмайды.
Жаттығулар:
72. 
Нұсқау: 
-ді жекелеу керек. Жауабы: 
73. 
Нұсқау: Белгісіздердің мүмкін мәндерінің жиыны. 
теңсіздігімен анықталады. Егер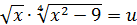 
десек, берілген теңдеуден u1=2, u2= - 1 табылады. Сосын белгісіз х-ке оралып, екі аралас система құру керек.
Есепті белгілеу не түйіндестер тәсілімен шешіп көріңіз.
74. 
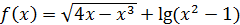функциясының анықталу облысын табыңыз.
Нұсқау. Ол мына аралас системаның шешумен эквивалентті:
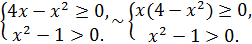
Жауабы: 
75. 
теңдеуін шешіңіз.
Нұсқау. Екінші радикалды оң жағына шығарып, екі рет квадраттайық та радикалды жекелеп тағы квадраттасақ х1=2, x2=-538/51 табылады. Екінші түбірді аралас система арқылы тексеріңіз. Сонда тек x1=2- шешім екендігі табылады.
