Цей метод полягає в тому, що застосовуючи замість змінних різні підстановки і комбінуючи одержані рівняння з вихідним, одержуємо алгебраїчне рівняння відносно шуканої функції. Слід підкреслити, що при використанні методу підстановок можуть виникнути зайві розв'язки. А тому перевірка є обов'язковою.
Приклад 2.1. Розв'язати функціональне рівняння
| (2.1) |
(х + у) + (х -у) = 2 
Розв'язання Застосувавши послідовно метод підстановки
одержуємо відповідно такі рівняння:
,
або
(2.2)
де 
Розв'язавши систему рівнянь (2.2) як систему лінійних алгебраїчних рівнянь з невідомими 
одержимо
. (2.3)
Таким чином, доведено, що функція 
є розв'язком функціонального рівняння (2.1) тільки тоді, коли вона має вигляд (2.3).
Покажемо, на завершення доведення, що функція 
де 
— константи, є розв'язком (2.1).
Дійсно,
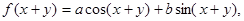
Приклад 2.2. Розв'язати рівняння
(2.4)
Розв'язання. Застосувавши метод підстановки 
з рівняння (2.4) одержуємо:
де 
Розв'язавши (2.5) як систему лінійних алгебраїчних рівнянь з невідомими 
і 
, дістанемо
(2.6)
Функція (2.6) задовольняє функціональне рівняння (2.4), що легко встановлюється перевіркою.
Аналіз розв'язань рівнянь (2.1) і (2.4) приводить до висновку, що аналогічні підстановки можна застосувати також і до інших рівнянь виду
Приклад 2.3. Розв'язати функціональне рівняння
(2.7)
Розв'язання Поклавши в (2.8) х = у = 0, одержимо
Звідси 
Застосувавши підстановку х = 0,у = 
, матимемо
(2.)
Для у = 0 з урахуванням (2.8) маємо
і за індукцією для будь-якого натурального п
(2.9)
Підставивши в (2.8) у = 2, знаходимо
За формулою (2.10) 
Легко побачити, що 
Із (2.8) одержуємо 
Звідси 
Оскільки довільне >1 зображується у вигляді 
, то при 
Якщо , то, вибравши 
таким чином, щоб 
>1, і застосувавши (2.10), матимемо
Отже, 
для всіх дійсних х.
Розділ 3 Ітераційний метод
Познайомимось з ітераційним методом відшукання коренів функціонального рівняння x = F (x), і особливо з випадком, коли оператор, що задається функцією F (x), є оператором стиску. На базі розгляду цього методу викладається метод дотичних, що є одним з найбільш розповсюджених методів рішення функціонального рівняння f (x) = 0.
Для читання теорії не потрібно нічого вихідного за рамки програми середньої школи. Деякі припущення з математичного аналізу, що носять допоміжний характер і разом з тим даний самостійний загально-математичний інтерес, приведений з доказами, цілком доступними школярам.
Допоміжні твердження
Доведемо кілька допоміжних тверджень, що мають у курсі математичного аналізу великий самостійний інтерес.
1.Будемо говорити, що визначена в деякій області точка x = x0 функція f(x) зростає у точці x0, якщо існує така досить мала область точки x0, у межах якої f(x) > f (x0) при x > x0, f (x) < f (x0) при x < x0 (відповідно f (x) < f (x0) при x > x0, f (x) > f (x0) при x < x0).
Теорема 1. Якщо функція f (x) має похідну в точці x0 і f '(x0) > 0 (відповідно f'(x0) < 0), то функція f (x) зростає у точці x0.
Для доведення цієї теореми заради визначеності розглянемо випадок f'(x0) > 0 (випадок f '(x0) < 0 розглядається зовсім аналогічно). Тому що похідна f '(x0), по визначенню, дорівнює межі при x > x0 різницевого відношення, де в малій області точки x0 різницеве відношення (1) як завгодно мало відрізняється від f '(x0), і тому що f '(x0) > 0, то в досить малій області точки x0 різницеве відношення (1) додатне. Це означає, що в зазначеній досить малій області цієї точки f (x) - f (x0) > 0 при x – x0 > 0 і f(x)- f (x0) < 0 при x – x0 <0 або, що те ж саме, f (x) > f (x0) при x > x0 і f (x) < f (x0) при x < х0.
Теорема доведена.
2. Будемо говорити, що визначена в деякій області точки x = x0 функція f (x) має в точці x0 локальний максимум (відповідно локальний мінімум), якщо існує така досить мала область точки x0, у межах якої значення f (x0) є найбільшим (відповідно найменшим) серед усіх значень f (x) цієї функції.
Теорема 2. Якщо функція f (x) має похідну в точці x0 і має в цій точці локальний максимум або локальний мінімум, то обов'язково f '(x0) = 0.
Для доведення цієї теореми зазначимо, що функція f (x), що має в точці x0 локальний максимум або локальний мінімум, не може в цій точці x0 ні зростати, ні спадати. Отже, з теореми 1 похідна f '(x0) не може бути ні додатною, ні від’ємною, тобто f '(x0) = 0. Теорема доведена.
3. Нагадаємо, що функція f (x) називається безперервною в даній точці x0, якщо в цієї функції існує в точці x0 границя рівна її значенню f (x0) у цій точці.
Теорема 3 (теорема Ролля). Якщо функція f (x) безперервна в кожній точці відрізка [а;b] і має похідну у всіх внутрішніх точках цього відрізка і якщо, крім того, f (a) = f (b), то усередині цього сегмента найдеться точка x, похідна f '(x) у якій дорівнює нулю.
Будемо спиратися на наступне встановлюване в курсі математичного аналізу твердження, що належить К.Т.В. Вейерштрассу: якщо функція f (x) безперервна в кожній точці відрізка [a;b], то на цьому відрізку знайдеться точка x0, значення функції f(x0) у якій є максимальним серед усіх значень функції f (x) на зазначеному відрізку, і точка x1, значення функції f (x1) у якій є мінімальним серед значень функції f (x) на зазначеному відрізку.
Переходячи до доведення теореми 3, розглянемо спочатку випадок, коли функція f (x) є постійною на відрізку [ a; b], тобто для всіх x з цього відрізка f (x) = f (a) = f (b).
У цьому випадку похідна f '(x) дорівнює нулю в будь-якій точці x сегмента [a;b]. Нехай тепер f (x) не є постійною на відрізку [a;b]. Тоді хоча б в одній внутрішній точці x цього відрізка значення f (x) не дорівнює f (a). Нехай заради визначеності це значення f (x) > f (a). Тоді максимальне значення функції f (x) на даному відрізку досягається в деякій внутрішній точці x цього відрізка і функція f (x) має в цій точці x локальний максимум. За теоремою 2 f '(x) = 0.
Теорема доведена.
4. Теорема 4 (теорема Лагранжа). Якщо функція f (x) безперервна в кожній точці відрізка [a;b] і має похідну у всіх внутрішніх точках цього відрізка, то усередині цього відрізка знайдеться точка x, така, що виконується рівність, названа формулою Лагранжа:
f (b) - f (a) = f '(x)(b - a)
Для доведення цієї теореми розглянемо на відрізку [a;b] допоміжну функцію і помітимо, що для цієї функції виконані на даному відрізку всі умови теореми 3. Дійсно, функція f (x) безперервна на відрізку [a;b] (як різниця безперервної функції f (x) і лінійної функції) і має у внутрішніх точках цього відрізка похідну. З рівності (3) очевидно, що f (a) = f (b) = 0. У силу теореми 3 усередині відрізка [a;b] знайдеться точка x, така, що f (a) = f (b) = f”(x)(b-a)
Теорема доведена.
