Відділ освіти виконкому Тернівської районної у місті ради
Криворізька загальноосвітня школа І-ІІІ ступенів №117
секція: математика
Функціональні рівняння
Та методи їх розв’язання
Науково-дослідницька робота
учениці 11 класу
Криворізької загальноосвітньої
школи І-ІІІ ступенів №42
Воронова Юлія Валентинівна
Науковий керівник
Попова Віолета Олександрівна
вчитель математики
«спеціаліст вищої категорії»,
Кривий Ріг - 2016
Зміст
Вступ. 3
Розділ 1 Аналітичний метод. 5
Розділ 2 Метод підстановок. 8
Розділ 3 Ітераційний метод. 11
Розділ 4 Метод диференціювання. 18
Розділ 5 Метод зверненян до рівняння в скінченних різницях. 20
Висновки. 22
Список використаних джерел. 23
Вступ
Нині немає жодної
галузі людського знання,
куди не входили б поняття
про функцію, їх графічне
зображення та взаємозв’язок.
К. Ф. Лебединцев
Питання про розв’язування функціональних рівнянь – одне з найстаріших у математиці. Приклади таких рівнянь зустрічаються у працях Л. Ейлера, Н. Абеля, К. Гауса, О. Коші, М. Лобачевского, Г. Монжа та інших видатних математиків.
Необхідність вивчення на практиці залежностей між змінними різної природи привели до поняття функції в математиці, а залежність між функціями різних аргументів до функціонального рівняння. Під функціональним рівнянням розуміють рівняння, в яких шукані функції зв’язані з відомими функціями (однієї чи кількох змінних), а допомогою операції утворення складеної функції. Одними з найпростіших функціональних рівнянь є рівняння Коші:
1.  (х+ у)=
(х+ у)=  ;
;
2.  ;
;
3.  ;
;
4.  .
.
Розв’язати дане рівняння означає встановити, чи має воно розв’язки, і знайти їх, якщо вони існують. Процес відшукання розв’язків визначається самим рівнянням, а також умовами, що виражають ті чи інші властивості, які повинна мати шукана функція (неперервність, монотонність, обмеженість, диференційованність тощо). Так, наприклад, неперервними розв’язками наведених вище рівнянь Коші відповідно є функції  ,
,  ,
,
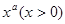 ,
,  .
.
Властивість періодичності означується за допомогою рівняння  Так, наприклад, розв’язком першого рівняння Коші можна вважати функцію у=rx, де r – число, х – змінна. Саме рівняння це, так звана розподільна властивість. Розв’язком другого рівняння Коші буде функція у=ах, де а – число, х – змінна, х>0 (рівняння виражає властивість: добуток степенів з однаковими основами). Розв’язком третього рівняння Коші -
Так, наприклад, розв’язком першого рівняння Коші можна вважати функцію у=rx, де r – число, х – змінна. Саме рівняння це, так звана розподільна властивість. Розв’язком другого рівняння Коші буде функція у=ах, де а – число, х – змінна, х>0 (рівняння виражає властивість: добуток степенів з однаковими основами). Розв’язком третього рівняння Коші - 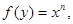 де х – змінна, n – число(піднесення до степеня різних основ).
де х – змінна, n – число(піднесення до степеня різних основ).
4.-  х>0, a>0, a
х>0, a>0, a 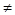 1.
1.
Крім того, в шкільному курсі математики зустрічається функціональне рівняння, розв’язками яких є тригонометричні функції. В цих рівняннях функції пов’язані між собою, так званою, властивістю періодичності  .
.
Розділ 1 Аналітичний метод
Цей метод полягає в тому, що розв'язок функціонального рівняння відшукується поступово для натуральних, цілих, раціональних і дійсних значень аргументу. Він вимагає, як правило, використання умови неперервності функції.
Приклад 1.1. Знайти всі неперервні функції  такі, що для будь-яких х, у виконується рівність
такі, що для будь-яких х, у виконується рівність
 (х+у)=
(х+у)=  (х)+
(х)+  (у). (1.1)
(у). (1.1)
Розв'язання. Поклавши в (1.1) х=у=0, одержимо  . Звідси випливає, що
. Звідси випливає, що 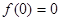 . Підставивши у=-х в (1.1), матимемо
. Підставивши у=-х в (1.1), матимемо

Таким чином,  (х) — непарна функція.
(х) — непарна функція.
Нехай у=х, у=2х, у=3х,..., у=пх, де п — натуральне число. Підставивши ці значення в (1.1), знаходимо  (за індукцією). Отже, для будь-якого натурального п
(за індукцією). Отже, для будь-якого натурального п
 (1.2)
(1.2)
Звідси випливає, що
 (1.3)
(1.3)
Надавши в рівності (1.2) змінній значення 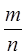 , дістанемо
, дістанемо  для довільних т, п
для довільних т, п  . Врахувавши (1.3), матимемо
. Врахувавши (1.3), матимемо


Нехай х — довільне невід'ємне дійсне число. Тоді існує послідовність  додатних раціональних чисел, яка збігається до х при
додатних раціональних чисел, яка збігається до х при  Оскільки функція
Оскільки функція  неперервна в точці х, то
неперервна в точці х, то  .
.
Таким чином,
 (1.5)
(1.5)
для всіх невід'ємних дійсних х.
Якщо х<0, то (-х)>0. Використавши, що  — непарна функція, дістаємо.
— непарна функція, дістаємо.

Отже, розв'язком рівняння (1.1) є функція виду (1.5), визначена для всіх дійсних х.
Приклад 1.2. Розв'язати в класі неперервних функцій рівняння 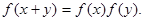 (1.6)
(1.6)
Розв'язання. З (1.6) випливає, що
 при будь-якому
при будь-якому 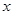 .
.
А це означає, що  набуває лише невід'ємних значень.
набуває лише невід'ємних значень.
Припустимо, існує х0 таке, що  . Тоді для довільного х маємо
. Тоді для довільного х маємо 
Отже, або  (х)=0, або
(х)=0, або  (х)>0 для всіх значень змінної х.
(х)>0 для всіх значень змінної х.
Нехай  (х)>0. Тоді функція
(х)>0. Тоді функція 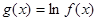 визначена для всіх х і неперервна. Скориставшись (1.6), одержимо
визначена для всіх х і неперервна. Скориставшись (1.6), одержимо  або
або

Використавши результат прикладу 1.1, робимо висновок, що  Звідки
Звідки  , де
, де  >0.
>0.
Приклад 1.3. Знайти функції  , визначені на множині додатних чисел, які задовольняють умовам:
, визначені на множині додатних чисел, які задовольняють умовам:
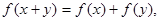 (1.7)
(1.7)
 (1.8)
(1.8)
Розв 'язання. Основною складністю цього прикладу, в порівнянні з попередніми, є відсутність інформації про неперервність функції  , що не дає можливості використати граничний перехід при знаходженні значень функції в ірраціональних точках.
, що не дає можливості використати граничний перехід при знаходженні значень функції в ірраціональних точках.
Підставимо у рівнянні (1.8) у=1.Тоді  Отже, або
Отже, або  (х)=0, або
(х)=0, або  (1)=1. Функція
(1)=1. Функція  (х)=0 є розв'язком системи рівнянь (1.7), (1.8).
(х)=0 є розв'язком системи рівнянь (1.7), (1.8).
Нехай  (1)=1. Поклавши в (1.8) х=у =
(1)=1. Поклавши в (1.8) х=у =  , одержимо
, одержимо  Тобто для всіх додатних х виконується умова
Тобто для всіх додатних х виконується умова
 (1.9)
(1.9)
З рівняння (1.7) маємо, що для всіх додатних раціональних х  , де
, де  (див. приклад 1.1). Оскільки
(див. приклад 1.1). Оскільки 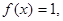 , то для всіх додатних раціональних х виконується умова
, то для всіх додатних раціональних х виконується умова 
Покажемо, що 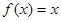 і для всіх дійсних х>0. Припустимо, що існує х0>О таке, що
і для всіх дійсних х>0. Припустимо, що існує х0>О таке, що  . Нехай
. Нехай  <
<  . Виберемо раціональне
. Виберемо раціональне 
 так, щоб
так, щоб  <r<x0. Тоді з (1.7) одержимо, що
<r<x0. Тоді з (1.7) одержимо, що

Оскільки з умови (1.9) випливає, що  то
то  А це суперечить вибору r. Провівши аналогічні міркування, одержимо також суперечність для випадку
А це суперечить вибору r. Провівши аналогічні міркування, одержимо також суперечність для випадку  >x0. Отже, функції
>x0. Отже, функції  і
і 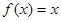 — шукані розв'язки.
— шукані розв'язки.




