Задание№1
Пусть функция имеет следующие значения: f(x, y, z)=(1, 0, 0, 1, 1, 0,1, 1). Найти МДНФ функции методом Куайна.
Решение:
Для данной функции запишем её СДНФ:  .
.
Построим СокрДНФ:
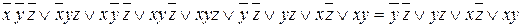

| 
| 
| 
| xyz | |
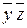
| |||||
| yz | |||||

| |||||
| xy |
Используя сокращённую и совершенную ДНФ построим таблицу Куайна. В верхней строке запишем дизъюнкты совершенной ДНФ, в левом столбце запишем дизъюнкты сокращённой ДНФ. В тех ячейках, где дизъюнктасокращённой ДНФ покрывает дизъюнкту совершенной ДНФ ставим 1. Ввиду наличия единственной единицы в столбцах 1 и 2, конъюнкции 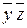 и yz являются ядровыми. Таким образом, единицы ядра находятся в столбцах: 1, 2, 3 и 5. Ни одна из единиц 4–го столбца не покрывается ядром. Тем самым, обе остальные конъюнкции входят в ДНФ Куайна, которая в данном случае совпадает с Сокращенной ДНФ. Для построения МДНФ достаточно иметь одну единицу в 4–ом столбце, это равносильно удалению из СокрДНФ любой из конъюнкций:
и yz являются ядровыми. Таким образом, единицы ядра находятся в столбцах: 1, 2, 3 и 5. Ни одна из единиц 4–го столбца не покрывается ядром. Тем самым, обе остальные конъюнкции входят в ДНФ Куайна, которая в данном случае совпадает с Сокращенной ДНФ. Для построения МДНФ достаточно иметь одну единицу в 4–ом столбце, это равносильно удалению из СокрДНФ любой из конъюнкций:  или xy. При этом получаются две минимальные ДНФ:
или xy. При этом получаются две минимальные ДНФ:  и
и  .
.
Задание №2
Для функции заданной следующим образом f(x,y,z,w)=(1,1,1,1,0,1,0,0,1,0,0,1,1,0,1,1) построить МДНФ с помощью карт Карно.
| z w | |||||

| |||||
| x | |||||
| y | |||||
| Рисунок 1 |
Решение:
Значения функции перечислены в порядке естественного увеличения наборов значений переменных, рассматриваемых как четырехразрядные двоичные числа.
Изобразим карту Карно для данной функции, проставляя в ней только единичные значения.
Разобьем единицы по группам, как показано на рисунке1. Тогда соответствующая этому разбиению
МДНФ1 = 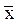
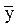 Ú
Ú 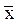
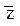 w Ú x
w Ú x 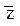
 Ú x z w Ú x y z
Ú x z w Ú x y z
| z w | |||||

| |||||
| x | |||||
| y | |||||
| Рисунок 2 |
Очевидно, что ДНФ той же сложности будет получена, если разбить единицы на группы так, как показано на рис. 2
Соответствующая этому разбиению
МДНФ2 = 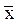
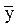 Ú
Ú 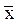
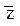 w Ú x
w Ú x 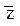
 Ú
Ú 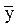 z w Ú x y z
z w Ú x y z
| z w | |||||

| |||||
| x | |||||
 y y
| |||||
| Рисунок 3 |
Для разбиения, показанного на рисунке 3, МДНФ имеет ту же сложность и равна:
МДНФ3 = 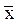
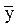 Ú
Ú 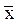
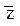 w Ú x
w Ú x 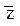
 Ú x z w Ú x y
Ú x z w Ú x y 
| z w | |||||
 00 00
| |||||
| x | |||||
| y | |||||
| Рисунок 4 |
А для рисунка 4
МДНФ4 = 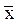
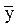 Ú
Ú 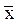
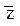 w Ú
w Ú 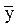
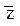
 Ú x z w Ú x y
Ú x z w Ú x y 
Другие варианты разбиения не приведут к более коротким ДНФ. Таким образом для данной функции получено четыре минимальных ДНФ.
Задания для самостоятельного решения:
Задание №1
Пусть дана функция от четырёх переменных f(x, y, z, w). Найти МДНФ функции методом Куайна.
Задание №2
Для функции от четырёх переменных f(x,y,z,w) построить МДНФ с помощью карт Карно.
Варианты заданий:
Вариант №1
1. f(x,y,z)=(0,5,8,9,10,12,13)
2. f(x,y,z)=(0,8,10,11,13,15)
Вариант №2
1. f(x,y,z)=(1,2,3,12,13,14,15)
2. f(x,y,z)=(2,3,7,8,10,11,12,15)
Вариант №3
1. f(x,y,z)=(0,4,6,7,8,10,13,15)
2. f(x,y,z)=(2,3,7,8,10,11,13,15)
Вариант №4
1. f(x,y,z)=(0,4,5,6,7,14,15)
2. f(x,y,z)=(0,3,7,8,9,10,11,12,15)
Вариант №5
1. f(x,y,z)=(2,4,7,9,10,14,15)
2. f(x,y,z)=(0,2,3,5,11,12,15)
Вариант №6
1. f(x,y,z)=(0,2,4,7,8,10,13,15)
2. f(x,y,z)=(3,6,8,9,12,13,15)
Вариант №7
1. f(x,y,z)=(2,4,7,9,10,11,13,15)
2. f(x,y,z)=(0,2,3,4,5,9,10,12)
Вариант №8
1. f(x,y,z)=(5,7,8,9,10,11,15)
2. f(x,y,z)=(2,3,4,9,10,11,14,15)
Вариант №9
1. f(x,y,z)=(0,2,4,8,12,14,15)
2. f(x,y,z)=(2,3,4,6,7,9,11,12)
Вариант №10
1. f(x,y,z)=(5,6,7,8,9,10,11,12,13)
2. f(x,y,z)=(3,5,7,10,11,12,13,14)
Вариант №11
1. f(x,y,z)=(1,2,3,4,9,11,12,14)
2. f(x,y,z)=(3,4,5,6,11,13,15)
Вариант №12
1. f(x,y,z)=(0,1,2,6,10,12,13,14)
2. f(x,y,z)=(2,3,4,8,12,14,15)
Вариант №13
1. f(x,y,z)=(1,2,4,5,9,10,13,14)
2. f(x,y,z)=(0,3,4,6,7,11,12,15)
Вариант №14
1. f(x,y,z)=(0,1,5,6,8,11,12)
2. f(x,y,z)=(2,3,7,8,10,13,14,15)
Вариант №15
1. f(x,y,z)=(1,2,3,4,9,11,12,14)
2. f(x,y,z)=(3,4,6,11,13,15)
Вариант №16
1. f(x,y,z)=(0,2,3,4,10,11,12,15)
2. f(x,y,z)=(3,4,5,9,11,13,15)
Вариант №17
1. f(x,y,z)=(1,2,3,4,7,8,9,11,12,14)
2. f(x,y,z)=(1,2,3,4,6,11,13,15)
Вариант №18
1. f(x,y,z)=(2,3,7,9,11,12,14)
2. f(x,y,z)=(2,4,5,8,11,13,15)
Вариант №19
1. f(x,y,z)=(1,2,3,4,5,11,13,14)
2. f(x,y,z)=(2,4,5,6,7,10,15)
Вариант №20
1. f(x,y,z)=(6,7,8,9,10,14,15)
2. f(x,y,z)=(0,3,5,6,7,11,12,13)
Практическая работа №9
Тема: Основные понятия теории графов.
Задание №1
Дан граф T:

Задать данный граф матрицей смежности и инцидентности.
Решение:
Матрица инцидентности – это прямоугольная матрица, число строк которой равно числу вершин, количество столбцов – числу дуг (рёбер) графа. На пересечении строки и столбца ставится 1, если вершина является началом дуги, -1 – если концом дуги, 0 – если вершина и дуга не инцидентны.
| AB | AG | AF | FE | FG | GB | GM | EG | EM | ED | DC | MC | BC | |
| A | |||||||||||||
| B | -1 | -1 | |||||||||||
| C | -1 | -1 | -1 | ||||||||||
| D | -1 | ||||||||||||
| E | -1 | ||||||||||||
| F | -1 | ||||||||||||
| G | -1 | -1 | -1 | ||||||||||
| M | -1 | -1 |
Матрица смежности – это квадратная матрица, размер которой определяется числом вершин в графе. На пересечении строки и столбца ставится 1, если вершины инцидентны и 0 в противном случае.
| A | B | C | D | E | F | G | M | |
| A | ||||||||
| B | ||||||||
| C | ||||||||
| D | ||||||||
| E | ||||||||
| F | ||||||||
| G | ||||||||
| M |
Задание №2
Для данного графа (см. задание №1) вычислить хроматическое число h(T).
Решение:
- Выделяем вершинно пустые подграфы графа, т.е. подмножества не инцидентных вершин:
E1={F, B, M, D}, E2={A, E, C}, E3={F, C}, E4={A, M, D}, E5={G, D}, E6={G, C},
E6={F, M}, E8={B, E}.
- Строим двумерную таблицу,число строк которой равно числу подграфов, а число столбцов – числу вершин. На пересечении столбца и строки ставим единицу, если вершин содержится в подграфе.
- Определяем покрытие столбцов строками, т.е. в каждом столбце должна быть хотя бы одна единица. Каждое покрытие порождает раскраску. Покрытие минимальной мощности определяет хроматическое число графа.
| A | B | C | D | E | F | G | M | |
| E1 | ||||||||
| E2 | ||||||||
| E3 | ||||||||
| E4 | ||||||||
| E5 | ||||||||
| E6 | ||||||||
| E7 | ||||||||
| E8 |
Минимальное покрытие столбцов строками является множество {E1, E2, E5}. Следовательно, хроматическое число графа h(T)=3
Задания для самостоятельного решения:
Задание №1
Задать данный граф матрицами смежности и инцедентности.
Задание №2
Для данного графа (см. задание №1) вычислить хроматическое число h(T).
Варианты заданий:
Вариант №1

| Вариант №2

|
Вариант №3

| Вариант №4

|
Вариант №5
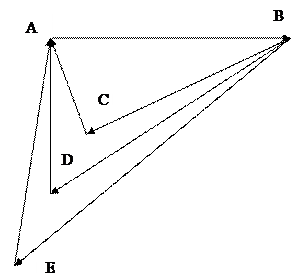
| Вариант №6
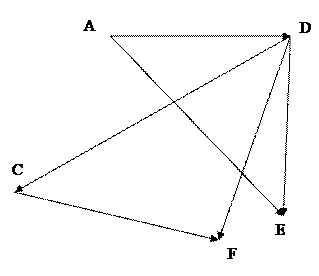
|
Вариант №7

| Вариант №8
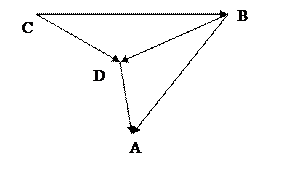
|
Вариант №9

| Вариант №10

| ||||
Вариант №11

| Вариант №12
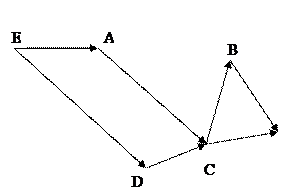
| ||||
Вариант №13

| Вариант №14

| ||||
Вариант №15

| Вариант №16
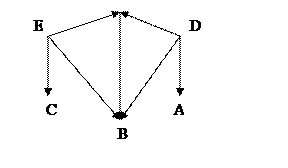
|
Вариант №17

| Вариант №18

| ||
Вариант №19
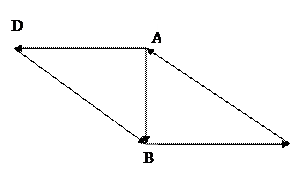
| Вариант№20

|
Практическая работа №10






