 Площадь криволинейной трапеции ограниченной линиями
Площадь криволинейной трапеции ограниченной линиями  ,
, 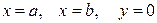 , расположенной выше оси Ох (
, расположенной выше оси Ох (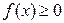 ), равна:
), равна:

 .
.
 Если криволинейная трапеция расположена ниже оси Ох (
Если криволинейная трапеция расположена ниже оси Ох (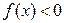 ), то ее площадь может быть найдена по формуле
), то ее площадь может быть найдена по формуле
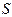
 .
.
 Пусть на отрезке
Пусть на отрезке  заданны и непрерывны функции
заданны и непрерывны функции 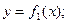
 такие, что
такие, что 
 . Площадь фигуры
. Площадь фигуры  , ограниченной кривыми
, ограниченной кривыми  ,
,  , и прямыми
, и прямыми 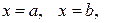 вычисляется по формуле:
вычисляется по формуле:
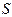
 .
.
 Площадь криволинейной трапеции, верхняя граница которой задана параметрическими уравнениями
Площадь криволинейной трапеции, верхняя граница которой задана параметрическими уравнениями

 , вычисляется по формуле:
, вычисляется по формуле:
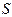
 .
.
 Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением  и двумя полярными радиусами, составляющими с полярной осью углы
и двумя полярными радиусами, составляющими с полярной осью углы  и
и 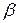 , вычисляется по формуле:
, вычисляется по формуле:
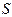
 .
.
Пример 4. Найти площадь плоской фигуры ограниченной линиями
 х=0, у=4.
х=0, у=4.

Решение. Будем иметь  (ед2).
(ед2).
Пример 5. Найти площадь фигуры, ограниченной линиями
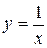 ,
, 
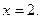
|
 Решение.
Решение.


|

|



Вычисление объёмов тел вращения.
Объём тела, полученного вращением вокруг оси Оx, криволинейной трапеции 
 ,
,  определяется формулой
определяется формулой
 .
.
Пример 6. Найти объем тела, образованного вращением
фигуры, ограниченной линиями  ,
,  ,
,  , х= 1 вокруг оси Оx,
, х= 1 вокруг оси Оx,
 |
Решение.

Ответ:  .
.
Пример 7. Найти объём тела вращения плоской фигуры

а) вокруг оси Ox,
б) вокруг оси Oy.
 Решение.
Решение.
а) Найдем объем тела вращения вокруг оси OX.

Будем иметь  и
и  ,
,

 .
. 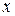
Формулы длин дуг плоских кривых.
 Длина
Длина  кривой, заданной уравнением
кривой, заданной уравнением  ,
,  вычисляется по формуле:
вычисляется по формуле:

 Длина
Длина  кривой заданной параметрическими уравнениями
кривой заданной параметрическими уравнениями

 , вычисляется по формуле:
, вычисляется по формуле:

 Длина
Длина  кривой заданной в полярных координатах уравнением
кривой заданной в полярных координатах уравнением

вычисляется по формуле:
 .
.
Пример 8. Найти длину дуги кривой  от
от  до
до  .
.
Решение. Кривая симметрична относительно оси Ox. Найдем длину верхней ветви кривой. Из уравнения  находим
находим  . По формуле вычисления длины дуги получим
. По формуле вычисления длины дуги получим


Контрольные вопросы.
1.Определённый интеграл
2.Формула Ньютона- Лейбница.
3. Вычисление объёмов тел вращения.
Задания.
1. Вычислить интегралы
1) 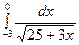 ; 2)
; 2)  3)
3) 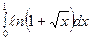 ; 4)
; 4)  ;
;
5)  : 6)
: 6)  .
.
2. Найти площади фигур ограниченных линиями:
1)  ,
,  ,
,  ; 2)
; 2)  , у=1-х2, х=0; 3)
, у=1-х2, х=0; 3) 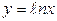 , х=е,у=0.
, х=е,у=0.
3.Найти объём тела, образованного вращением фигуры ограниченной линиями:
 =4-х2; у=0; х=0;
=4-х2; у=0; х=0; 
1) вокруг оси Ox; 2) вокруг оси Oy.
4. Найти длину дуги кривой:
а) 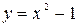 отсеченной осью Ox;
отсеченной осью Ox;
б) 
в) Кардиоиды 
Занятие 10.
Несобственные интегралы.
 Несобственные интегралы первого рода с бесконечными пределами определяются как интегралы вида:
Несобственные интегралы первого рода с бесконечными пределами определяются как интегралы вида:
 ,
,  ,
, 
Если предел существует и конечен, то несобственный интеграл называется сходящимся, если же предел не существует, то интеграл называется расходящимся.
 Если
Если  непрерывна для всех значений отрезка
непрерывна для всех значений отрезка 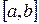 , кроме точки с, в которой
, кроме точки с, в которой  имеет разрыв второго рода, то несобственным интегралом второго рода от неограниченнойфункции
имеет разрыв второго рода, то несобственным интегралом второго рода от неограниченнойфункции  называется интеграл вида:
называется интеграл вида:

 Признак сравнения. Если функции
Признак сравнения. Если функции  и
и  непрерывны на промежутке
непрерывны на промежутке  и удовлетворяют на этом промежутке условию
и удовлетворяют на этом промежутке условию  , то из сходимости интеграла
, то из сходимости интеграла  следует сходимость интеграла
следует сходимость интеграла  , и из расходимости интеграла
, и из расходимости интеграла  следует расходимость интеграла
следует расходимость интеграла  .
.
Пример 1. Исследовать сходимость интеграла 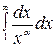 , где
, где  - некоторое число.
- некоторое число.
Решение. 1) Если  , то для любого
, то для любого 

2) Если  , то для любого
, то для любого 
 .
.
Итак, данный интеграл при  сходится, при
сходится, при  расходится и при
расходится и при 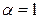 расходится.
расходится.
Пример 2. Исследовать сходимость  .
.
Решение. Сравним подынтегральную функцию  с функцией
с функцией 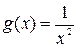 на
на 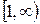 . Очевидно, что
. Очевидно, что
 .
.
Но интеграл 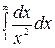 сходится, так как
сходится, так как 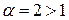 (см. пример 1.) Следовательно, согласно признаку сравнения, сходится и данный ряд.
(см. пример 1.) Следовательно, согласно признаку сравнения, сходится и данный ряд.
Пример 3. Исследовать сходимость  , где
, где  - некоторое число.
- некоторое число.
Решение. 1) Если  , для некоторого
, для некоторого  ,то
,то
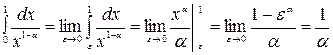
2) Если  , то
, то
 ,
,
3) Если  , для некоторого
, для некоторого  , то
, то
 .
.
Контрольные вопросы.
1. Несобственные интегралы.
2. Признак сравнения.
Задания.
1. Вычислить интегралы
1) 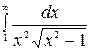 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 

2.Исследовать сходимость интегралов
1)  , 2)
, 2)  3)
3) 
4), 5), 6).
Математический анализ
Типовой расчёт по теме «Предел и производная»
Задача 1. Вычислить 

| № | 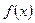
| 
| № | 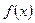
| 
|
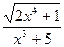
| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
|
Задача 2. Вычислить  , используя второй замечательный предел.
, используя второй замечательный предел.
| № | 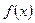
| 
| № | 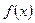
| 
|

| 
| 
| 
| ||

| 
| 
| |||

| 
| ||||

| 
| 
| 
| ||
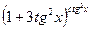
| 
|
Задача 3. Вычислить  с помощью замены бесконечно малых на эквивалентные.
с помощью замены бесконечно малых на эквивалентные.
| № | 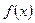
| № | 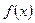
|
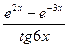
| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задача 4. Найти точки разрыва функции  .
.
Определить характер разрывов.
| № | а | b | с | k | № | а | b | с | k |
| -1 | |||||||||
| -2 | |||||||||
| -2 | |||||||||
| -1 | -1 |
Задача 5. Найти производную функцию 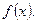
| № | 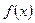
| № | 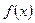
|

| 
| ||
 
| 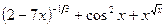
| ||

| 
| ||

| 
| ||

| 
|
Задача 6. Найти производную  функции, заданной
функции, заданной
параметрически:  .
.
| № | 
| 
| № | 
| 
|

| 
| 
| 
| ||

| 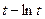
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
|
Задача 7. Найти производную  неявной функции, заданной уравнением
неявной функции, заданной уравнением 
| № | 
| № | 
|

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задача 8. Вычислить с помощью дифференциала приближенное значение числа  .
.
| № | 
|

| |

| |

| |

| |

| |

| |

| |

| |

| |
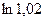
|
Задача 9. Определить, в каких точках заданной линии L касательная к этой линии параллельна прямой  , и написать уравнение этой касательной.
, и написать уравнение этой касательной.
| № | Уравнение линии 
| 
| № | Уравнение линии 
| 
|
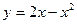
| 
| -2 | |||

| 
| 
| |||

| -1 | 
| 
| ||

| -1 | 
| 
| ||

| -1 | 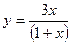
|
Для заметок
Для заметок
Для заметок
Для заметок
Для заметок
Алборова Мира Сослановна
Высшая математика часть 2
Методические указания по практическим занятиям
Подписано к печати:
Тираж:
Заказ №







