При достаточно малых  приращение функции приближенно равно ее дифференциалу, т. е.
приращение функции приближенно равно ее дифференциалу, т. е.  и
и
 .
.
Пример 9. Найти дифференциал функции  .
.
Решение. Найдем производную данной функции  .
.
Следовательно, по определению дифференциала функции получим
 .
.
Пример1 0. Вычислить с помощью дифференциала приближенное значение 
Решение. Рассмотрим функцию  . Пологая
. Пологая  и применяя формулу
и применяя формулу 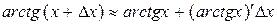 , получим
, получим
 .
.
Производные высших порядков.
Производной второго порядка (второй производной) функции  называется производная от производной
называется производная от производной 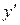 . Вторая производная обозначается так:
. Вторая производная обозначается так: 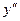 , или
, или  , или
, или 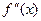 .
.
Если  - закон прямолинейного движения точки, то вторая производная пути по времени
- закон прямолинейного движения точки, то вторая производная пути по времени  есть ускорение этого движения.
есть ускорение этого движения.
Аналогично производная третьего порядка функции  есть производная производной второго порядка
есть производная производной второго порядка  и т.д., производной n -го порядка от функции
и т.д., производной n -го порядка от функции  называется производная от производной
называется производная от производной 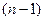 -го порядка
-го порядка 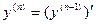 . Обозначается n -я производная так:
. Обозначается n -я производная так:  или
или  , или
, или  .
.
Пример 10. Дана функция  .
.
Найти:  ,
, 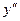 ,
,  ,…
,…
Решение.
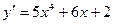 ;
;  ;
;
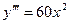 ;
;  ;
; 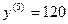 ;
;
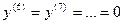 .
.
Пример 11. Дана функция 
Найти: 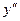 .
.
Решение.  ,
,

Контрольные вопросы.
Производная функции.
2.Основные правила дифференцирования.
3.Производная обратной функции.
4.Формулы дифференцирования основных элементарных функций.
5.Понятия дифференциала функции.
6.Применение дифференциала к приближенным вычислениям.
7.Производные высших порядков.
Задания.
1. Пользуясь определением производной вычислить производные следующих функций:
1)  ;
;
2)  .
.
2. Найти производные и дифференциалы следующих функций
 ;
;  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
 ;
;  .
.
3.Найти производные функций:
1)  ;
;
2)  ;
;
3)  ;
;
4) 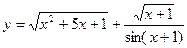 .
.
4.Найти 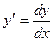 ,
,
1) если  ,
, 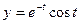 ;
;
2) если  ,
,  ;
;
3) если  ,
,  .
.
5.Вычислить с помощью дифференциала приближенные значения
 ,
,  ,
, 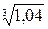 ,
,  .
.
6.Найти производные
1)обратных тригонометрических функций
 ;
; 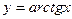 ;
; 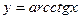 ;
;  ;
;  .
.
2)  обратную к
обратную к  .
.
7. Найти  ,
, 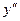 ,
,  ,…,
,…,  для функций:
для функций:
1)  . 2)
. 2)  . 3)
. 3)  . 4)
. 4)  .
.
Занятие 5
1. Теоремы Ролля, Лагранжа, Коши. Фрмула Тейлора.
 Теорема Ролля. Если функция
Теорема Ролля. Если функция 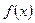 непрерывна на отрезке
непрерывна на отрезке  , дифференцируема в интервале
, дифференцируема в интервале 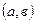 и
и  то в интервале
то в интервале 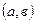 найдётся хотя бы одно значение
найдётся хотя бы одно значение  , при котором
, при котором 
 Теорема Лагранжа (о конечном приращении). Если функция
Теорема Лагранжа (о конечном приращении). Если функция 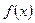 непрерывна на отрезке
непрерывна на отрезке  , дифференцируема в интервале
, дифференцируема в интервале  , то в этом интервале найдётся хотя бы одно значение
, то в этом интервале найдётся хотя бы одно значение  , при котором выполняется равенство
, при котором выполняется равенство  (геометрический смысл: касательная в точке
(геометрический смысл: касательная в точке  параллельна секущей АВ).
параллельна секущей АВ).
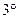 Теорема Коши. Если функции
Теорема Коши. Если функции 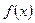 и
и  непрерывны на отрезке
непрерывны на отрезке  и дифференцируемы в интервале
и дифференцируемы в интервале 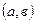 , причём
, причём 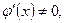 то в этом интервале найдётся хотя бы одно значение
то в этом интервале найдётся хотя бы одно значение  , при котором
, при котором 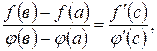 где
где  .
.
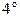 Формула Тейлора. Если функция
Формула Тейлора. Если функция 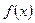 имеет в точке
имеет в точке 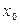 все производные до порядка
все производные до порядка  включительно, то
включительно, то

Это соотношение называется формулой Тейлора с остаточным членом в форме Пеано.
При 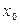 = 0 получаем частный случай формулы Тейлора- формулу Маклорена
= 0 получаем частный случай формулы Тейлора- формулу Маклорена 
Приведем разложение некоторых функций по формуле Маклорена:
 ,
,
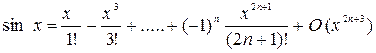 ,
,



Пример 1. Выполняется ли теорема Ролля для функции 
если а=-3; в=3. Найти значение  .
.
Решение. Так как функция  непрерывна и дифференцируема при всех значениях х и её значения на концах отрезка
непрерывна и дифференцируема при всех значениях х и её значения на концах отрезка  равны
равны  Следовательно, условия теоремы Ролля на этом отрезке выполняются. Значение
Следовательно, условия теоремы Ролля на этом отрезке выполняются. Значение  определяем из уравнения
определяем из уравнения  , т.е.
, т.е.  .
.
Пример 2. На дуге АВ кривой  найти точку М, в которой касательная параллельна хорде АВ, если А(1,3) и В(3,3).
найти точку М, в которой касательная параллельна хорде АВ, если А(1,3) и В(3,3).
Решение. Функция  непрерывна и дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями а=1 и в=3 существует значение х=
непрерывна и дифференцируема при всех значениях х. По теореме Лагранжа между двумя значениями а=1 и в=3 существует значение х=  , удовлетворяющее равенству:
, удовлетворяющее равенству:

где 
Подставив соответствующие значения, получим

Отсюда  . Таким образом, точка М имеет координаты М(2;4).
. Таким образом, точка М имеет координаты М(2;4).
Пример 3. Проверить теорему Коши для функции  =х3 и
=х3 и  и найти с.
и найти с.
Решение. Из формулы Коши имеем
 , т.е.
, т.е.  .
.
Отсюда, получим  .
.
Пример 4. Разложить функцию  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  .
.
Решение. Представим, данную функцию в виде
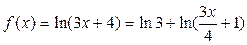 .
.
Далее воспользуемся формулой  .
.
Будем иметь

Пример 5. Вычислить предел, используя разложение по формуле Тейлора
 .
.
Решение. Так как
 и
и  то получим
то получим

Контрольные вопросы.
1. Теоремы Ролля, Лагранжа, Коши.
2.Формула Тейлора. Формула Маклорена.
3.Разложение элементарных функций в ряд Маклорена.
Задания.
1. Применима ли теорема Ролля к функции  на отрезке
на отрезке  . Пояснить графически.
. Пояснить графически.
2. Проверить теорему Лагранжа и найти с для функций: а)  на отрезке
на отрезке 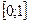
б)  на отрезке
на отрезке 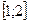
3.Проверить теорему Коши и найти с для функций: а)  и
и 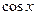 на отрезке
на отрезке 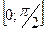 ,
,
б) х2 и  на отрезке
на отрезке  .
.
4. Разложить функцию  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  .
.
5. Найти пределы, используя разложение по формуле Тейлора
а)  ,
,
б)  .
.
Занятие 6.
Правило Лопиталя. (раскрытиенеопределенностей)
Первое правило Лопиталя.
Если функции  и
и  определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки  и при
и при 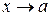
 ,
,  , и производные
, и производные  и
и 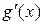 существуют в упомянутой окрестности, за исключением, быть может, самой точки и существует
существуют в упомянутой окрестности, за исключением, быть может, самой точки и существует  ,
,
Тогда
 .
.
Второе правило Лопиталя.
Если функции  и
и  определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки  и при
и при 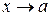
 ,
, 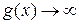 , а производные
, а производные  и
и 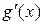 существуют в упомянутой окрестности, за исключением, быть может самой точки и существует
существуют в упомянутой окрестности, за исключением, быть может самой точки и существует  ,
,
Тогда
 .
.
Пример 1. Вычислить предел 
Решение. Применяя первое правило Лопиталя получим  =
=  .
.
Пример 2. Вычислить предел  .
.
Решение. Применяя первое правило Лопиталя получим  .
.
Контрольные вопросы.
1.Первое правило Лопиталя.
2.Второе правило Лопиталя.
Задания.
1.Вычислить пределы, применяя правила Лопиталя:
1) 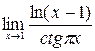 , 2)
, 2)  ,
,
3)  , 4)
, 4)  .
.
Занятие 7.




