Если кривая задана в декартовой системе координат уравнением
, то 
, где 
- угол между касательной к этой кривой в точке с абсциссой 
и положительным направлением оси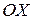 
.
Если кривая задана уравнением , то уравнения касательной и нормали к этой кривой в точке 
имеют соответственно вид:
, (1)
. 
(2)
Угол между двумя кривым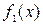и 
и 
в точке их пересечения определяется как угол между прямыми, касательными к этим кривым в точке их пересечения по формуле
, (3)
где 
угловые коэффициенты касательных к кривым в точке их пересечения и равны соответственно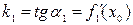 
, 
.
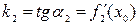Пример 1.Составить уравнение касательной и нормали к кривой в точке.
Решение. Подставляя в заданное уравнение параболы значение 
, находим ординату точки касания 
. Находим угловой коэффициент касательной,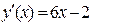 
, следовательно, 
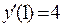. Подставляя найденные значение в уравнение (1), имеем уравнение касательной 
, подставляя эти же значения в уравнение (2), получим уравнение нормали 
.
Пример 2.Найти углы под которыми пересекаются прямая и парабола.
Решение. Найдем точки пересечения кривых, решив систему уравнений 
Отсюда имеем 
, 
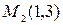. Далее, определим угловые коэффициенты касательных к параболе в точках 
и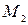 
.Соответственно имеем 
, 
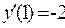. Угловой коэффициент прямой во всех точках один и тот же и равен в нашем случае 2. Далее находим углы 
,
.
Пример 3. Определить в каких точках заданной линии 
касательная к этой линии параллельна прямой 
и написать уравнение этой касательной
, 
.
Решение. Находим производную 
. Далее находим значение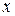 
из уравнения 
. Имеем, 
.Значения функции 
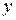при есть 
и 
. Отсюда имеем, 
и 
точки заданной линии в которых касательная к этой линии параллельна данной прямой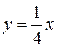 
. Найдем теперь уравнения этих касательных. Используя формулу (1), получим
-уравнение касательной в точке ,
-уравнение касательной в точке .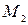
Контрольные вопросы.
1.Геометрический смысл производной.
2.Касательная и нормаль к кривой.
3.Угол между двумя кривыми.
4.Другие приложения производной.
Задания.
1.Найти углы, под которыми пересекаются эллипс и парабола
, 
.
2. Определить в каких точках заданной линии касательная к этой линии параллельна прямой и написать уравнение этой касательной
1) 
, 
; 2) 
, 
; 3) 
, 
.
3.Найти угол между кривой 
и прямой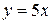 
Занятие 8.
Интегральное исчисление.
Неопределенный интеграл.
Функция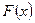 
- называется первообразной для функции 
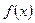на промежутке 
, если в каждой точке этого промежутка выполняется равенство
или 
.
Если 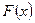первообразная для функции 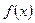, то множество 
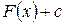, где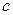 
произвольная постоянная, называется неопределённым интегралом от функции 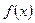и обознается
=
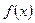
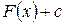
При этом 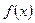называется подынтегральной функцией.
Процесс отыскания первообразной называется интегрированием.
Свойства неопределённого интеграла:
1. 
,
2. 
,
3. 
,
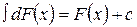4. 
, где некоторая постоянная,
5..
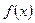
6. (Инвариантность формулы интегрирования) Есл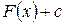и = ,то и
= 
.
Пример 1. Найти первообразную функции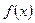 
.
Решение. Рассмотрим функцию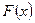 
=> 
.
Следовательно, первообразная есть
.
Таблица основных интегралов:
1. 
,
2. 
при 
,
3. 
,
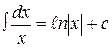4. 
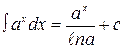, при 
и 
, и в частности 
,
5. 
,
6. 
,
7. 
,
8. 
,
9. 
,
10. 
,
11. 
,
12..
Пример 2. Вычислить интеграл 
.
Решение.
.
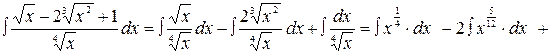
Пример 3. Вычислить интеграл 
.
Решение.
.
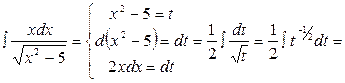
