Пусть  - некоторая постоянная,
- некоторая постоянная,  ,
,  - функции, имеющие производные.
- функции, имеющие производные.
Справедливы следующие правила дифференцирования:
1.  ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ;
;
5.;.
6. Производная сложной функции.
Если функции  и
и  имеют конечные производные, то
имеют конечные производные, то

7. Дифференцирование функции, заданной параметрически..
Пусть зависимость между 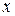 и функцией
и функцией 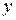 задана параметрически в виде двух уравнений
задана параметрически в виде двух уравнений

где  -вспомогательная переменная, называемая параметром.
-вспомогательная переменная, называемая параметром.
Производная  функции, заданной параметрически определяется по правилу
функции, заданной параметрически определяется по правилу
Или.
8. Производная обратной функции.
Пусть функция  в некоторой окрестности точки
в некоторой окрестности точки  возрастает (или убывает) и является непрерывной. Пусть кроме того, функция
возрастает (или убывает) и является непрерывной. Пусть кроме того, функция  дифференцируема, в точке
дифференцируема, в точке  и производная
и производная  отлична от нуля. Тогда обратная функция
отлична от нуля. Тогда обратная функция 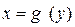 определена в некоторой окрестности соответствующей точки
определена в некоторой окрестности соответствующей точки 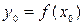 , дифференцируема в этой точке и имеет в этой точке производную, равную
, дифференцируема в этой точке и имеет в этой точке производную, равную  .
.
9. Производная функции  ,
,  , где
, где  и
и  суть функции от
суть функции от 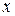 , имеющие в данной точке производные
, имеющие в данной точке производные  и
и  есть:
есть:

Пример 1. Исходя из определения производной, найти производную функции  .
.
Решение. Зададим приращение  , такое, что
, такое, что  .
.
Тогда
 ;
;
Поэтому
 ;
;
Переходим к пределу при  :
:
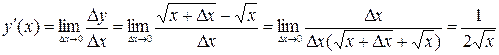 ;
;
т.е.  .
.
Пример 2. Исходя из определения производной функции, найти производную функции  .
.
Решение. Находим

Откуда
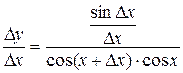
и, следовательно
 .
.
Итак,  .
.
 . Формулы дифференцирования основных элементарных функций:
. Формулы дифференцирования основных элементарных функций:
1.  ; 11.
; 11.  ;
;
2.  ; 12.
; 12.  ;
;
3.  ; 13.
; 13. 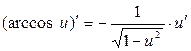 ;
;
4.  ; 14.
; 14.  ;
;
5.  ; 15.
; 15. 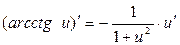 ;
;
6.  ; 16.
; 16.  ;
;
7.  ; 17.
; 17.  ;
;
8.  ; 18.
; 18. 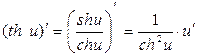 ;
;
9.; 19..
10.  ;
;
Пример 3. Найти производную функции  .
.
Решение.
 .
.
Пример 4. Найти производную  .
.
Решение. Берем производную от  как сложной функции
как сложной функции
 , где
, где  ,
,  .
.
 , где
, где  ,
,
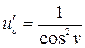 ;
; 
Итак,
 .
.
Пример 5. Найти производную функции 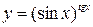
Решение. Имеем  , откуда
, откуда
 ,
,
 .
.
Пример 6. Найти 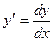 , если
, если  ,
,  .
.
Решение. Имеем

Пример 7. Найти производную  .
.
Решение. Показательная функция  , определена на бесконечной прямой и служит обратной для логарифмической функции
, определена на бесконечной прямой и служит обратной для логарифмической функции  .
.
Согласно вышеуказанному утверждению, функция  дифференцируема в любой точке
дифференцируема в любой точке  и для ее производной справедлива формула
и для ее производной справедлива формула  .
.
Итак, 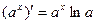 .
.
Пример 8. Вычислить производную  .
.
Решение. Функция  , определенная на интервале
, определенная на интервале  , служит обратной для функции
, служит обратной для функции  , определенной на интервале
, определенной на интервале  . Пользуясь правилом дифференцирования обратной функции, получим:
. Пользуясь правилом дифференцирования обратной функции, получим:
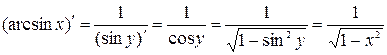 .
.
Мы взяли перед корнем знак +, т.к.  положителен всюду на интервале
положителен всюду на интервале  .
.
Итак  .
.
Понятие дифференциала.
 Пусть функция
Пусть функция  имеет в точке
имеет в точке  конечную производную
конечную производную  , тогда ее приращение можно записать в виде
, тогда ее приращение можно записать в виде
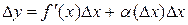 ,
,
где 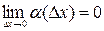 .
.
Главная, линейная относительно  часть
часть  приращения функции называется дифференциалом функции и обозначается
приращения функции называется дифференциалом функции и обозначается  :
:
.
При  , получим
, получим  , поэтому дифференциал функции
, поэтому дифференциал функции  примет вид
примет вид
.
Основные свойства дифференциала
1) 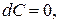 где
где 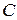 = const,
= const,
2) 
3)  ,
,
4)  ,
,
5) 
6).






