
A) 
B) 4
2. 
A) 
B) 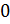
C) ln1
3. 
A) 
4. 
A) 
B) 
5. Дифференциалдаудың ережелері мына теңдіктермен беріледі:
A) 
B) 
6. 
A) [-9, 9]
7. 
A)α = 1 болса, онда қатар жинақсыз
B) α<1 болса, онда қатар жинақсыз
8. 
A) 
9. 
A) 
B) 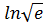
10.  функциясының туындысы:
функциясының туындысы:
B) 
D) 
E) 
11. 
B) [4, 6]
D) (-∞, 2]
E) (-5, -1)
12. 
D) (-3, -1)
E) [-3, 0]
G) (-∞, 4]
13. 
A) (5, +∞) – өсу аралығы
D) (-∞, 5) – кему аралығы
14. 
C) 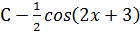
15. 
A) 
D) 
E) 
16. 
A) (-∞, 2]
B) (-1, 1)
17. 
A) (-5, 3)
B) (-1, 1)
18.  функциясының
функциясының  екінші ретті дербес туындысының M0(1;1) нүктесіндегі мәні мына аралықта жатады:
екінші ретті дербес туындысының M0(1;1) нүктесіндегі мәні мына аралықта жатады:
C) (-1, 1)
D) (-∞, 2]
E) (-5, 3)
19.  функциясы үшін дұрыс қатынастар:
функциясы үшін дұрыс қатынастар:
A) 
D) 
G) 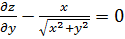
20. 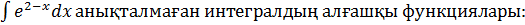
B) 
E) 
21. y = x3 , x = 1, y = 0сызықтарымен қоршалған жазық фигураның ауданына тең сан мына аралықта жатады:
B) 0≤S<2
22.  табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A) (1, 4)
E) (-∞, 4]
G) [1, 4]
23.  шегітең болатын сан:
шегітең болатын сан:
B) e2
E) 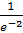
F) e2 * lne
24.  Коши есебінің шешімі:
Коши есебінің шешімі:
A) 
C) 
F) 
25.  теңдеуінің шешімі:
теңдеуінің шешімі:
D) 
E) 
F) 
 Анықталмаған интеграл үшін дұрыс формулалар:
Анықталмаған интеграл үшін дұрыс формулалар:
C) 
D) 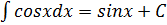
2. 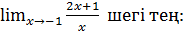
D) 
3. Егер  және
және  шектері бар болса, онда мына теңдіктер орынды болады:
шектері бар болса, онда мына теңдіктер орынды болады:
B) 
C) 
D) 
4.  функциясының туындысы:
функциясының туындысы:
C) 
5.  функциясының туындысы:
функциясының туындысы:
C) 
F) 
6. 
D) (-∞, 4]
E) [-4, 4]
7. 
D) 
E) 
F) 
8. 
A) 
B) 
9. 
C) 
E) 
F) 3
10.  шегі неге тең:
шегі неге тең:
B) 
D) (5)0
F) lne
11. 
C) (-∞, 4]
D) (0, 2]
13.  функциясының туындысы:
функциясының туындысы:
A) 
14.  анықталмаған интегралдың алғашқы функциялары:
анықталмаған интегралдың алғашқы функциялары:
B) 
C) 
15.  анықталмаған интегралдың алғашқы функциялары:
анықталмаған интегралдың алғашқы функциялары:
A) 
16.  анықталған интегралдың мәні жатқан аралықтар:
анықталған интегралдың мәні жатқан аралықтар:
A) (-∞, 2]
B) (-5, 3)
C) (-1, 1)
17. 
B) (-5, 8)
C) (-∞, 3]
F) (-3, 3)
18.  функциясының
функциясының  дербес туындысының M0(1;1) нүктесіндегі мәні мына аралықта жатады:
дербес туындысының M0(1;1) нүктесіндегі мәні мына аралықта жатады:
C) (-4, 4)
F) (-5, 5)
G) (-∞, 4]
19.  функциясының
функциясының  екінші ретті дербес туындысының M0(1;1) нүктесіндегі мәні мына аралықта жатады:
екінші ретті дербес туындысының M0(1;1) нүктесіндегі мәні мына аралықта жатады:
C) (-25, 25)
F) (-30, 30)
20.  табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A) (-∞, 4]
D) [-4, 4]
E) (-4, 4)
21.  шегі тең болатын сан:
шегі тең болатын сан:
A) 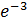
C) 
22.  шегі тең:
шегі тең:
C) e2
E) e2*lne
F) 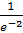
23.  шегітең:
шегітең:
B) 
E) 
24.  Коши есебінің шешімі:
Коши есебінің шешімі:
B) 
25.  теңдеуінің шешімі:
теңдеуінің шешімі:
A) 
G) 
1.Анықталмаған интеграл үшін дұрыс формулалар:
A. 
B. 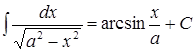 ,
, 
2.  шегі тең болатын сан:
шегі тең болатын сан:
A. 
B. 0
3.  шегі тең:
шегі тең:
A. 
B. 
C. -4
4.  функциясының туындысы:
функциясының туындысы:
A. 
B. 
C. 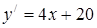
5. Дифференциалдаудың дұрыс ережелері:
A. 
B. 
6.  интегралының мәні мына аралықта жатады:
интегралының мәні мына аралықта жатады:
A. 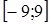
B. 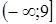
C. 
7.  қатарының жалпы мүшесі:
қатарының жалпы мүшесі:
A. 
B. 
C. 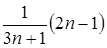
8.  қатарының жалпы мүшесі:
қатарының жалпы мүшесі:
A. 
9.  шегі тең:
шегі тең:
A. 1
B. 
10.  табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A. 
B. 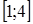
C. 
11.  табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A. 
B. 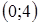
12.  шегі тең болатын сан:
шегі тең болатын сан:
A. 
B. 
13.  функциясы үшін мына тұжырым дұрыс:
функциясы үшін мына тұжырым дұрыс:
A.  минимум нүктесі
минимум нүктесі
14. 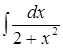 анықталмаған интеграл үшін алғашқы функциялары:
анықталмаған интеграл үшін алғашқы функциялары:
A. 
B. 
C. 
15. 
A. 
B. 
16. 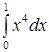 анықталған интегралдың мәні жатқан аралықтар:
анықталған интегралдың мәні жатқан аралықтар:
A. 
B. 
C. 
17.  анықталған интегралдың мәні жатқан аралықтар:
анықталған интегралдың мәні жатқан аралықтар:
A. 
B. 
C. 
18.  функциясы үшін дұрыс табылған дербес туындылар.
функциясы үшін дұрыс табылған дербес туындылар.
A. 
B. 
19.  функциясы үшін дұрыс табылған қатынастар.
функциясы үшін дұрыс табылған қатынастар.
A. 
B. 
C. 
20. 
 табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A. 
B. 
21.  шегі тең болатын сан:
шегі тең болатын сан:
A. 
22.  шегі тең болатын сан:
шегі тең болатын сан:
A. 
23.  шегі тең
шегі тең
A. 
B. 3
C. 
24.  ,
,  Коши есебінің шешімі:
Коши есебінің шешімі:
A. 
25.  теңдеуінің шешімі:
теңдеуінің шешімі:
A. 
1.  шегі тең:
шегі тең:
A. 4
B. 
2. Егер  және
және  шектері бар болса, онда мына теңдіктер орынды болады:
шектері бар болса, онда мына теңдіктер орынды болады:
A. 
B. 
3.  шегі тең:
шегі тең:
A. 
4.  функциясының туындысы:
функциясының туындысы:
A. 
5.  функциясының туындысы:
функциясының туындысы:


6.  интегралының мәні мына аралықта жатады:
интегралының мәні мына аралықта жатады:
A. 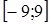
B. 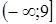
C. 
7.  қатарының жалпы мүшесі:
қатарының жалпы мүшесі:
A. 
B. 
8.  сандық қатары үшін мына тұжырым дұрыс болады:
сандық қатары үшін мына тұжырым дұрыс болады:
A.  болса, онда қатар жинақсыз
болса, онда қатар жинақсыз
B.  болса, онда қатар жинақты
болса, онда қатар жинақты
9.  шегі тең болатын сан:
шегі тең болатын сан:
A. 
B. 1/2
10.  функциясының туындысы:
функциясының туындысы:
A. 
B. 
11.  шегі тең болатын сан:
шегі тең болатын сан:
A. 
B. 3
12.  функциясы үшін
функциясы үшін  және
және  нүктелері:
нүктелері:
A. ІІ текті үзіліс нүктелері
B. Функция анықталмайтын нүктелер
13.  функциясының туындысы:
функциясының туындысы:
A. 
14.  анықталмаған интеграл үшін алғашқы функциялары:
анықталмаған интеграл үшін алғашқы функциялары:
A. 
B. 
C. 
15. 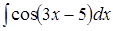 анықталмаған интеграл мына функция болады:
анықталмаған интеграл мына функция болады:
A. 
B. 
16.  анықталған интегралдың мәні жатқан аралықтар:
анықталған интегралдың мәні жатқан аралықтар:
A. 
B. 
C. 
17.  анықталған интегралдың мәні жатқан аралықтар:
анықталған интегралдың мәні жатқан аралықтар:
A. 
B. 
C. 
19. Егер  болса, онда
болса, онда  нүктесіндегі
нүктесіндегі  мәні мына аралықта жатады:
мәні мына аралықта жатады:
A. 
B. 
C. 
20.  анықталмаған интегралдың алғашқы функциялары:
анықталмаған интегралдың алғашқы функциялары:
A.
B. 
C. 
21.  сызықтарымен шенелген жазық фигураның ауданына тең сан мына акралықта жатады:
сызықтарымен шенелген жазық фигураның ауданына тең сан мына акралықта жатады:
A. 
B. 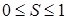
22.  табылған шектің жатқан аралығы:
табылған шектің жатқан аралығы:
A. 
B. 
C. 
23.  шегі тең:
шегі тең:
A. 5/0
B. 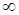
24.  ,
,  Коши есебінің шешімі:
Коши есебінің шешімі:
A. 
B. 
C. 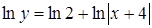
25.  теңдеуінің шешімі:
теңдеуінің шешімі:
A. 
1.  пределом является следующее число:
пределом является следующее число:
C. 
2. Если пределы  и
и  существуют и конечны, то имеют место равенства:
существуют и конечны, то имеют место равенства:
C. 
D. 
E. 
3.  пределом является следующее число:
пределом является следующее число:
A. 
E. 
4. 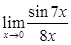 равен:
равен:
D. 
E. 
F. 
5.  производной этой функции является:
производной этой функции является:
C. 
E. 
F. 
6.  производной этой функции является:
производной этой функции является:
A. 
7.Если  и
и  дифференцируемые функции, то справедливо:
дифференцируемые функции, то справедливо:
A. 
D. 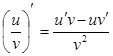
8.Верные формулы дифференцирования:
B. 
9.  равен:
равен:
B. 1
C. 
E. 
10.  равен:
равен:
B. 
C. 
D. 
11.  равен:
равен:
B. 3
C. 
12.Для функции  верные высказывания:
верные высказывания:
C.  - точка максимума
- точка максимума
E.  - интервал возрастания
- интервал возрастания
G. 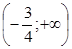 - интервал убывания
- интервал убывания
13.  равен:
равен:
D. 
E. 
G. 
14.  равен:
равен:
A. 
C. 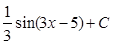
15. 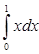 вычисленное значение определенного интеграла лежит в промежутке:
вычисленное значение определенного интеграла лежит в промежутке:
C. 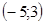
16. 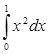 вычисленное значение определенного интеграла лежит в промежутке:
вычисленное значение определенного интеграла лежит в промежутке:
D. 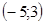
E. 
17.Полным дифференциалом функции  является:
является:
B. 
C. 
18.Для функции  справедливы соотношения:
справедливы соотношения:
D. 
19.  общим решением уравнения являются функции:
общим решением уравнения являются функции:
A. 
20.  найденное значение лежит в промежутке:
найденное значение лежит в промежутке:
C. 
D. 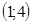
G. 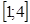
21.  значение лежит в промежутке:
значение лежит в промежутке:
A. 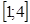
B. 
G. 
22.  сумма корней характеристического уравнения лежит в промежутке:
сумма корней характеристического уравнения лежит в промежутке:
B. 
D. 
E. 
23. Числовое значение площади фигуры, ограниченной линиями  ,
,  ,
,  удовлетворяет неравенству:
удовлетворяет неравенству:
A. 0≤  <5
<5
B.  ≤
≤  ≤5
≤5
24.  сумма ряда лежит в промежутке:
сумма ряда лежит в промежутке:
B. 
C. 
25. Необходимый признак сходимости невыполнен для рядов:
B. 
E. 
1.  пределом является следующее число:
пределом является следующее число:
C. 
F. 0
2.Если пределы  и
и  существуют и конечны, то имеют место равенства:
существуют и конечны, то имеют место равенства:
B. 
C. 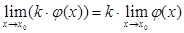
E. 
3.  пределом является следующее число:
пределом является следующее число:
B. 
4. 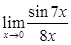 равен:
равен:
C. 
E. 
G. 
5.Если  и
и  дифференцируемые функции и С - постоянная, то:
дифференцируемые функции и С - постоянная, то:
E. 
F. 
G. 
6.  производной этой функции является:
производной этой функции является:
A. 
C. 
E. 
7.Верные формулы дифференцирования:
A. 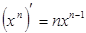
C. 
F. 
8.  производной этой функции является:
производной этой функции является:
C. 
D. 
9.  равен:
равен:
D. 
10. Предел равен 3:
A. 
D. 
11.  равен:
равен:
D. 
F. 
G. 1
12.Для функции  верные высказывания:
верные высказывания:
A. 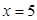 - точка минимума
- точка минимума
C.  - интервал возрастания
- интервал возрастания
13.  равен:
равен:
A. 
B. 
E. 
14.  равен:
равен:
B. 
C. 
E. 
15.  вычисленное значение определенного интеграла лежит в промежутке:
вычисленное значение определенного интеграла лежит в промежутке:
A. 
D. 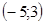
E. 
16.  вычисленное значение определенного интеграла лежит в промежутке:
вычисленное значение определенного интеграла лежит в промежутке:
C. 
D. 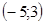
17.Для функции  справедливы соотношения:
справедливы соотношения:
B. 
F. 
18.  - частная производная функции
- частная производная функции  в точке
в точке  лежит в промежутке:
лежит в промежутке:
D. 
E. 
19.  общим решением уравнения являются функции:
общим решением уравнения являются функции:
C. 
D. 
20.  найденное значение лежит в промежутке:
найденное значение лежит в промежутке:
C. 
E. 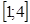
21. Для функции  точки
точки 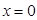 и
и  :
:
C. являются точками разрыва
D. точки разрыва II рода
22.  общим решением уравнения являются функции:
общим решением уравнения являются функции:
B. 
D. 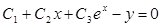
23. Числовое значение площади фигуры, ограниченной линиями  ,
,  ,
,  удовлетворяет неравенству:
удовлетворяет неравенству:
A.  ≤
≤  ≤50≤
≤50≤  <5
<5
24. Необходимый признак сходимости невыполнен для рядов:
A. 
25.  сумма ряда лежит в промежутке:
сумма ряда лежит в промежутке:
A. 
Математический анализ
1.Если пределы  и
и  существуют и конечны, то имеют место равенства:
существуют и конечны, то имеют место равенства:
C. 
1.  равен:
равен:
D. 2
E. 
3.  равен:
равен:
A. 
D. 
E. 
4. Замечательными пределами являются:
D. 
E. 
F. 
5.Верные формулы дифференцирования:
E. 
6.  производной этой функции является:
производной этой функции является:
D. 
E. 
F. 
7.Верные формулы дифференцирования:
A. 
E. 
8.  значение интеграла лежит в промежутке:
значение интеграла лежит в промежутке:
A. 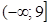
C. 
G. 
9.  равен:
равен:
C. 
D. 3
10.  равен:
равен:
B. 3
11.  пределом является следующее число:
пределом является следующее число:
D. 0
E. 
G. 
12.  равен:
равен:
C. 
E. 
F. 
13. Для функции  верные высказывания:
верные высказывания:
A.  - интервал убывания
- интервал убывания
D.  - точка максимума
- точка максимума
F.  - интервал возрастания
- интервал возрастания
14.  равен:
равен:
E. 
F. 
15.  равен:
равен:
B. 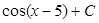
C. 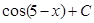
E. 
16.  вычисленное значение определенного интеграла лежит в промежутке:
вычисленное значение определенного интеграла лежит в промежутке:
C. 
D. 
E. 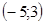
17. 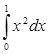 вычисленное значение определенного интеграла лежит в промежутке:
вычисленное значение определенного интеграла лежит в промежутке:
C. 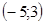
E. 
18.  - частная производная функции
- частная производная функции  в точке
в точке  лежит в промежутке:
лежит в промежутке:
B. 
D. 
19.  - смешанная производная второго порядка функции
- смешанная производная второго порядка функции  в точке
в точке  находится в интервале:
находится в интервале:
B. 
E. 
20.  найденное значение лежит в промежутке:
найденное значение лежит в промежутке:
A. 
F. 
21.  значение лежит в промежутке:
значение лежит в промежутке:
A. 
C. 
22.  решением задачи Коши являются функции:
решением задачи Коши являются функции:
A. 
C. 
23.  - наибольший корень характеристического уравнения лежит в промежутке:
- наибольший корень характеристического уравнения лежит в промежутке:
F. 
G. 
24. Эти ряды условно сходятся:
A. 
1.Если пределы  и
и  существуют и конечны, то имеют место равенства:
существуют и конечны, то имеют место равенства:
B) 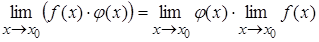
C) 
2. Замечательными пределами являются:
E) 
3.  равен:
равен:
A) 
E) 2
4.  равен:
равен:
E) 
F) 
5. Верные формулы дифференцирования:
A) 
6.  производной этой функции является:
производной этой функции является:
A) 
C) 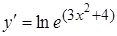
7. Верные формулы дифференцирования:
B) 
E) 
F) 
8.  значение интеграла лежит в промежутке:
значение интеграла лежит в промежутке:
D) ( ,9]
,9]
E) (-9,9)
9.  равен:
равен:
A) 3
C) 
F) 
10. 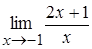 равен:
равен:
C) 
11.  равен:
равен:
A) 
F) -4
G) 
12.  пределом является следующее число:
пределом является следующее число:
D) 0
13.Для функции  верные высказывания:
верные высказывания:
C)  - интервал возрастания
- интервал возрастания
E)  - точка минимума
- точка минимума
G)  - интервал убывания
- интервал убывания
14.  равен:
равен:
C) 
15.  равен:
равен:
A) 
16.  вычисленное значение определенного интеграла лежит в промежутке:
вычисленное значение определенного интеграла лежит в промежутке:
B) 
E) 
G) 
17.






