Таблица 1. Основные единицы СИ
| Величина | Единица измерения | Сокращенное обозначение единицы | |
| русское | международное | ||
| Длина | метр | м | m |
| Масса | килограмм | кг | kg |
| Время | секунда | с | s |
| Сила электрического тока | ампер | А | А |
| Термодинамическая температура | кельвин | К | К |
| Сила света | кандела | кд | cd |
| Количество вещества | моль | моль | mol |
Метр равен длине пути, проходимого светом в вакууме за 1/299792458 долю секунды.
Килограмм равен массе международного прототипа килограмма, который хранится в Международном бюро мер и весов.
Секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную 0,000000020 Н.
Кельвин равен 1/273.16 части термодинамической температуры тройной точки воды.
Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0.012 кг. В одном моле любого вещества содержится число молекул или атомов равное числу Авогадро.
Кандела равна силе света, испускаемого в заданном направлении источником монохроматического излучения частотой 540˙1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср. До 1970 г. кандела называлась свечой.
Международная система единиц включает в себя две дополнительные единицы - для измерения плоского и телесного углов.
Радиан (рад) - угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении радиан равен 57°17'48".
Стерадиан (ср), принимаемый за единицу телесного угла, - телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы.
Производные единицы Международной системы единиц образуются из сочетания основных единиц с помощью простейших уравнений между величинами, в которых числовые коэффициенты равны единице.
Путем добавления к основным единицам установленных приставок образуются кратные (например - километр) или дольные (например - микрометр) единицы. Обозначения кратных и дольных единиц физических величин приведены в таблице 2.
Таблица 2. Обозначения кратных и дольных единиц физических величин
| Множитель | Наименование | Обозначение | |
| Русское | Международное | ||
| 1024 | йота | И | Y |
| 1021 | зета | З | Z |
| 1018 | экса | Э | E |
| 1015 | пета | П | P |
| 1012 | тера | Т | T |
Продолжение табл.2
| Множитель | Наименование | Обозначение | |
| Русское | Международное | ||
| 109 | гига | Г | G |
| 106 | мега | М | M |
| 103 | кило | к | k |
| 102 | гекто | г | h |
| 101 | дека | да | da |
| 10-1 | деци | д | d |
| 10-2 | санти | с | c |
| 10-3 | милли | м | m |
| 10-6 | микро | мк | µ |
| 10-9 | нано | н | n |
| 10-12 | пико | п | p |
| 10-15 | фемто | ф | f |
| 10-18 | атто | а | a |
| 10-21 | зепто | з | z |
| 10-24 | йокто | и | y |
1.7. Понятие погрешности
В процессе развития метрологии сложилось понятие истинного значения физической величины.
Истинное значение физической величины - это значение, которое идеальным образом в качественном и количественном отношениях отражает соответствующее свойство объекта измерений. В практике измерений стремятся получить именно истинные значения физических величин. Однако, добиться этого невозможно из-за несовершенства процедуры измерений.
Процедура измерений состоит из следующих этапов:
1. Выбор объекта исследования (или его модели) и величины, подлежащей измерению;
2. Выбор метода измерений;
3. Выбор средств измерений;
4. Проведение измерительного эксперимента для получения численного значения физической величины.
Всем указанным этапам процедуры измерений присущи различного рода недостатки. Совокупное действие этих недостатков приводит к тому, что результат измерений всегда отличается от истинного значения.
Измеренное значение физической величины (результат измерений) - это значение, полученное при измерении с применением конкретных методов и средств измерений.
Отклонение результата измерений от истинного значения физической величины получило название погрешности измерений:
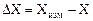, (1.3)
где XИЗМ - измеренное значение; X - истинное значение, ΔX - погрешность измерений.
Поскольку истинное значение физической величины узнать невозможно, в метрологии было введено понятие действительного значения физической величины.
Действительное значение физической величины - это значение, найденное экспериментальным путем и настолько приближающееся к истинному, что для данной цели может быть использовано вместо него. С учетом этого, погрешность измерений можно определить так:
, (1.4)
где XИЗМ - измеренное значение; XД - действительное значение, ΔX - погрешность измерений.
1.8. Формы выражения погрешности
Существуют три формы выражения погрешности: абсолютная, относительная и приведенная.
Абсолютная погрешность - это разность между измеренным (XИЗМ) и действительным (XД) значением физической величины:
. (1.5)
Абсолютная погрешность выражается в единицах измеряемой величины.
Относительная погрешность - это отношение абсолютной погрешности (ΔX) и действительного значения измеряемой величины (XД), выраженное в процентах:
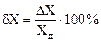. (1.6)
Приведенная погрешность - это отношение абсолютной погрешности (ΔX) и нормированного значения измеряемой величины (XN), выраженное в процентах:
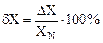(1.7)
За нормированное значение измеряемой величины обычно принимают диапазон измерения прибора:
XN = XК - XН, (1.8)
где XК и XН - соответственно конечное и начальное значение шкалы прибора.
1.9. Классификация погрешности измерений
По источнику возникновения погрешность подразделяется:
1. Инструментальную;
2. Методическую;
3. Субъективную.
Инструментальная погрешность - составляющая погрешности измерений, обусловленная несовершенством применяемых средств измерений. Эта погрешность возрастает по мере эксплуатации средства измерений за счет старения материалов и изменения их характеристик, износа трущихся деталей, и т.д.
Методическая погрешность - составляющая погрешности измерений, возникающая из-за несовершенства используемого метода измерений. Несовершенство метода может быть обусловлено недостаточным теоретическим обоснованием явления или эффекта, положенного в основу метода измерений, использованием упрощенных зависимостей при проведении расчетов и т.д.
Субъективная погрешность - составляющая погрешности измерений, обусловленная участием человека в процессе измерений. Человек является своеобразным звеном в измерительной системе и также обладает метрологическими характеристиками. Метрологические характеристики человека - оператора в основном зависят от двух факторов: условий, в которых человек производит измерения, и его физического состояния (утомленность, невнимательность и т.п.).
Таким образом, математическую модель погрешности измерений можно представить в виде:
(1.9)
где - Δinstr - инструментальная составляющая, Δmet - методическая составляющая, Δsub - субъективная составляющая погрешности измерений; символ " * " обозначает объединение составляющих погрешности измерений. Под объединением понимают некоторую операцию, позволяющую рассчитать погрешность, обусловленную совместным воздействием этих составляющих. Математически операция объединения инструментальной, методической и субъективной составляющих зависит от их структуры - соотношения в них систематических и случайных погрешностей; она базируется на математическом аппарате теории вероятностей.
По характеру поведения погрешность подразделяется на:
1. Систематическую;
2. Случайную;
3. Грубую.
Систематической погрешностью называется составляющая погрешности измерений, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Отличительная особенность таких погрешностей состоит в том, что они могут быть обнаружены и исключены из результатов измерений путем введения поправок. Однако иногда систематические погрешности чрезвычайно трудно обнаружить. В этом состоит их особая опасность. Примером систематической погрешности может служить погрешность показаний прибора за счет смещения его стрелки. Другим примером систематических погрешностей могут служить погрешности, связанные с постепенным старением средств измерений. Эти погрешности называют прогрессирующими.
Случайной погрешностью называется составляющая погрешности измерений, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности обусловлены действием различного рода факторов, изменяющихся во времени, неизвестных экспериментатору и трудно поддающихся контролю. Иногда причины возникновения случайной погрешности известны (например, действие внешних электромагнитных полей), но характер их изменения во времени также случаен. Такие погрешности трудно поддаются анализу. Для их описания используют математический аппарат теории вероятностей.
Грубая погрешность (промах) - это такая погрешность, которая существенно превышает по величине погрешность, ожидаемую при данных условиях. Примерами грубых погрешностей могут служить ошибки, допускаемые при считывании показаний приборов вследствие невнимательности экспериментатора, кратковременных сбоев в электропитании средств измерений и т.п. Грубые погрешности к рассмотрению не принимаются и исключаются из результатов наблюдений.
1.10. Полоса погрешности средств измерений
Погрешности средств измерений обусловлены их несовершенством и возрастают по мере эксплуатации из-за износа трущихся деталей, деформации упругих элементов, изменения характеристик электрических схем, и т.п.
В общем случае, средство измерений можно рассматривать как некоторый преобразователь, который преобразует входную величину (ХВХ) в выходную (ХВЫХ):
Каждому средству измерений предписывается (ставится в соответствие) так называемая номинальная функция преобразования.
Номинальная функция преобразования - это характеристика идеального средства измерений, работающего без погрешностей. Она отражает связь между входной и выходной величинами средства измерений. Номинальная функция преобразования указывается в паспорте средства измерений. У всех однотипных средств измерений номинальная функция преобразования одна и та же.
В то же время, каждое средство измерений имеет свою, реальную функцию преобразования, отличную от номинальной. У всех средств измерений, в том числе и однотипных, реальные функции преобразования различны. Эти отличия являются следствием индивидуальных погрешностей конкретных средств измерений.
Пример номинальной и реальной функций преобразования средства измерений изображен на следующем рис1.4:
Если на одном графике изобразить реальные функции преобразования множества однотипных средств измерений, то получим некоторую полосу, которая получила название полосы погрешности: 
За номинальную функцию преобразования принимают некоторую среднюю линию (выделена пунктиром).
Полоса погрешности показывает, что при одном и том же значении измеряемой величины (ХВХ1) значение результата измерений у средств измерений одного и того же типа с определенной вероятностью будет находиться в диапазоне
(XВЫХ1-Δ; XВЫХ1+Δ), (1.10)
где Δ - погрешность измерения, ХВЫХ1 – значение выходной величины средства измерения, соответствующее ХВХ1.
Необходимо отметить, что Δ - это диапазон вероятных значений погрешности средств измерений данного типа. У каждого конкретного средства измерений погрешность индивидуальна; в частном случае она может быть равной нулю.
Условно можно определить и границы полосы погрешности. В зависимости от вида границ полосы погрешности, различают аддитивную, мультипликативную и аддитивно-мультипликативную погрешности.
Аддитивная погрешность - это такая погрешность, диапазон вероятных значений которой не зависит от значения измеряемой величины (ХВХ):
Δ = ± a, (1.11)
где a=const.
Мультипликативная погрешность - это такая погрешность, диапазон вероятных значений которой возрастает по мере увеличения измеряемой величины, начинаясь с нуля:
Δ = ± bXВХ, (1.12)
где b=tg(α).
Аддитивно-мультипликативная погрешность – представляет собой комбинацию двух предыдущих погрешностей:
Δ = ±(a+bXВХ), (1.13)
a, b = const.
1.11. Классификация погрешностей средств измерений
В составе погрешности средства измерения выделяют:
1. Основную составляющую;
2. Дополнительную составляющую;
3. Динамическую составляющую;
4. Составляющую, обусловленную взаимодействием средства измерений и измеряемой величины.
Основная составляющая погрешности – это составляющая, определенная в нормальных условиях эксплуатации.
Любое средство измерений находится под воздействием различного рода факторов, изменяющихся во времени. Одним из таких факторов является измеряемая физическая величина. В качестве других факторов можно рассматривать величины, характеризующие окружающую среду:
1. температуру, давление, влажность окружающего воздуха;
2. напряжение и частоту питающей электрической сети;
3. параметры внешних электромагнитных полей;
4. параметры внешних механических воздействий (вибрация, шум) и др.
Эти факторы получили название влияющих величин.
Влияющая величина - это величина, не подлежащая измерению, но оказывающая воздействие на результат измерений.
От средства измерений требуется, чтобы из всего многообразия действующих на него факторов оно выделяло единственный - измеряемую величину. Однако, действие других факторов (влияющих величин) полностью исключить невозможно.
Изготовление, настройка, поверка и градуировка средств измерений осуществляется в так называемых лабораторных условиях, когда изменение влияющих величин происходит в очень узких пределах:
1. температура 20±5 оС;
2. давление 750±30 мм.рт.ст.;
3. влажность 60±15%;
4. напряжение 220±5 В.
Эти условия получили название нормальных условий эксплуатации.
В составе основной погрешности выделяют:
1) систематическую составляющую;
2) случайную составляющую;
3) составляющую, обусловленную гистерезисом (вариацию).
Систематическая составляющая основной погрешности остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины.
Случайная составляющая основной погрешности изменяется случайным образом при повторных измерениях одной и той же величины.
Вариация - это составляющая основной погрешности, вызванная тем, что реальная характеристика преобразования средства измерений ведет себя по-разному при увеличении (линия 1) и при уменьшении (линия 2) измеряемой величины:
Реальные (рабочие) условия эксплуатации средства измерений могут существенно отличаться от нормальных. Это приводит к дополнительному отклонению реальной функции преобразования средства измерений от номинальной, т.е. является причиной дополнительной погрешности.
Дополнительная составляющая погрешности – это составляющая, обусловленная отклонением какой-либо влияющей величины от своего нормального значения.
Динамическая составляющая погрешности средства измерений - это составляющая, обусловленная тем, что инерционные свойства средства измерений не соответствуют скорости изменения измеряемой величины.
На рис. 1.11 представлены графики изменения входного и выходного сигнала средства измерений во времени.
Любое средство измерений обладает некоторой инерцией, т.е. запаздыванием реакции на изменение входного сигнала.
Составляющая, обусловленную взаимодействием средства измерений и измеряемой величины. В практике измерений распространенным является случай, когда средство измерений может оказывать влияние на измеряемую величину. Значение измеряемой величины может измениться из-за установки средства измерений. Например, при измерении напряжения вольтметром с конечным сопротивлением, измеряемое напряжение может измениться (вследствие шунтирования участка цепи прибором). Классификация погрешностей средств измерений приведена на рис. 1.12.
1.12. Аналитическое оценивание составляющих погрешности средства измерений
Аналитическое определение погрешности производится по паспортным данным средства измерений, без проведения каких-либо экспериментов.
Погрешность средства измерений включает в себя:
1) основную составляющую;
2) дополнительную составляющую;
3) динамическую составляющую;
4) составляющую, обусловленную взаимодействием с объектом измерений.
Процедура аналитического оценивания погрешности заключается в определении характеристик (математических ожиданий и среднеквадратических отклонений) всех перечисленных составляющих инструментальной погрешности, и в расчете доверительного интервала инструментальной погрешности - т.е. интервала, в котором указанная погрешность находится с заданной вероятностью, равной 95%.
Определение характеристик основной составляющей инструментальной погрешности.
Математическое ожидание основной составляющей инструментальной погрешности:
. (1.14)
Среднеквадратическое отклонение основной составляющей инструментальной погрешности:
. (1.15)
Определение характеристик дополнительной составляющей инструментальной погрешности.
Математическое ожидание дополнительной составляющей инструментальной погрешности:
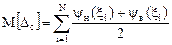, (1.16)
где 
и 
- соответственно нижняя и верхняя границы дополнительной погрешности, вызванной отклонением 
влияющей величины от своего нормального значения; N - количество влияющих величин, отклонившихся от своего нормального значения.
Среднеквадратическое отклонение дополнительной составляющей инструментальной погрешности:
. (1.17)
Определение характеристик динамической составляющей инструментальной погрешности.
Математическое ожидание динамической составляющей инструментальной погрешности:
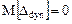(1.18)
Среднеквадратическое отклонение динамической составляющей инструментальной погрешности:
, (1.19)
где τ - запаздывание средства измерений, Т - период колебания параметра, XN - нормированное значение измеряемой величины (диапазон измерения).
Определение характеристик составляющей инструментальной погрешности, обусловленной взаимодействием с объектом измерения.
Способы оценки характеристик составляющей инструментальной погрешности, обусловленной взаимодействием с объектом измерения, зависят от характера этого взаимодействия и от характеристик средства измерений, отражающих его способности к этому взаимодействию. Например, при измерении температуры пара эта погрешность может быть обусловлена торможением потока пара, отводом тепла по арматуре термоприемника, лучистым теплообменом и другими причинами. Дать общие рекомендации по оценке значения величины Δint не представляется возможным.
Определение характеристик инструментальной погрешности.
Математическое ожидание инструментальной погрешности:
. (1.20)
Среднеквадратическое отклонение инструментальной погрешности:
. (1.21)
Доверительный интервал инструментальной погрешности:
. (1.22)
1.13. Метрологические показатели и характеристики средств измерений
При выборе средств измерений необходимо учитывать их метрологические показатели. К ним относятся:
1. Длина деления шкалы – это расстояние между серединами двух соседних отметок шкалы;
2. Цена деления шкалы – это разность значений величин, соответствующих двум соседним отметкам шкалы;
3. Функция преобразования – зависимость между входной и выходной величинами средства измерения;
4. Диапазон показаний – область значений шкалы, ограниченная конечным и начальным ее значениями;
5. Диапазон измерений – область значений измеряемой величины, в пределах которой нормированы допускаемые пределы погрешности средства измерений;
6. Чувствительность средства измерений – это отношение изменения сигнала на выходе к изменению сигнала на входе средства измерения;
7. Вариация – это наибольшая разность между показаниями прибора при измерении одной и той же величины;
8. Стабильность средства измерений – это свойство, выражающее стабильность его метрологических характеристик во времени.
Метрологические характеристики - это характеристики, предназначенные для оценки качества средств измерений (СИ) и характеристик инструментальной составляющей погрешности СИ.
Индивидуальные характеристики погрешности однотипных средств измерений (СИ) отличаются друг от друга. Поэтому, для однотипных СИ устанавливают предельные (максимально допустимые) значения характеристик погрешности, одинаковые для всех СИ данного типа. Полученные таким образом характеристики получили название нормируемых метрологических характеристик. Они указываются в паспортах СИ.
ГОСТ 8.401-80 (Классы точности средств измерений. Общие положения) предусматривает нормирование следующих величин:
1. пределов допускаемой основной погрешности (ΔOP) и соответствующих нормальных условий эксплуатации;
2. пределов допускаемой дополнительной погрешности (ΔCP) и соответствующих диапазонов изменения влияющих величин;
3. пределов допускаемой вариации (HP).
Нормирование основной составляющей инструментальной погрешности.
Предельное значение основной составляющей инструментальной погрешности указывается в виде класса точности на шкале средства измерений.
1. Если погрешность средства измерений мультипликативная:
ΔO = ± bXД, (1.23)
то класс точности S равен предельному значению основной относительной погрешности:
. (1.24)
В этом случае класс точности указывается на шкале прибора в круге.
Пример:
|
2. Если погрешность средства измерений аддитивная:
ΔO = ± a, (1.25)
то класс точности S равен предельному значению основной приведенной погрешности:
. (1.26)
В этом случае класс точности указывается на шкале прибора без каких - либо дополнительных обозначений.
Пример:
1,5.
3. Если погрешность средства измерений аддитивно - мультипликативная:
Δ = ±(a+bXД), (1.27)
то класс точности S вычисляется по следующему выражению:
, (1.28)
где
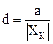, (1.29)
c = b + d, (1.30)
XК - верхний предел измерения прибора.
В этом случае класс точности указывается на шкале прибора в виде отношения c/d.
