ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y=f(x) имеет определенное значение.
Рассмотрим два значения аргумента: исходное x 0 и новое x.  Разность x– x 0называется приращением аргумента x в точке x 0 и обозначается Δx. Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx).
Разность x– x 0называется приращением аргумента x в точке x 0 и обозначается Δx. Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx).
Разность y – y 0 = f(x) – f(x 0 ) называется приращением функции y = f(x) в точке x 0 и обозначается символом Δy. Таким образом,
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ). | (1) |
Обычно исходное значение аргумента x 0 считается фиксированным, а новое значение x – переменным. Тогда y 0 = f(x 0 ) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δx также будут переменными и формула (1) показывает, что Dy является функцией переменной Δx.
Составим отношение приращения функции к приращению аргумента

Найдем предел этого отношения при Δx →0. Если этот предел существует, то его называют производной данной функции f(x) в точке x 0 и обозначают f '(x 0). Итак,
 .
.
Производной данной функции y = f(x) в точке x 0 называется предел отношения приращения функции Δ y к приращению аргумента Δ x, когда последнее произвольным образом стремится к нулю.
Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x)
Производная обозначается символами f ' (x),y ',  . Конкретное значение производной при x = a обозначается f '(a) или y ' |x=a.
. Конкретное значение производной при x = a обозначается f '(a) или y ' |x=a.
Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
Для непосредственного нахождения производной по определению можно применить следующее практическое правило:
- Придать x приращение Δ x и найти наращенное значение функции f(x + Δx).
- Найти приращение функции Δy = f(x + Δx) – f(x).
- Составить отношение
 и найти предел этого отношения при Δ x ∞0.
и найти предел этого отношения при Δ x ∞0.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
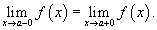 Такая точка называется точкой устранимого разрыва.
Такая точка называется точкой устранимого разрыва.
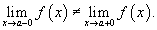 Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов
Такая точка называется точкой конечного разрыва. Модуль разности значений односторонних пределов  называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. называется скачком функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
|
| Пример 1 |
Исследовать функцию 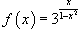 на непрерывность.
Решение.
Данная функция не определена в точках x = − 1 и x = 1. Следовательно, функция имеет разрывы в точках x = ± 1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках. на непрерывность.
Решение.
Данная функция не определена в точках x = − 1 и x = 1. Следовательно, функция имеет разрывы в точках x = ± 1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках.
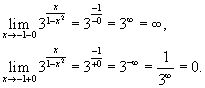 Поскольку левосторонний предел при x = − 1 равен бесконечности, то данная точка является точкой разрыва второго рода.
Поскольку левосторонний предел при x = − 1 равен бесконечности, то данная точка является точкой разрыва второго рода.

|
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга).
Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку.
| Функция y = arcsin x Дана функция y = sin x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcsin x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — \left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]. Так как для функции y = sin x на интервале \left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ] каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция y = arcsin x, график которой симметричен графику функции y = sin x на отрезке \left [ -\frac{\pi}{2}; \frac{\pi}{2} \right ]относительно прямой y = x. | 
|
| Функция y = arccos x Дана функция y = cos x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0;\pi]. На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;\pi] существует обратная функция y =arccosx, график которой симметричен графику y = cos x на отрезке [0;\pi] относительно прямой y = x. | 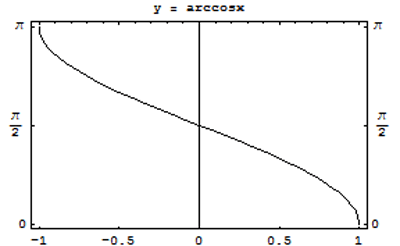
|
| Функция y = arctg x Дана функция y = tg x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arctgx функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — \left(-\frac{\pi}{2}; \frac{\pi}{2} \right). На этом отрезке y = tg x строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале \left(-\frac{\pi}{2}; \frac{\pi}{2} \right) существует обратная функция y = arctg x, график которой симметричен графику y = tgx на отрезке \left(-\frac{\pi}{2}; \frac{\pi}{2} \right) относительно прямой y = x. | 
|
| Функция y = arcctg x Дана функция y = ctg x. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arcctg x функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (0;\pi). На этом отрезке y = ctg x строго возрастает и принимает все свои значения только один раз, следовательно, на интервале (0;\pi) существует обратная функция y = arcctg x, график которой симметричен графику y = ctg x на отрезке (0;\pi) относительно прямой y = x. | 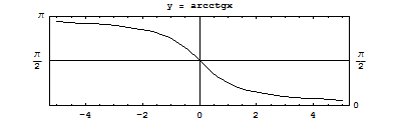
|





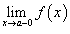 и правосторонний предел
и правосторонний предел  ;
;
