Свойства
§ У любого ограниченного числового множества, имеющего бесконечное число элементов, существуют и верхняя, и нижняя предельные точки (в множестве вещественных чисел). Если добавить в множество вещественных чисел  и
и  , то в получившемся множестве предельные точки имеют вообще все числовые множества с бесконечным числом элементов.
, то в получившемся множестве предельные точки имеют вообще все числовые множества с бесконечным числом элементов.
§ Из элементов любого ограниченного числового множества, имеющего бесконечное число элементов, можно выделить сходящуюся последовательность, элементы которой попарно различны.
Предельная точка последовательности
Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности.
 — предельная точка последовательности
— предельная точка последовательности 

Наибольшая предельная точка последовательности называется её верхним пределом, а наименьшая предельная точка — нижним пределом.
Иногда в множество возможных предельных точек включают « » и «
» и « ». Так если из последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой отрицательны, то говорят, что «
». Так если из последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой отрицательны, то говорят, что « » является предельной точкой этой последовательности. Если же из последовательности можно выделить бесконечно большую подпоследовательность с исключительно положительными элементами, то говорят, что «
» является предельной точкой этой последовательности. Если же из последовательности можно выделить бесконечно большую подпоследовательность с исключительно положительными элементами, то говорят, что « » является её предельной точкой.[1] При этом, разумеется, у последовательности могут быть и другие предельные точки.
» является её предельной точкой.[1] При этом, разумеется, у последовательности могут быть и другие предельные точки.
Свойства
§ Точка является предельной точкой последовательности тогда и только тогда, когда из этой последовательности можно выделить подпоследовательность, сходящуюся к этой точке.
 — предельная точка последовательности
— предельная точка последовательности 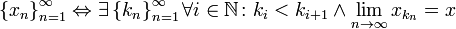
Иногда это свойство принимают за определение, а приведённое выше определение — за свойство.
§ Всякая сходящаяся числовая последовательность имеет только одну предельную точку.
 — предельные точки последовательности
— предельные точки последовательности 
§ Предельная точка любой сходящейся числовой последовательности совпадает с её пределом.
 — предельная точка последовательности
— предельная точка последовательности 
§ Для любого конечного или счётного множества точек можно построить последовательность, для которой эти точки будут являться предельными и никакие, кроме них.
§ У произвольной числовой последовальности имеется хотя бы одна предельная точка (либо вещественная, либо бесконечность).
Примеры
§ У последовательности из единиц  существует единственная предельная точка 1.
существует единственная предельная точка 1.
§ У последовательности  существует единственная предельная точка 0.
существует единственная предельная точка 0.
§ У последовательности натуральных чисел  нет предельных точек (или, в других терминах, имеется предельная точка
нет предельных точек (или, в других терминах, имеется предельная точка  ).
).
§ У последовательности  существуют две предельные точки: -1 и +1.
существуют две предельные точки: -1 и +1.
§ У последовательности из всех рациональных чисел  , занумерованных произвольным образом, существует бесконечно много предельных точек.
, занумерованных произвольным образом, существует бесконечно много предельных точек.
Предел последовательности
Если каждому натуральному числу n поставлено в соответствие некоторое вещественное число  то говорят, что задана числовая последовательность
то говорят, что задана числовая последовательность  Кратко она обозначается символом
Кратко она обозначается символом 
 называют n-м членом последовательности. Совокупность этих чисел называют множеством значений последовательности.
называют n-м членом последовательности. Совокупность этих чисел называют множеством значений последовательности.
Существует несколько способов задания числовых последовательностей.
1. Последовательность может быть задана при помощи формулы, позволяющей вычислить каждый ее член по номеру (например, 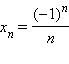 ).
).
2. Часто последовательность задается при помощи рекуррентной формулы, позволяющей определить каждый член последовательности по одному или нескольким предыдущим; при этом необходимо задание одного или нескольких первых членов последовательности. К таковым относятся арифметическая игеометрическая прогрессии или, например, последовательность Фибоначчи, задаваемая формулой
| xn + 2 = xn + 1 + xn при n > 0 |
3. и условиями x 1 = 1, x 2 = 1.
4. Иногда последовательность задается описанием ее членов, например, последовательность, у которой xn равен n -му знаку после запятой в десятичной записи числа π = 3,14159265358979323..., задается следующим образом: x 1 = 1, x 2 = 4, x 3 = 1, x 4 = 5, x 5 = 9, x 6 = 2, x 7 = 6, x 8 = 5, x 9 = 3, x 10 = 5 и т. д.
Число a называется пределом последовательности { xn }, если для каждого ε > 0 существует такой номер N ε, что для всех n ≥ N ε выполняется неравенство
| | xn – a | < ε, |
т. е.  При этом пишут, что
При этом пишут, что  или
или  при n → ∞. Кратко это определение можно записать так:
при n → ∞. Кратко это определение можно записать так:

|
Интервал (a – ε; a + ε) называют ε-окрестностью точки a.

|
| Рисунок 1.1.1.1. ε-окрестность точки a. |
Проще говоря, число a называется пределом последовательности { xn }, если в любой ε-окрестности точки a лежат все члены последовательности { xn }, за исключением, может быть, конечного их числа. Отсюда легко заметить, что изменение конечного числа членов последовательности не влияет ни на факт существования предела, ни на величину последнего.
Так, если  то
то  Действительно, выбрав для произвольного ε > 0
Действительно, выбрав для произвольного ε > 0  получаем
получаем  , так как
, так как 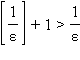 . Здесь существенно, что N ε зависит от ε.
. Здесь существенно, что N ε зависит от ε.
Для стабилизирующейся последовательности (т. е. последовательности { xn } такой, что xn = a при n ≥ n 0) в качестве N ε для любого ε можно взять n 0.
Последовательность, у которой существует предел, называется сходящейся. Если никакое число не является пределом последовательности, то она называется расходящейся.
Можно показать, что числовая последовательность имеет только один предел.
Последовательность  называется возрастающей, если для любого
называется возрастающей, если для любого  выполняется неравенство
выполняется неравенство
| xn + 1 > xn. |
Последовательность  называется убывающей, если для любого
называется убывающей, если для любого  выполняется неравенство
выполняется неравенство
| xn + 1 < xn. |
Если в этих определениях неравенство будет нестрогим, то последовательности будут называться соответственно неубывающей и невозрастающей.
Возрастающие и убывающие последовательности называют строго монотонными. Неубывающие и невозрастающие последовательности называют монотонными.
При a > 0, a \ne 1, определена функция y=ax , отличная от постоянной. Эта функция называется показательной функцией с основанием a.

Основные свойства показательной функцииy = a x при a > 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+ ∞).
- Функция строго монотонно возрастает на всей числовой прямой, то есть, если x 1 < x 2, то ax 1 < ax 2.
- При x = 0 значение функции равно 1.
- Если x > 0, то ax > 1 и если x < 0, то 0 < a < 1.
Графики показательных функций с основанием 0 < a < 1 и a > 1 изображены на рисунке.

| 
|
Основные свойства показательной функцииy = a x при 0 < a < 1:
- Область определения функции - вся числовая прямая.
- Область значений функции - промежуток (0;+∞).
- Функция строго монотонно возрастает на всей числовой прямой, то есть, если x 1 < x 2, то ax 1 > ax 2.
- При x = 0 значение функции равно 1.
- Если x > 0, то 0 < a < 1 и если x < 0, то ax > 1.
Функция и её свойства
Функция- зависимость переменной у от переменной x, если
каждому значению х соответствует единственное значение у.
Переменная х- независимая переменная или аргумент.
Переменная у- зависимая переменная
Значение функции- значение у, соответствующее заданному значению х.
Область определения функции- все значения, которые принимает независимая
переменная.
Область значений функции (множество значений)- все значения, которые
принимает функция.
Функция является четной- если для любого х из области определения
функции выполняется равенство f(x)=f(-x)
Функция является нечетной- если для любого х из области
определения функции выполняется равенство f(-x)=-f(x)
Возрастающая функция- если для любых х1 и х2
, таких, что х1< х2, выполняется
неравенство f(х1)<f(х2)
Убывающая функция- если для любых х1 и х2
, таких, что х1< х2, выполняется
неравенство f(х1)>f(х2)
Способы задания функции
¨ Чтобы задать функцию, нужно указать способ, с помощью которого для
каждого значения аргумента можно найти соответствующее значение функции.
Наиболее употребительным является способ задания функции с помощью формулы
у=f(x), где f(x)-
íåêîòîðîå
âыðàæåíèå с переменной х
. В таком случае говорят, что функция задана формулой или что функция задана
Аналитически.
¨ На практике часто используется табличный способ задания
функции. При этом способе приводится таблица, указывающая значения функции для
имеющихся в таблице значений аргумента. Примерами табличного задания функции
являются таблица квадратов, таблица кубов.
Виды функций и их свойства
1) Постоянная функция- функция, заданная формулой у=b, где
b- некоторое число. Графиком постоянной функции у=b является прямая,
параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат
2) Прямая пропорциональность- функция, заданная формулой у=kx,
где к¹0. Число k называется коэффициентом пропорциональности
.
Cвойства функции y=kx:
1. Область определения функции- множество всех действительных чисел
2. y=kx - нечетная функция
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
3) Линейная функция- функция, которая задана формулой y=kx+b, где
k и b- действительные числа. Если в частности, k=0, то
получаем постоянную функцию y=b; если b=0, то получаем прямую
пропорциональность y=kx.
Свойства функции y=kx+b:
1. Область определения- множество всех действительных чисел
2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
Графиком функции является прямая.
4) Обратная пропорциональность- функция, заданная формулой y=k/х,
где k¹0 Число k называют коэффициентом обратной
Пропорциональности.
Свойства функции y=k/x:
1. Область определения- множество всех действительных чисел кроме нуля
2. y=k/x- нечетная функция
3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке
(-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на
промежутке (0;+¥).
Графиком функции является гипербола.
5) Функция y=x2
Свойства функции y=x2:
1. Область определения- вся числовая прямая
2. y=x2 - четная функция
3. На промежутке [0;+¥) функция возрастает
4. На промежутке (-¥;0] функция убывает
Графиком функции является парабола.
6) Функция y=x3
Свойства функции y=x3:
1. Область определения- вся числовая прямая
2. y=x3 -нечетная функция
3. Функция возрастает на всей числовой прямой
Графиком функции является кубическая парабола
7) Степенная функция с натуральным показателем- функция, заданная формулой
y=xn, где n - натуральное число. При n=1 получаем функцию
y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x2;
y=x3. Их свойства рассмотрены выше.
Пусть n- произвольное четное число, большее двух: 4,6,8... В этом случае функция
y=xn обладает теми же свойствами, что и функция y=x2.
График функции напоминает параболу y=x2, только ветви графика при
|х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем «теснее
прижимаются» к оси Х, чем больше n.
Пусть n- произвольное нечетное число, большее трех: 5,7,9... В этом случае
функция y=xn обладает теми же свойствами, что и функция y=x
3. График функции напоминает кубическую параболу.
8) Степенная функция с целым отрицательным показателем- функция, заданная
формулой y=x-n, где n - натуральное число. При n=1
получаем y=1/х, свойства этой функции рассмотрены в п.4.
Пусть n- нечетное число, большее единицы: 3,5,7... В этом случае функция y=x
-n обладает в основном теми же свойствами, что и функция y=1/х.
Пусть n- четное число, например n=2.
Свойства функции y=x-2:
1. Функция определена при всех x¹0
2. y=x-2 - четная функция
3. Функция убывает на (0;+¥) и возрастает на (-¥;0).
Теми же свойствами обладают любые функции при четном n, большем двух.
9) Функция y=Öх
Свойства функции y=Öх:
1. Область определения - луч [0;+¥).
2. Функция y=Öх - общего вида
3. Функция возрастает на луче [0;+¥).
10) Функция y=3Öх
Свойства функции y=3Öх:
1. Область определения- вся числовая прямая
2. Функция y=3Öх нечетна.
3. Функция возрастает на всей числовой прямой.
11) Функция y=nÖх
При четном n функция обладает теми же свойствами, что и функция y=Öх
. При нечетном n функция y=nÖх обладает теми же
свойствами, что и функция y=3Öх.
12) Степенная функция с положительным дробным показателем- функция,
заданная формулой y=xr, где r - положительная
несократимая дробь.
Свойства функции y=xr:
1. Область определения- луч [0;+¥).
2. Функция общего вида
3. Функция возрастает на [0;+¥).
На рисунке изображен график функции y=x5/2. Он заключен
между графиками функций y=x2 и y=x3, заданных на
промежутке [0;+¥).Подобный вид имеет любой график функции вида y=x
r, где r>1.
На рисунке изображен график функции y=x2/3. Подобный вид
имеет график любой степенной функции y=xr, где 0<r<1
13) Степенная функция с отрицательным дробным показателем- функция,
заданная формулой y=x-r, где r - положительная
несократимая дробь.
Свойства функции y=x-r:
1. Обл. определения -промежуток (0;+¥)
2. Функция общего вида
3. Функция убывает на (0;+¥)
14) Обратная функция
Если функция y=f(x) такова, что для любого ее значения yo
уравнение f(x)=yo имеет относительно х единственный
корень, то говорят, что функция f обратима.
Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и
областью ее значений является промежуток Y, то у нее существует обратная
функция, причем обратная функция определена и возрастает(убывает) на Y.
Таким образом, чтобы построить график функции, обратной к функции y=f(x),
надо график функции y=f(x) подвергнуть преобразованию симметрии относительно
прямой y=x.
15) Сложная функция- функция, аргументом которой является другая любая функция.
Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2.
Получается: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции - это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
7) Периодичность функции.
Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Функция вида y = loga х (где а > 0, а ≠ 1) называется логарифмической.
1) Область определения логарифмической функции — множество всех положительных чисел.
Это следует из определения логарифма, так как выражение logax имеет смысл только при x > 0.
2) Множество значений логарифмической функции — множество R всех действительных чисел.
Это следует из того, что для любого действительного числа b есть такое положительное число x, что logax = b, т.е. уравнение logax = b имеет корень. Такой корень существует и равен x = ab, так как logaab = b.
3) Логарифмическая функция y = logax является возрастающей на промежутке x > 0, если a > 0, и убывающей, если 0 < a < 1.
4) Если a > 0, то функция y = logax принимает положительные значения при x > 1, отрицательные — при 0 < x < 1. Если 0 < a < 1, то функция y = logax принимает положительные значения при 0 < x < 1, отрицательные — при x > 1.
Это следует из того, что функция y = logax принимает значение, равное нулю, при x = 1 и является возрастающей на промежутке x > 0, если a > 1, и убывающей, если 0 > a > 1.
Ниже представлены графики логарифмических функций при a > 0 (1); 0 > a >1 (2).

Стоит отметить, что график любой логарифмической функции y = logax проходит через точку (1; 0)
Алгоритм решения.
- Подставить в выражение предельное значение аргумента.
- Определить есть или нет неопределенность. Если нет, дать ответ.
- Если неопределенность есть, то по ее виду выбрать одно из правил устранения этой неопределенности.
- Преобразовать выражение согласно выбранному правилу, и к новой форме предела применить данный алгоритм, начиная с п.1.
Правило 1.
 В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что
В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что 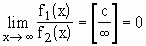 , а
, а  , где c - любое число.
, где c - любое число.
Правило 2.
 Числитель и знаменатель разделить одновременно на
Числитель и знаменатель разделить одновременно на  , если это возможно. Необходимо иметь в виду, что
, если это возможно. Необходимо иметь в виду, что  , а
, а  , где c - число, отличное от нуля.
, где c - число, отличное от нуля.
Правило 3.
При вычислении пределов от иррациональных выражений, не попадающих в предыдущие правила, следует избавиться от корней, входящих в неопределенность. Возможны следующие способы:
3.1. замена переменной  , позволяющая извлечь корни, входящие в неопределенность;
, позволяющая извлечь корни, входящие в неопределенность;
3.2. дополнение до формулы, позволяющей возвести корень в соответствующую ему степень; здесь используются формулы:  ;
;  .
.
Например, 
 , т.е. умножили и разделили на сопряженное выражение.
, т.е. умножили и разделили на сопряженное выражение.
Правило 4.
При наличии неопределенности в пределе от выражения, содержащего тригонометрические функции, следует выделить в этом выражении первый замечательный предел:
 . (1)
. (1)
Можно использовать следствия этого предела:
 ; (2)
; (2)
 ; (3)
; (3)
 ; (4)
; (4)
 . (5)
. (5)
Свойства пределов функции
1) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
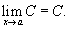
2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы:
Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:







