Пусть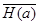 
- производительность источника, тогда, если производительность источника меньше пропускной способности канала (
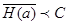), то можно передовать сообщения со сколь угодно высокой достоверностью.
Шеннон впервые указал на то, что можно сделать. Ему принадлежит идея помехоустойчивого кода. Ранее, до Шеннона, повышение помехоустойчивости достигалось многократной передачи одной и той же информации и вынесением решения по большинству голосов. Это было крайне не рационально для канала, так как для передачи требовалось большее время. Теорема Шеннона, хотя и не конструктивна, утверждает что достоверность можно повысить другим методом – путем построения помехоустойчивого кода. В дальнейшем это положение было подробно разработано с применением математического аппарата комбинаторики и в теории связи появилось научное направление "помехоустойчивое кодирование". В данном разделе мы не будем его подробно рассматривать, а ограничимся изучение помехоустойчивого кода с проверкой на четность. Формирование этого кода идет по схеме показанной на рис.2.
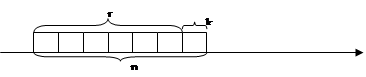Кодер канала формирует помехоустойчивый код по первичному коду сообщения. Рассмотрим как это делается. Допустим первичный код представлен r разрядами (в данном на рис.3 примере 6 разрядов).
Рис.3
В комбинацию кода вводится еще один разряд k, который называется контрольным. Его значение определяется по очень простому правилу: количество единиц во всем кодовом слове должно быть четным. Например, r разрядов 011101, контрольный разряд k равен 0; r – 001110, k – 1. Это правило формирования кода известно в приемнике и его задача проверить выполнение условия. Если количество единиц четное, ошибок нет и информация поступает получателю. Если же нет, приемник вырабатывает сигнал ошибки, по которому запрашивается повторная передача. Такое правило позволяет обнаружить однократные ошибки. Существуют более сложные помехоустойчивые коды не только обнаруживающие, но и исправляющие ошибки.
2.1 Ортогональные ряды. Рассмотрим такие ряды подробнее. Это определение накладывает свой отпечаток прежде всего на свойство базисных функций. Ряд ортогонален, если
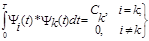. (3)
 |
Введем новые базисные функции нормированные следующим образом:
Свойство нормированных ортогональных базисных функций следующее:
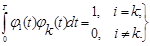(4)
Заданный сигнал теперь запишется так:
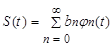, (5)
а сам ряд получил название ортонормированного ряда.
Далее разберем как находить коэффициенты bk. Для этого в (5) умножим левую и правую часть на jk b проинтегрируем произведения за период:
. (6)
Воспользовавшись свойством ортогональности в правой части, получим
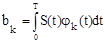. (7)
Интеграл в (7) легко может быть вычислен любым способом.
Представление сигнала в виде ортогонального ряда позволяет получить полные сведения о сигнале в более сжатой форме, т.е. ту же информацию, но при меньшем количестве параметров. В теории сигналов в основном применяются ортогональные ряды Фурье, Уолша и Котельникова.
Средняя мощность периодического сигнала
Важность этой характеристики заключается в том, что она отражает не только величину сигнала, но и его длительность. Это необходимо учитывать при приеме сигнала, при его различении. Известно, что средняя за период мощность равна
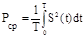. (18)
Выразим S(t) через ряд Фурье:
 |
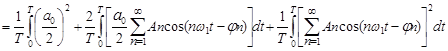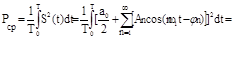
(19)
Первый интеграл в (19) выражает мощность постоянной составляющей сигнала:
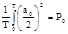. (20)
Второй интеграл, берется от знакопеременной функции, имеющей целое число периодов на интервале интегрирования T. При любом n он будет равен нулю.
Прежде чем решать третий интеграл проведем анализ подынтегральной функции. Обратимся к простому примеру. Допустим вместо бесконечной суммы имеем квадрат трехчлена:
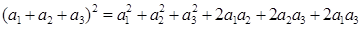(21)
В этом простом выражении есть сумма квадратов членов и сумма произведений различных членов с дополнительным коэффициентом. Таким образом подынтегральное выражение может быть записано в виде двух сумм и третий интеграл в (19) будет:
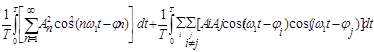. (22)
Интеграл от двойной суммы будет равен нулю по свойству ортогональности, а первый представляет собой хорошо известное выражение средней мощности гармонического сигнала, в качестве которого выступает n-ая гармоника:
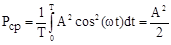. (23)
Таким образом, (22) является суммой средних мощностей гармоник,
, (24)
и искомая средняя мощность периодического сигнала будет равна
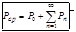(25)
Это выражение получило название «равенство Парсеваля».
Интересно заметить, что мощность не зависит от фаз гармонических составляющих сигнала и результирующая мощность складывается из мощностей отдельных гармоник.
Практическая ширина спектра
Реальные устройства систем связи и управления содержат инерционные элементы (индуктивности, емкости). Поэтому невозможно передавать по такой системе гармонические составляющие сколь-угодно больших и малых частот.
Очевидно, что передавать следует гармонические составляющие с относительно большими амплитудами, содержащими большую долю энергии.
Поэтому вводится понятие практической ширины спектра сигнала.
К нему можно подходить с 2-х точек зрения:
1. Сохранить основную энергию сигнала, т.е. учитывать ширину спектра, в которой сосредоточена подавляющая часть энергии сигнала.
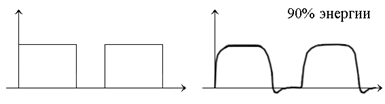
Рис. 10.3
2. Сохранить не только энергию, но и форму сигнала. Это требование резко расширяет требуемую полосу частот.
Пример
