Кодирование и модуляция.
Каждое преобразование в канале это большая и сложная тема. Мы же кратко рассмотрим два основных преобразования: кодирование и модуляция.
После аналогоцифрового преобразования любой сигнал превращается в цифровую форму. Каждому значению входного сигнала N соответствует число, обычно записанное в двоичной системе счисления. Эту операцию математически можно записать так:
 ,
,
где  - коэффициенты,
- коэффициенты,
 - число, обычно, в десятичном виде.
- число, обычно, в десятичном виде.
Набор коэффициентов 
 это и есть код одного из значений сообщения.
это и есть код одного из значений сообщения.
Таким образом, кодирование это запись десятичного числа в двоичной форме. Кодер источника преобразует код с АЦП, например, исключает избыточность источника информации (эта функция получила название сжатие). Кодер канала еще раз преобразует код, делая его помехоустойчивым. Для этого в код включается избыточность заданной величины.
Модуляция определяет вид передаваемого сигнала. Процесс этот идет следующим образом. Допустим, имеется два сигнала. Один отражает передаваемую информацию, а другой ничего не отражает и является самостоятельным. Далее допустим, что первый сигнал воздействует на второй и меняет его какой – то параметр. Следовательно, этот первоначально определенный как самостоятельный, уже будет отражать информацию. Вот в этом и заключается процесс модуляции. Модуляция состоит в том, что один из параметров сигнала изменяется во времени в соответствии с передаваемым сообщением. Сигнал у которого изменяется параметр называется сигнал – переносчик. В каналах связи в основном используются два вида сигналов – переносчиков: гармонический сигнал и импульсная последовательность. В соответствии с этим модуляции бывают гармонические и импульсные.
При гармонической модуляции у сигнала переносчика можно изменять следующие параметры: амплитуду, частоту и фазу. При этом получаем амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ) модуляцию. При АМ амплитуда меняется по закону  . При ЧМ частота
. При ЧМ частота  , при ФМ фаза определяется как
, при ФМ фаза определяется как 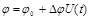 . В этих выражениях
. В этих выражениях  временная функция полезного сигнала;
временная функция полезного сигнала;  - величины изменений соответствующих параметров.
- величины изменений соответствующих параметров.
На рис.2, 3 показаны осциллограммы сигналов АМ и ЧМ соответственно при  гармонического вида.
гармонического вида.
 |  | ||
Импульсные виды модуляции бывают следующие: амплитудно-импульсная (АИМ), широтно-импульсная (ШИМ), фазо-импульсная (ФИМ) и частотно-импульсная (ЧИМ). При этом, под воздействием
 |
Рис 2 Рис 3 Рис 4
полезного сигнала изменяется соответствующий параметр импульсной последовательности. В технике связи наибольшее применение получила АИМ. На рис. 4 показан вид сигнала АИМ.
У истоков теории информации стоит Клод Шеннон, который в 1947-48 годах работал над вопросом эффективности систем связи. В результате этого была сформулирована цель данной теории – повышение пропускной способности канала связи. Эффективна та система, которая при прочих равных условиях и затратах передает большее количество информации. Обычно при анализе рассматривается объекта: источник информации и канал передачи информации.
Итак, имеются какие-то события. Информация о них в знаковой форме, в виде сигнала передается по каналу связи. Можно утверждать, что канал хороший, если он отвечает двум условиям. Во-первых, по нему передается информация с высокой скоростью и во-вторых помехи, воздействующие на передачу, снижают качество информации незначительно. Для того чтобы найти условия для такой передачи необходимо ввести какие-то информационные характеристики.
Наиболее наглядно основные положения теории информации проявляются при дискретном источнике и таком же канале. Поэтому знакомство с темой начнем при данном допущении.
1.4 Количественная мера информации.
Прежде разберемся, что имеет смысл передавать по каналу.
Если получателю известно, какая информация будет передана, то, очевидно, нет необходимости ее передачи. Есть смысл передавать только то, что является неожиданным. Чем больше эта неожиданность, тем большее количество информации должно содержаться в этом событии. Например, Вы работаете за компьютером. Сообщение о том, что сегодня работу надо закончит через 45 мин. согласно расписанию вряд ли является для Вас новым. Это абсолютно ясно было и до заявления о конце работы. Следовательно, в таком сообщении содержится нулевая информация; передавать его бессмысленно. А теперь другой пример. Сообщение следующее: через час начальник подарит Вам авиабилет до Москвы и обратно, да еще выделит сумму денег на развлечения. Такого рода информация для Вас неожиданна и, следовательно, содержит большое количество единиц меры. Вот такие сообщения имеет смысл передавать по каналу. Вывод очень простой: чем больше неожиданности в сообщении, тем большее количество информации в нем содержится.
Неожиданность характеризуется вероятностью, которая и закладывается в информационную меру.
Еще несколько примеров. Имеем два ящика, один с белыми, а другой с черными шарами. Какое количество информации содержится в сообщении, где белые шары? Вероятность того, что в любом указанном ящике белые шары равна 0,5. Назовем эту вероятность до опытной или априорной.
Теперь вытаскиваем один шар. В независимости от того, какой шар мы вынули, после такого опыта будет абсолютно точно известно в каком ящике белые шары. Следовательно, вероятность сведений будет равна 1. Эта вероятность называется после опытной или апостериорной.
Посмотрим на данную пример с позиции количества информации.итак, имеем источник информации ящики с шарами. Первоначально неопределенность о шарах характеризовалась вероятностью 0,5. Далее источник "заговорил" и выдал информацию; мы вытащили шар. Далее все стало определено с вероятностью 1. Степень уменьшения неопределенности о событии в результате опыта логично принять за количественную меру информации. В нашем примере это будет 1/0,5.
Теперь пример более сложный. Известно, что размер детали может быть 120,121,122,...,180 мм., то есть, имеет одно из 61-ого значений. Априорная вероятность того, что размер детали i мм равна 1/61.
У нас имеется весьма несовершенный измерительный инструмент позволяющий измерить деталь с точностью +5,-5 мм. В результате измерения получили размер 130 мм. Но фактически он может быть 125,126,...,135 мм.; всего 11 значений. В результате опыта остается неопределенность, которая характеризуется апостериорной вероятностью 1/11. Степень уменьшения неопределенности будет (1/11):(1/61). Как и выше это отношение и есть количество информации.
Наиболее удобна логарифмическая функция для отражения количества информации. Основание логарифма принимается равное двум. Обозначим  количество информации,
количество информации,  - априорная вероятность,
- априорная вероятность,  - апостериорная вероятность. Тогда,
- апостериорная вероятность. Тогда,
 . (1)
. (1)
В первом примере  1 бит информации; во втором
1 бит информации; во втором  2,46 бит информации. Бит – одна двоичная единица информации.
2,46 бит информации. Бит – одна двоичная единица информации.
Энтропия и ее свойства
Энтропия это среднее количество информации, приходящееся на одно событие (сообщение) источника. Находится она по правилам определения математического ожидания:
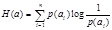 . (3)
. (3)
Или учитывая свойства логарифмической функции
 . (4)
. (4)
Размерность энтропии бит/сообщение. Остановимся на свойствах энтропии. Начнем с примера. Допустим, имеется двоичный источник информации с априорными вероятностями событий 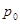 и
и  составляющих полную группу. Из этого следует связь между ними:
составляющих полную группу. Из этого следует связь между ними: 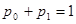 . Найдем энтропию источника:
. Найдем энтропию источника:
 . (5)
. (5)
Не трудно видеть, что если одна из вероятностей равно нулю, то вторая равна 1, а выражение энтропии при этом даст нуль.
Построим график зависимости энтропии от  (рис.1).
(рис.1).
Обратим внимание на то, что энтропия максимальна при вероятности равной 0,5 и всегда положительна.
 |
Первое свойство энтропии. Энтропия максимальна при равновероятных событиях в источнике. В нашем примере двоичного источника эта величина равна 1. Если источник не двоичный и содержит N слов, то максимальная энтропия.
Второе свойство энтропии. Если вероятность одного сообщения источника равна 1, и остальные равны нулю, как образующие полную группу событий, то энтропия равна нулю. Такой источник не генерирует информацию.
Третье свойство энтропии это теорема сложения энтропий. Разберем этот вопрос более подробно. Допустим, имеется два источника информации представленные множествами сообщений 
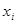 и
и 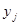 .
.
У каждого из источников имеются энтропии  и
и 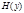 . Далее эти источники объединяются, и требуется найти энтропию объединенного ансамбля
. Далее эти источники объединяются, и требуется найти энтропию объединенного ансамбля 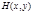 . Каждой паре сообщений
. Каждой паре сообщений 
 и
и  соответствует вероятность
соответствует вероятность  . Количество информации в такой паре будет
. Количество информации в такой паре будет
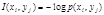 . (6)
. (6)
Действуя известным образом, найдем среднее количество информации, приходящееся на пару сообщений ансамбля. Это и будет энтропия. Правда, здесь может быть два случая. Объединяемые ансамбли могут быть статистически независимы и зависимы.
Рассмотрим первый случай независимых ансамблей, появление сообщения 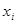 ни в коей мере не определяется
ни в коей мере не определяется 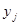 . Запишем выражение для энтропии:
. Запишем выражение для энтропии:
 , (7)
, (7)
здесь 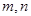 - число сообщений в ансамблях.
- число сообщений в ансамблях.
Так как при независимости двумерная вероятность  , а
, а  , из общей предыдущей формулы получим
, из общей предыдущей формулы получим
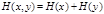 , (8)
, (8)
где 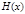 и
и  определяются по известным формулам.
определяются по известным формулам.
Далее рассмотрим более сложный случай. Предположим, что ансамбли сообщений находятся в статистической связи, то есть 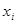 с какай-то вероятностью предполагает появление
с какай-то вероятностью предполагает появление 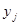 . Этот факт характеризуется условной вероятностью
. Этот факт характеризуется условной вероятностью  ; косая черта в обозначении характеризует условие. При введении условных вероятностей двумерная вероятность может быть определена через произведение одномерных:
; косая черта в обозначении характеризует условие. При введении условных вероятностей двумерная вероятность может быть определена через произведение одномерных:
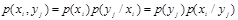 . (9)
. (9)
Учитывая это, найдем выражение для энтропии. Преобразование идет следующим образом:
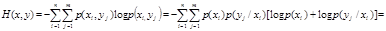
 . (10)
. (10)
Учитывая равенство 1 суммы всех вероятностей событий, первая двойная сумма в последнем выражении дает энтропию источника X, H(x).
Вторая двойная сумма получила название условной энтропии и обозначается как  . Таким образом,
. Таким образом,
 . (11)
. (11)
Аналогичным образом можно доказать, что  .
.
В последних выражениях мы встретились с условной энтропией, которая определяется связью между объединяемыми ансамблями сообщений. Если ансамбли статистически независимы  , и условная энтропия
, и условная энтропия  . В итоге мы получаем известную формулу.
. В итоге мы получаем известную формулу.
Если сообщения зависимы абсолютно, то есть находятся в функциональной связи,  принимает одно из двух значений: либо 1, когда
принимает одно из двух значений: либо 1, когда  , либо 0, когда
, либо 0, когда 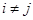 . Условная энтропия будет равна 0, так как второй ансамбль сообщений не обладает неожиданностью, и, следовательно, не несет информацию.
. Условная энтропия будет равна 0, так как второй ансамбль сообщений не обладает неожиданностью, и, следовательно, не несет информацию.
Источник информации и его характеристики
После введения энтропии и ее свойств, вернемся к единственному источнику информации. Следует знать, что любой источник информации работает в текущем времени. Его символы (знаки) занимают определенное место в последовательности. Источник информации называется стационарным, если вероятность символа не зависит от его места в последовательности. И еще одно определение. Символы источника могут иметь статистическую (вероятностную) связь друг с другом.






