При разработке часто возникают условия, при которых проницаемость в законтурной области меньше проницаемости внутри контура.
|
Пусть в круге радиуса R0 проницаемость k 1, а в кольце Rк проницаемость k2. При этом Rк>>a, радиуса батареи.
Поток к n эксплуатационным скважинам идёт от окружности радиуса R0 и дебит G1 каждой скважины определяется по (4.25) 
, где вместо jк следует поставить j0 - потенциал на границе двух сред, а вместо Rк - R0. Во второй области поток плоскорадиален от контура Rк до укрупненной скважины радиуса R0 и дебит скважины 
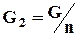, где G определяется по формуле (4.26) 
. Имея в виду, что в пределах каждой зоны k =const, распишем потенциал в виде j=kФ+С, где 
. Подставляя данное выражение для j в соотношение для дебитов и исключая Ф0 получим
. (4.57)
Для однородной несжимаемой жидкости Ф=р/h, а вместо массового дебита G/ надо подставить объёмный дебит Q. Пользуясь (4.57) можно сравнить дебиты батареи при различных относительных размерах частей I и II пласта и при различных соотношениях между проницаемостями. Расчеты показывают, что при k1/k2=b<1 величина коэффициента суммарного взаимодействия 
(отношение суммарного дебита группы совместно действующих скважин к дебиту одиночной скважины) всегда выше, чем U батареи, действующей при тех же условиях в однородном пласте (b =1). Если же b >1, то U будет меньше его значения в однородном пласте. При одних и тех же значениях b взаимодействие скважин будет тем больше, чем большую площадь при данных условиях занимает менее проницаемая часть пласта.
Рассмотрим случай, когда кольцевая батарея занимает область II, т.е. область, примыкающую к контуру питания (а>R0). В этом случае
. (4.58)
Для анизотропных пластов, т.е. где неоднородность имеет некоторую направленность, скважины взаимодействуют приблизительно также как и в анизотропном пласте. Эффект взаимодействия будет значительно усиленным или ослабленным лишь при резком различии проницаемостей в двух определённых направлениях: в направлении линии расстановки скважин и в направлении, перпендикулярном к этой линии.
Ослабление взаимодействия наблюдается в случае более низкой проницаемости в направлении линии расстановки скважин по сравнению с проницаемостью в перпендикулярном направлении. Усиление эффекта взаимодействия происходит в обратном случае. Таким образом, для уменьшения эффекта взаимодействия при закладывании новых скважин следует выбирать направление, в котором пласт наименее проницаем.
4.4. Влияние радиуса скважины на её производительность
Одиночная скважина. Определим дебит в двух крайних случаях: по закону Дарси - 1-ое в формуле (3.48) и по закону Краснопольского развитого нелинейного течения - 2-ое слагаемое. Тоже самое сделаем и в случае радиально-сферического течения. Если примем радиус одной скважины rс, а другой - rc/= xrc и, соответственно, дебиты G и G/, а их отношение обозначим через у=G/G/, то получим следующие формулы для вычисления предельных значений у
| Закон | Тип потока | |
| фильтрации | плоскорадиальный | радиально-сферический |
| Дарси | 
| у=х |
| Краснопольского | 
| 
|
Из таблицы видно, что при сохранении закона Дарси в плоскорадиальном потоке влияние радиуса скважины на дебит невелико (необходимо увеличение радиуса в 10 раз, чтобы дебит вырос на 20%). Если же фильтрация нелинейна, то влияние rc на G усиливается. Для сферически-радиального потока дебит скважины зависит от радиуса в большей степени, особенно при нелинейном законе фильтрации. Таким образом, расширение забоя скважины способствует увеличению производительности. При торпедировании забоя, гидравлическом разрыве пласта и других способах воздействия на призабойную зону образуются и расширяются трещины, что способствует нарушению закона Дарси и, следовательно, усилению влияния радиуса скважины на приток к ней жидкости.
Взаимодействие скважин. С целью выявления влияния радиуса скважин на дебит при взаимодействии скважин сравним дебиты скважин кольцевой батареи из n эксплуатационных скважин в двух случаях: 1)скважины имеют радиус rc и 2)скважины имеют радиус хrc.
Из (4.25)
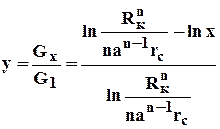. (4.59)
Кроме того, рассмотрим случай, если в центре батарей действует нагнетательная скважина с дебитом равным дебиту батареи
. (4.60)
Из данных зависимостей следует, что с увеличением числа эксплуатационных скважин кольцевой батареи влияние их радиуса на дебит уменьшается, если отсутствует нагнетание жидкости в пласт. Если в центре батареи находится нагнетательная скважина, то влияние радиуса скважины на дебит будет больше, чем при отсутствии центрального нагнетания жидкости в пласт. При этом радиус скважины влияет на производительность больше, чем при одиночной эксплуатационной скважине. Число скважин при этом несущественно. Таким образом, взаимодействие эксплуатационных скважин с нагнетательными скважинами повышает влияние радиуса скважин на дебит.
