В большинстве случаев дебит газовых скважин не следует закону Дарси, так же как в некоторых случаях и для нефтяных и водяных скважин.
Вблизи фильтрационных отверстий при приближении к стенке скважины скорость фильтрации становится настолько большой, что число Рейнольдса превосходит критическое. Квадраты скоростей становятся настолько большими, что ими пренебрегать уже нельзя.
Уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине записывается в виде, аналогично идеальному,
. (3.53)
но здесь А и В являются функциями р и Т
. (4.52)
Приток к несовершенной скважине учитывается, так же как и при фильтрации по закону Дарси, т.е. введением приведённого радиуса скважины 
в формулу дебита.
|
При нарушении закона Дарси для скважины несовершенной по степени и характеру вскрытия для расчета притока проще всего использовать следующую схему. Круговой пласт делится на три области. Первая имеет радиус R1»(2-3) rc. Здесь из-за больших скоростей вблизи перфорации происходит нарушение закона Дарси и проявляется в основном несовершенство по характеру вскрытия. Вторая область - кольцевая с R1< r< R2 и R2»h. Здесь линии тока искривляются из-за несовершенства по степени вскрытия, и фильтрация происходит тоже по двухчленному закону. В третьей области (R2< r< Rк) действует закон Дарси и течение плоскорадиально.
Для третьей области
. (4.53)
Во второй области толщина пласта переменна и изменяется по линейному закону от hвс при r=R1 до h при r=R2 (hвс - глубина вскрытия), т.е. h(r)=a+br, где a и b определяются из условий h(r)= hвс при r=R1; h(r)= h при r=R2. Чтобы получить закон движения в этой области, надо проинтегрировать уравнение (3.50) 
предварительно подставив вместо постоянной толщины h переменную h(r) и учтя реальные свойства газа
, (4.54)
где
.
С2 - вычисляется приближенно в области hвс>> R1.
В первой области фильтрация происходит по двухчленному закону и плоскорадиальное течение нарушается из-за перфорационных отверстий. Уравнение притока имеет вид (4.54), но несовершенство учитывается коэффициентами С3 и С4, а R2 заменяется на R1 и R1 - на rc.
Коэффициент С3 определяется по графикам Щурова, а для С4 предлагается приближенная формула
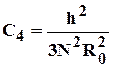, где N - суммарное число отверстий;
R0 - глубина проникновения перфорационной пули в пласт.
Складывая почленно (4.53), (4.54) и уравнение притока для первой области получим уравнение притока для несовершенной скважины
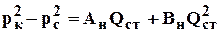, (4.55)
где
.
Интерференция скважин
В случае интерференции скважин несовершенных по степени вскрытия в условиях течения по закону Дарси вначале определяется дебит совершенных скважин радиусами rс по формулам теории интерференции для притока к стокам и источникам на плоскости, а затем фильтрационное сопротивление каждой скважины увеличивается на величину коэффициентов несовершенства Сi (i =1,...,4). Если определены коэффициенты фильтрационных сопротивлений Ан и Вн, указанным выше аналитическим оценочным методом или прямым испытанием скважины путем пробных откачек при установившемся режиме, можно использовать метод эквивалентных фильтрационных сопротивлений для исследования интерференции несовершенных скважин, в том числе при двухчленном законе фильтрации. Для этого двухчленный закон надо представить в виде
, (4.56)
где 
можно рассматривать как нелинейное сопротивление, добавляемое к внутреннему сопротивлению r, определяемому конечным расстоянием между скважинами в батарее.
Например, в схеме фильтрационных сопротивлений для условий линейного закона фильтрации, внутренние сопротивления r следует заменить суммой 
, где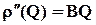 
для каждой скважины. Дальнейший расчет ведется, как и ранее, при помощи законов Ома и Кирхгофа, но система уравнений получается уже не линейной, а содержащей квадратные уравнения, что приводит к усложнению вычислений.
