Корреляционная функция прогиба пластины имеет вид:
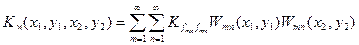 (3.1)
(3.1)
где  вычисляется по формуле (2.27).
вычисляется по формуле (2.27).
В соответствии с [1] имеем:
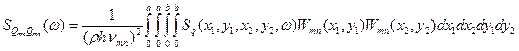 (3.2)
(3.2)
Норма собственных функций имеет вид:

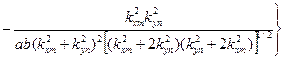 (3.3)
(3.3)
С ростом чисел m и n норма νmn приближается к ab/4.
Если подставить в (3.2) значения Wmn(x,y) соответственно с (2.38) и выполнить интегрирование, получают:
 (3.4)
(3.4)
где
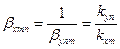 (3.5)
(3.5)
 (3.6)
(3.6)
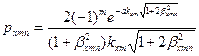 (3.7)
(3.7)
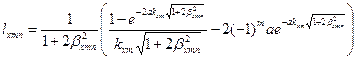 (3.8)
(3.8)
Соотношения для gynm, pynm, lynm получают путем круговой замены индексов m и n, х и у, а также параметров a и b.
Некоторые вычисления по формуле (3.1) для пластин с параметрами [3] иллюстрируются графиками. Как видно, усиление краевых условий ведет к увеличению корреляции прогибов.

Рисунок 3.1 – Корреляционная функция прогиба пластины Кw(x,y,a/45,/b/2) в случае краевых условий жесткого защемления.
Предложенный подход позволяет получить в закрытом виде асимптотическое решение задачи та исследовать влияние условия внешней нагрузки, типа демпфирования.
ВЫВОДЫ
В дипломной работе решена задача исследования всего спектра частот при сложных граничных условиях с помощью асимптотического метода. Одно из достоинств этого метода в том, что при увеличении частот возрастает также и точность вычислений.
При этом решение выражается в виде сумы внутреннего решения и поправочных решений, которые называются динамическими краевыми эффектами. Для каждой границы необходимо строить решение, удовлетворяющее дифференциальному уравнению и условиям на соответствующей границе.
Полученные решения склеивают. Благодаря этому можно получить систему трансцендентных уравнений для параметров, определяющих как внутреннее решение и краевые эффекты.
Асимптотическое решение может быть построено для всей окрестности углов и ребер.
Получены аналитеские выражения корреляционной функции прогиба пластины, стохастических колебаний пластины.
ЛИТЕРАТУРА
1. Болотин В.В. Случайные колебания упругих систем. – М.: Наука, 1979. – 46 с.
2. Прочность. Устойчивость. Колебания. Справочник. /под общей редакцией И.А. Биргера и Я.Г. Пановко/, Т.З. – М.: «Машинострой», 1968. – 310 с.
3. Диментбер М.Ф. Вынужденные колебания пластин при нагрузке, представляющей случайный процесс. //Инженерный журнал.. – 1961 г. Т.1 вып.2
4. Болотин В.В.Динамический краевой эффект. /Инженерный сборник/, – М.: Стройиздат. 1980 г.
5. Болотин В.В. Применение методов теории вероятностей и теории надежности в расчетах сооружений. – М.: Стройиздат. 1971. – 256 с.
6. Болотин В.В. Методы теории вероятностей и теории надежности в расчетах сооружений. – М.: Стройиздат. 1982. – 352 с.
7. Пановко Я.Г. Внутреннее трение при колебаниях упругих систем. – М.: Физматлит. 1960. – 193 с.
8. Сорокин Е.С. К теории внутреннего трения при колебаниях механических систем. – М.: Гостстройиздат. 1960. – 129 с.
9. Тимошенко С.П. и Войновский – Кригер С. Пластины и оболочки. – М.: Наука. 1966. – 635 с.
10. Физический энциклопедический словарь/под ред. А.М. Прохорова. – М.: Советская энциклопедия, 1983. – 724 с.
11. Пугачев В.С., Синицын И.Н. Стохастические дифференциальные сиситемы. – М.: Наука, 1985. – 69 с.
12. Бендат Дж. Пирсон А. Изменение и анализ случайных данных. – М.: Мир, 1971. – 408 с.
13. Бендат Дж. Пирсон А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 137 с.
14. Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления. – М.: Физматлит. 1960. – 883 с




