Имеется широкий круг проблем строительной механики, применение статистических методов к которым вполне оправдано и, более того, для которых статистические методы являются наиболее адекватным средством исследования. Поэтому целесообразно ввести такие понятия как случайная величина нагрузки и случайный процесс нагружения.
Под нагрузками понимаются не только внешние силы, но и внешние кинематические воздействия – заданные перемещения системы или ее отдельных точек, а также тепловые воздействия, излучения и т.п.
Будем различать два основных класса случайных нагрузок — нагрузки, задаваемые в виде случайных функций времени, и нагрузки, задаваемые в виде случайных функций времени и координат.
Описание первого класса нагрузок осуществляется методами теории случайных процессов, для описания второго класса требуется привлечение теории случайных полей [1,11,14].
Функции, значения которых при фиксированных значениях аргументов являются случайными величинами, называется случайными функциями. В прикладных задачах аргументом случайных функций часто является время; случайные функции времени называют обычно случайными процессами. Пульсации скорости и давления в турбулентном потоке, шум реактивного двигателя, толчки, испытываемые транспортным средством при движении по неровному пути, представляют собой случайные процессы.
Пусть внешнее воздействие характеризуется элементами q из пространства Q, а поведение системы u из пространства U. Математическая природа элементов обоих пространств, вообще говоря, произвольна. Это могут быть числа, векторы, тензоры, функции одной или нескольких переменных и т.п.
Вместо полного вероятностного описания путем задания меры в функциональных пространствах нередко используется частичное описание. При этом широко применяются интегралы по вероятностной мере: математические описания, дисперсии и другие моменты от случайных величии, моментные и корреляционные функции от случайных процессов. Вероятность случайного события интерпретируется как объективная мера, эквивалентная эмпирической частоте.
Для получения вероятностных характеристик системы необходимо иметь соответствующую статистическую информацию. Но в распоряжении экспериментатора очень редко находится количество экземпляров, достаточное для того, чтобы делать надежные статистические выводы, К счастью многие вероятностные свойства систем обладают эргодичностью. Эти свойства проявляются не только в ансамбле реализаций, но и во времени и в пространстве. Такие вероятностные свойства можно изучать, наблюдая за поведением одного экземпляра во времени или изучая, как эти свойства меняются при переходе от одной точки к другой.
Корреляционные методы основаны на изучении связей между некоторыми характеристиками входных и выходных процессов — между корреляционными или между соответствующими родственными им функциями. Функции, описывающие статистическую связь (кореляцию) между значениями в разные моменты времени называются корреляционными функциями.
Пусть q1(t), q2(t) … qn(t) - некоторые случайные функции времени. Будем обозначать < > осреднение по ансамблю реализаций.
Рассмотрим характеристики процесса, образуемые по следующим правилам:
Kjk=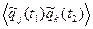 
,
Kjkm=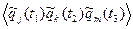 
,
,
(j, k, m= 1,2,…n) (1.6)
Характеристики Kjk, Kjkm и т.д. называются корреляционными функциями второго, третьего и т.д. порядков. для исчерпывающего описания процесса необходимо знать полную систему корреляционных функций.
Значительная часть информации о случайном процессе все же заключена в средних < q(t) > и корреляционных функциях второго порядка
В ряде задач (например, в тех задачах, где заранее известно, что обобщенные координаты подчиняются нормальному распределению) указанных характеристик достаточно для построения совместных плотностей вероятностей и последующего решения вопросов надежности.
Описание случайного процесса упрощается, если он является стационарным, т.е. если все его статистические характеристики остаются неизменными во времени.
Средние значения для стационарного случайного процесса постоянны, а корреляционные функции зависят лишь от разностей t1-t2, t1- t3 и т.д. В частности, корреляционные функции второго порядка выражаются по формулам:
Kjk(τ)=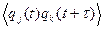 
(1.7)
Почти все представляющие интерес стационарные случайные нагрузки обладают также свойством эргодичности. Для эргодических случайных процессов осреднение по ансамблю реализаций может быть заменено осреднением по времени.
В частности,
Kjk(τ)=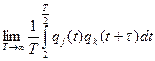 
(1.8)
Введем также представление Фурье для корреляционной функции
Kjk(τ)=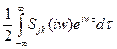 
(1.9)
Функции Sjk(τw) - будем называть совместными спектральными плотностями. Если процесс содержит дискретные составляющие, то спектральные плоскости будут иметь особенности типа дельта функций. Пусть одномерный процесс состоит из стационарной последовательности некоррелированных импульсов, продолжительность которых стремится к нулю, а величина остается конечной. Корреляционная функция такого процесса выражается через дельта функцию δ(t), а спектральная плотность постоянна на всей частоте оси:
K(τ)=s.δ(τ), S(ω)= 
(1.10)
Такой процесс называется дельта-коррелированным, а постоянная s в формулах (1.10) интенсивностью белого шума. Корреляционная функция белого шума принимает в нуле бесконечное значение, т.е. дисперсии процесса не существует. «Белый» шум представляет собой все же чрезмерную абстракцию, поскольку его полная мощность, пропорциональная интегралу
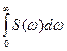(1.11)
оказывается бесконечно большой. Чтобы мощность процесса оставалась конечной, вводится ограничивающая частота ω.
Более реальной моделью будет усеченный «белый» шум спектральная плотность которого постоянна на отрезке и равна нулю вне этого отрезка.
