Рассмотрим собственные колебания прямоугольной в плане упругой пластинки со сторонами а и b и постоянной толщиной h (Рисунок 2.1).
Рисунок 2.1 – Схема колебаний прямоугольной
пластины с жестким защемлением.
Условия на контуре пластины будем пока считать произвольными. Уравнение колебаний пластинки имеет вид [4,9,10]
(2.1)
где ω(х, у, t) — нормальный прогиб, D — цилиндрическая жесткость ρ — плотность материала пластинки.
Подстановкой
ω(x,y,t)=W(x,y)eiωh
где ω — частота собственных колебаний, уравнение (2.1) приводится к виду:
(2.2)
Рассмотрим выражение
(2.3)
где f, х0, у0, λx, λy — некоторые константы. Это выражение удовлетворяет уравнению (2.2) и соответствует частоте
(2.4)
но не удовлетворяет граничным условиям. Для подчинения этим условиям мы располагаем лишь чётырьмя константами: f, х0, у0, λx, λy, так как f определяется из начальных условий. Как мы увидим ниже, при определенном выборе этих констант выражение (2.3) можно рассматривать как асимптотическое решение краевой задачи, соответствующее заданным условиям на контуре и справедливым при λx‹‹а, λy‹‹b в области, достаточно удаленной от контура пластинки.
Решение вблизи границы х = 0 будем искать в виде:
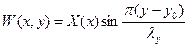(2.5)
Подстановка в уравнение (2.3) дает
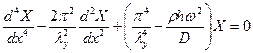
Соответствующее характеристическое уравнение
имёет два чисто мнимых и два действительных корня
, 
Здесь
(2.6)
Общий интеграл уравнения (2.5) имеет вид
В этом интеграле последний член, неограниченно возрастающий с увеличением х, должен быть отброшен. Первые два оставшихся члена полностью соответствуют асимптотическому представлению (2.3) для внутрённей области пластинки; первые три члена, взятые вместе, описывают динамический краевой эффект в пограничной зоне:
Пользуясь выражением (2.6) нетрудно оцёнить ширину области динамического краевого эффекта.
Учитывая, что С32~С12 + С22 можно считать, что, вклад последнего члена в выражение (2.1) оценивается множителем
Пусть х = λх. Тогда при βх=1 имеем 
. Даже в самом неблагоприятном случае (βх= 0) получается 
. Таким образом, ширина области динамического краевого эффекта не превышает длины полуволны.
Рассмотрим некоторые частные случаи граничных условий, положив в основу решение (2.6) для полностью защемленной стороны Х(0)=Х′(0)=0;
Отсюда
С2+С3=0, 
и следовательно
далее потребуем чтобы
(2.7)
Нетрудно видеть, что
, 
Окончательно получаем
(2.8)
Имея выражение (2.8), нетрудно найти изгибающие моменты в пластинке в зоне краевого эффекта. Поскольку изгибающий момент
(2.9)
то для линий, вдоль которых
получим
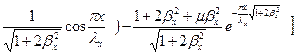(2.10)
Поведение прогиба и изгибающего момента в зоне краевого эффекта показано на рисунке 2.2 и 2.3. При вычислениях было принято что βх=1, μ=0,25.
Рисунок 2.2 – Схема поведения прогиба в зоне краевого эффекта
Рисунок 2.2 – Схема поведения изгибающего момента в зоне краевого эффекта. Штриховыми линиями показаны решения для внутренней области.
Рассмотрим более общий случай упругого защемления с коэффициентом жесткости с. Тогда:
,
функция Х (х) должна удовлетворять условиям;
X(0) = 0, 
Подставляя сюда выражение (2.6), получим
C2+C3=0
Отсюда
(2.11)
Из условия (2.7) найдем, что
(2.12)
При с→0 выражение (2.11) с коэффициентом (2.12) превращается в обычное решение для свободно опертой пластинки; при с→+∞ мы приходим к выражению (2.7).
Не будем останавливаться здесь на других случаях граничных условий, рассмотрение которых элементарно. В частности, можно построить решение, описывающее динамический краевой эффект вблизи подкрепляющего стержневого элемента, который сопротивляется изгибу и кручению.
Из изложенного следует, что для типичных краевых условий легко установить связь между максимальным напряжением σ в зоне краевого эффекта и амплитудой f колебаний во внутренней, области. Например, для заделанного края
(2.13)
Это соотношение соответствует некоторой паре длин полуволн λх, λу,: или некоторой паре волновых чисел m, n. В общем случае
(2.14)
где f mn— обобщенные координаты, характеризующие вклад каждой формы колебаний в движение пластинки, smn — коэффициенты динамического краевого эффекта.
До сих пор мы рассматривали задачу об исследовании динамического краевого эффекта при собственных колебаниях, полагая длины полуволн λх, λу известными. Покажем, как могут быть найдены эти величины и попутно частоты собственных колебаний пластинки.
Рассмотрим, например, прямоугольную в плане пластинку, защемленную. по всему контуру. Наряду с функцией Х(х), рассмотрим функцию
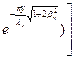
где β= λх/λу.
Выражение
удовлетворяет всем краевым условиям на границе у = 0 и при больших у приближается к,,внутреннему” решению (2.3).
Формы собственных колебаний прямоугольной защемленной по всему контуру пластинки распадаются на четыре группы по типам симметрии. Для первого типа (симметричные в обоих направлениях формы) должно быть
т.е.
, 
(2.15)
для второго типа (антисимметричные в обоих направлениях формы)
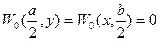
откуда
, 
(2.16)
два смешанных типа получим, комбинируя одно из условий из (2.15) с другим из (2.16).
Для каждого типа мы имеем систему двух уравнений с двумя неизвестными длинами полуволн λх, λу. Найдя эти величины, легко вычислить соответствующую собственную частоту (2.4).
Этот метод применим, строго говоря, лишь при условии, что λх<<а, λу<<b.
Вычисления показывают, однако, что он дает удовлетворительные решения даже для общей формы колебаний защемленной пластинки.
Рассмотрим вначале цилиндрический. изгиб (λу→∞, βх→0). Легко найдем, что
(m=1,2,…) (2.17)
Отсюда получаем формулу для собственных частот
(m=1,2,…) (2.18)
совпадающую с хорошо известной асимптотической формулой. При m= 1 точное решение дает в формуле для частоты числовой коэффициент 4,7302=22,373, в то время как асимптотическая формула (2.18) содержит коэффициент 3,1422. 1,5002 = 22,207 Разница составляет менее 1 %.
Применим тот же метод к квадратной пластинке а =b. При этом особенно простое решение получается для тех форм колебаний, у которых λх=λу
Тогда уравнения (2.15) и (2.16) принимают вид
, 
отсюда
(m=1,2,…)
причем нечетные волновые числа m соответствуют симметричным формам колебаний, четные — антисимметричным формам.
Собственные частоты определяются по формуле
(m=1,2,…) (2.19)
Рассмотрим теперь общий случай. Уравнения типа (2.15) и (2.16) легко могут быть сведены к одному уравнению, содержащему отношение βх= λх/λу
Это уравнение получается общим для всех четырех типов форм колебаний.
(m=1,2,…) (2.20)
где обратные тригонометрические функции понимаются в смысле главного значения. При больших m и n имеет место асимптотическая формула
(2.21)
для квадратной защемленной пластинки вычисления были сделаны Игути, который искал решение уравнение в виде ряда, удовлетворяющего условиям на контуре, и использовал прием, близкий к вариационному. Значения коэффициентов частоты α в формуле
найденные Игути, и значения, полученные асимптотическим методом, приведены в таблице. Расхождение по этим значениями невелико.
Таблица 2.1 – Сравнение значений коэффициентов частоты по Игути
и найденных асимптотическим методом
| m | n | βx | a/λx | a/λy | α | Расхождение % | |
| Данный метод | По Игути | ||||||
| 1,0000 | 4/3 | 4/3 | 3,556 | 3,646 | 2,53 | ||
| 2,0265 | 2,4372 | 1,2027 | 7,386 | 7,437 | 0,69 | ||
| 1,0000 | 7/3 | 7/3 | 10,889 | 10,965 | 0,70 | ||
| 3,0375 | 3,4688 | 1,1420 | 13,337 | 13,396 | 0,42 | ||
| 1,5079 | 3,4012 | 2,2556 | 16,656 | 16,717 | 0,37 | ||
| 1,0000 | 10/3 | 10/3 | 22,222 | - | - | ||
| 4,0432 | 4,4816 | 1,1084 | 21,313 | - | - | ||
| 2,0132 | 4,4366 | 2,2038 | 24,540 | 24,631 | 0,36 | ||
| 1,3370 | 4,3822 | 3,2784 | 29,960 | - | - | ||
| 1,0000 | 13/3 | 13/3 | 37,556 | - | - |
