Рис.6.8. кулачковый механизм с поступательно-вращающимся плоским толкателем.
Рис.6.9.диаграмма пути плоского толкателя в функции угла поворота кулачка.
Пусть прямая a-a образует с направлением движения звена 2 постоянный угол передачи 
(рис.6.8)
Для кулачковых механизмов данного вида должно удовлетворяться дополнительное условие, чтобы профиль кулачка был всегда выпуклым, т.к. его профиль есть огибающая кривая к положениям прямой a-a. Для этого будет показано ниже, необходимо, чтобы значения 
, величины 
, представляющей собой сумму наименьшего радиуса 
кулачка и перемещения 
звена 2, т.е. 
, 
, 
, …, были в каждом положении больше второй производной величины по углу поворота 
, взятой со знаком “-”, а это значит, больше аналога ускорения:
,
т.е.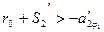 
, 
,
где 
и 
- текущие значения функции перемещения 
Это можно установить из следующих соображений. Пусть центр кривизны соприкасающегося участка профиля в рассматриваемом положении находится в т. B (рис.6.8) Строим заменяющий механизм ABCD и при точке B(
) строим план ускорений. Отрезок (
) представляет собой аналог 
ускорения 
звена 2 в рассматриваемом положении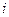 
механизма, т.е.
(6.16)
Таким образом, радиус кривизны 
профиля кулачка 1 в точке соприкасания C равен
(6.17)
где 
принимает последовательно значения 
,…. Кулачок 1 будет выпуклым, если центр кривизны его профиля в каждом положении будет удовлетворять условию
(6.18)
или
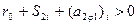(6.19)
откуда получаем
(6.20)
Разделив правую и левую части неравенства (6.20) на величину 
, получим
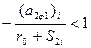(6.21)
или
(6.22)
Условие (6.22) позволяет провести следующее графическое построение (рис.6.10) для удовлетворения условия выпуклости профиля кулачка.
Рис.6.10 К определению минимального радиуса профиля кулачка с поступательно движущимся плоским толкателем.
По заданной диаграмме строим диаграмму 
(рис.610) Для этого производим разметку перемещений звена 2 по оси 
и откладываем на проведённых горизонтальных прямых значения 
. Соединив полученные точки плавной кривой, получим диаграмму 
.
Далее в той части диаграммы, которая соответствует отрицательным и максимальным по абсолютной величине значениям 
, проводим под углом 
к оси 
касательную 
к кривой . Согласно неравенству (6.22) центр вращения кулачка должен быть расположен ниже точки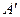 
. Если центр кулачка расположен в т. 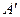, то неравенство (6.22) соблюдается. В самом деле, касательная 
к кривой в отрицательной части диаграммы 
, проведённая из т. А, составляет с осью угол, меньший . Выбрав центр вращения А кулачка, мы определим и величину минимального радиуса кулачка, равного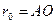 
, после чего построение профиля кулачка с выпуклым контуром не представит затруднений.
