Напряжения при растяжении (сжатии) Призматических стержней. Расчет на прочность * (* -нумерация рисунков – в рамках данного раздела)
Переходя к изучению введенных основных видов деформации стержней, ограничимся рассмотрением стержней постоянного поперечного сечения с прямолинейной осью, т. е. призматических стержней. Начнем с деформации растяжения (сжатия).
Напомним, что под растяжением (сжатием) понимают такой вид деформации стержня, при котором в его поперечном сечении возникает лишь один внутренний силовой фактор — продольная сила N z. Поскольку продольная сила численно равна сумме проекций, приложенных к одной из отсеченных частей внешних сил на ось стержня (для прямолинейного стержня она совпадает в каждом сечении с осью Oz), то растяжение (сжатие) имеет место, если все внешние силы, действующие по одну сторону от данного поперечного сечения, сводятся к равнодействующей, направленной вдоль оси стержня (рис. 1). Одна и та же продольная сила Nz при действии на различные части стержня (левую или правую) имеет противоположные направления. Знак Nz зависит от характера вызываемой ею деформации. Продольная сила считается положительной, если вызывает растяжение элемента (рис. 2, а), и она отрицательна, если вызывает сжатие (рис. 2, б).
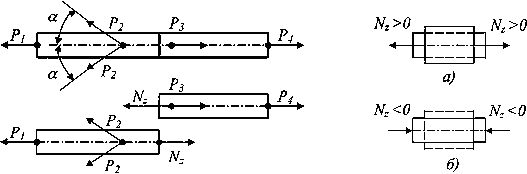
| Рис.1. Расчетная схема | Рис.2. а) Растяжение и б) сжатие |
Для того, чтобы сформулировать предпосылки теории растяжения (сжатия) призматического стержня, обратимся к эксперименту. Представим себе стержень, изготовленный из какого-либо податливого материала (например, резины), на боковую поверхность которого нанесена система продольных и поперечных рисок (рис. 3, а). Эта ортогональная система рисок остается таковой и после приложения растягивающей нагрузки (рис. 3, б). Поскольку поперечные риски являются следами поперечных сечений на поверхности стержня и остаются прямыми и перпендикулярными к оси стержня то это свидетельствует о выполнении гипотезы плоских сечений (Бернулли). С учетом гипотезы об отсутствии поперечного взаимодействия продольных волокон приходим к выводу, что деформация растяжения стержня сводится к одноосному растяжению его продольных волокон, и в поперечном сечении стержня возникают лишь нормальные напряжения а (рис. 4), индекс г у которых опускаем. Ортогональность продольных и поперечных рисок свидетельствует также об отсутствии сдвигов, а, следовательно, и связанных с ними касательных напряжений т в поперечных и продольных сечениях стержня.
Тогда продольная сила Nz равная сумме проекции внутренних сил, действующих в данном поперечном сечении площадью F (рис. 4) очевидно будет равна
.
Это соотношение является уравнением равновесия статики, связывающим продольную силу Nz, и нормальное напряжение 
, которое в общем случае является функцией координат х и у и поэтому не может быть найдено из одного лишь 1 уравнения статики. Таким образом, задача определения напряжений даже в самом простом случае деформирования стержня (растяжении или сжатии) оказывается статически неопределимой.
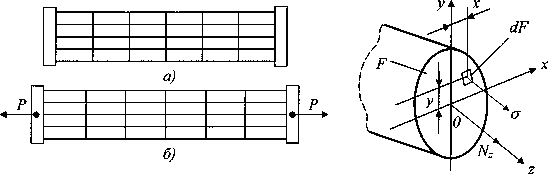
| Рис.3.Модель растянутого стержня | Рис.4. Связь напряжения и усилия |
Необходимое для решения этой задачи дополнительное уравнение вытекает из гипотезы плоских сечений. Поскольку поперечные сечения стержня, оставаясь плоскими и перпендикулярными к оси стержня, в процессе деформирования лишь поступательно перемещаются вдоль оси стержня (что приводит к одинаковому удлинению всех продольных волокон), то приходим к уравнению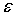 
=const, из которого ввиду однозначности связи и 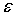(для линейно-упругого материала это—закон Гука: 
.) вытекает, что
Решая совместно уравнения получим, что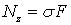 
или
Таким образом, при растяжении (сжатии) призматического стержня нормальные напряжения равномерно распределены по поперечному сечению, а касательные напряжения в сечениях отсутствуют, что является следствием гипотезы плоских сечений. Указанное, несмотря на, казалось бы, очевидность и простоту, является фундаментальным результатом, справедливым, строго говоря, лишь для призматического стержня. Однако в инженерной практике его используют и для приближенной оценки нормальных напряжений в стержнях переменного сечения. При этом, чтобы погрешность формулы была невелика, необходимо, чтобы площадь поперечного сечения стержня изменялась достаточно плавно вдоль его оси.
Условие прочности при растяжении (сжатии) призматического стержня для стержня из пластического материала (т. е. материала, одинаково работающего на растяжение и сжатие) будет иметь вид:
|
где 
—допускаемое напряжение. Напряжение в условии (А) подставляется по модулю, так как знак в этом случае роли не играет. Для стержней из хрупких материалов, неодинаково сопротивляющихся растяжению и сжатию, знак напряжения имеет принципиальное значение, и условие прочности приходится формулировать отдельно для растяжения и сжатия
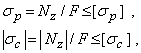
где 
и 
—напряжения растяжения и сжатия, а 
и 
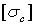— соответствующие им допускаемые напряжения.
В практике инженерных расчетов, исходя из условия прочности, решаются три основные задачи механики материалов конструкций. В применении к случаю растяжения (сжатия) призматического стержня эти задачи формулируются следующим образом.
Проверка прочности (поверочный расчет). Этот расчет проводится, если нагрузка (в нашем случае ее представляет Nz), сечение стержня F и его материал заданы.
Необходимо убедиться, что выполняется условие прочности
Проверочный расчет заключается в том, что определяется фактический коэффициент запаса прочности п и сравнивается с нормативным коэффициентом запаса [ n ]:
где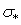 
— предельное (или опасное) напряжение, т. е. напряжение, вызывающее отказ элемента конструкции (напомним, что, например, для стержня из пластичного материала это—предел текучести 
или условный предел текучести 
).
Подбор сечения (проектный расчет). В этом расчете по Заданной нагрузке (Nz) определяются размеры поперечного сечения стержня (F) из заданного материала ( дано). Минимальное значение F получим, если в условии прочности (1) принять знак равенства:
Определение допускаемой нагрузки, то есть максимального значения нагрузки, которое допускает данный элемент конструкции (F и даны) при выполнении условия прочности.
Расчет валов
Рассмотрим расчет вала на прочность и жесткость. Пусть известна мощность W (кВт), передаваемая вращающимся с заданным числом оборотов в минуту (n) валом от источника мощности (например, двигателя) к ее потребителю (например, станку), а момент т, передаваемый валом, требуется найти, так как численно равный этому моменту крутящий момент необходим для расчета вала.
Если число оборотов вала в минуту n и соответствующая угловая скорость 
(с-1) постоянны, а Ф — угол поворота вала в данный момент времени t, то работа вращательного движения А=тФ. Тогда передаваемая валом мощность будет равна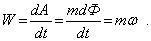 
Отсюда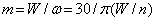 
кНм, где учтено, что 
.
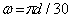Если мощность подается на вал через ведущий шкив, а раздается потребителям через несколько ведомых шкивов, то соответственно определяются моменты на шкивах, а затем строится эпюра крутящих моментов. Расчет вала на прочность и жесткость ведется по max Mz.
Определение диаметра вала из условия прочности. Для условия прочности при кручении вала допускаемые напряжения [τ] принимаются пониженными по сравнению с допускаемыми напряжениями обычного статического расчета в связи с необходимостью учета наличия концентраторов напряжений (например, шпоночных канавок), переменного характера нагрузки и наличия наряду с кручением и изгиба вала. Требуемое значение Wp=dз/16 получаем учитывая, что 
откуда получаем формулу для диаметра вала кругового сечения
|
Определение диаметра вала из условия жесткости. Условие жесткости состоит в наложении ограничения на погонный угол закручивания вала 
, так как недостаточно жесткие валы не обеспечивают устойчивой передачи мощности и подвержены сильным колебаниям:
|
Учитывая, что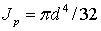 
, из условия жесткости получим:
|
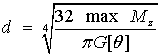
Список литературы.
1. Беляев Н. М. Сопротивление материалов. М., 1976. 663 с.
2. Писаренко Г. С. Сопротивление материалов. Киев: Выща шк. 1986. 775 с.
3. Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк. 1989. 624 с.
4. Пособие к решению задач по сопротивлению материалов/ Миролюбов И. Н. и др. М.: Высш. шк. 1974.
5. Расчеты на прочность и жесткость при растяжении (сжатии): метод. указания/ Ижевск: Изд-во Удм. ун-та; сост.: Б.Н. Шульга, В.В. Пряхин, А.Н. Воробьев. 2001. 36 с.
6. Расчеты на прочность и жесткость при кручении: Метод. указания/ Ижевск: Изд-во Удм. ун-та; сост.: Б.Н. Шульга, В.В. Пряхин, А.Н. Воробьев, 2001. 27 с.
7. Ицкович Г. М., Минин А. С., Винокуров Г. А., Руководство к решению задач по сопротивлению материалов, – М.: Высшая школа, 1999, 592 с.
ский. Ижевск, 1989.
Приложение 1
Механические характеристики материалов
| Материалы | sТ (s0,2), Мпа | sвр, sвс. Мпа | |
| Растяжение | Сжатие | ||
| 1. Сталь 3 2. Сталь 5 3. Сталь 20 4. Сталь 30 5. Сталь 40 6. Сталь 45 7. Сталь 50 8. Сталь 40, закаленная 9. Сталь 45, закаленная 10. Сталь 50 ХФА, закал. 11. Сталь 50 ХГР, закал. 12. Чугун СЧ12-28 13. Чугун СЧ15-32 14. Чугун СЧ21-40 15. Чугун СЧ24-44 16. Чугун СЧ32-52 17. Чугун СЧ35-56 18. Чугун СЧ38-60 | - - - - - - - | - - - - - - - - - - - | - - - - - - - - - - - |
Приложение 2
ГОУВПО «Удмуртский государственный университет»
РАСЧЕТНО-ПРОЕКТИРОВОЧНАЯ РАБОТА
по сопротивлению материалов
«Расчеты брусьев на прочность и жесткость
при растяжении (сжатии)»
Вариант № 5764
Выполнил студент гр. 17-31 А. В. Смирнов
Проверил к.т.н., доцент А.А. Семенов
Ижевск 20__
СОДЕРЖАНИЕ
Предисловие – 3
Введение - 4
Порядок выдачи и приема расчетно-проектировочных работ - 4
Общие указания по выполнению и оформлению РПР - 5 Основные понятия - 7 Расчеты валов на прочность и жесткость при кручении - 10
Вопросы и задания для самопроверки - 31
Варианты расчетно-проектировочной работы по расчету вала на прочность и жесткость при кручении (варианты А и Б) - 32
Прочность и перемещения при центральном растяжении или сжатии - 40 Список литературы - 44
Приложение 1 Механические характеристики материалов - 45
Приложение 2 Титульный лист - 46
Составители:
Александр Иванович Карманчиков – кандидат педагогических наук, заведующий кафедрой общеинженерных дисциплин Института гражданской защиты ГОУВПО «Удмуртский государственный университет».
Василий Васильевич Пряхин – кандидат технических наук, доцент, заведующий кафедрой общетехнических дисциплин НОУВПО «Камский институт гуманитарных инженерных технологий»
Методическое пособие по выполнению расчетно-проектировочной работы по курсу «Сопротивление материалов»
Печатается в авторской редакции
Подписано в печать 03.02.10.
Формат 60х841/16. Усл.печ.л. 2,8.
Уч.-изд.л. 2,6. Тираж 50 экз.
Типография «Удмуртский университет»
426034, Ижевск, Университетская, 1, корп. 4.
